Тема №2. Общая теория систем излучателей.

Пусть имеется некоторая дискретная система (набор дискретных излучателей) расположенных произвольным образом в пространстве. Определить поле в точке Р.

В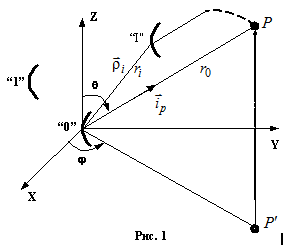 законы электродинамики все параметры входят в первой степени, значит они линейны, следовательно, принцип суперпозиции применим. Разобьем антенну на элементарные излучатели, тогда поле в точке Р.

Поле центрального излучателя:

Соответственно поле i-го излучателя:

Комплексная векторная ДН определяется:

Т.к. источники идентичны то и их ДН идентичны:

Т.о. поле в точке наблюдения можно записать:

А так как поле мы рассматриваем в дальней зоне, то (справа из прошлой темы).

Проанализируем выражение(6) преобразованное с учетом (5) и (7):

-множитель системы.

Правило перемножения диаграмм(правило Бонч-Бруевича)

Проведем математические преобразования:

(8) - амплитудное распределения в системе токов или полей. -фазовое распределение токов или полей.

Мы можем записать:

Соответственно:

Отсюда и вытекает правило перемножения диаграмм. Если нам необходимо определить ДН системы дискретных излучателей мы должны взять ДН центрального излучателя и умножить на множитель системы. Условия применения: идентичные излучатели, одинаково ориентированы, одна поляризация.

Физический смысл множителя системы - состоит в том, что он описывает пространственную, интерференционную картину излучения(комплексную ДН), системы изотропных излучателей с тем же амплитудно-фазовым распределением что и в антенне.

Г рафическая интерпретация правила перемножения диаграмм.

Результирующая ДН изображена пунктиром.

В основном ДН определяет множитель системы.

При перемножении не должно быть чтобы макс множителя системы совпадал, с мин ДН центрального излучения.

Множитель системы линейной дискретной системы с равномерным амплитудным и линейным фазовым распределением.

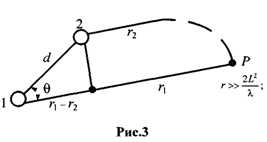Рассмотрим модель из двух излучателей. Дальняя зона. Внизу справа критерии дальней зоны.

Из определения cos:

Подставим в (9)

Равномерное амплитудное распределение, =1.

Линейное фазовое распределение(N- количество излучателей в системе)

С учетом количества излучателей:

А с учетом обозначении(14) и =1:

-начальная фаза. Обозначим Используем формулу геометрической прогрессии. Выполнив преобразования:

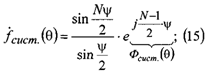
-фазовое распределение в системе(фазовая диаграмма решетки).

В общем случае нас интересует модуль:

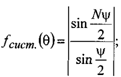Вводится обобщенны угол следовательно множитель системы преобразуется( - обобщенный угол):

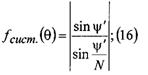
Анализ множителя линейной дискретной системы

-разность фаз между токами возбуждающие соседние излучатели. -разность хода лучей от соседних излучателей в точку наблюдения. -разность фаз полей обусловленная разностью хода волн.

Будем считать что:

Найдем множитель системы максимальный:

получаем неопределенность 0/0, разрешим ее переходя к предельному соотношению, синусы заменим на аргументы.

Нормированный множитель системы:

Выясним какие направления имеют максимальные и минимальные значения. Из (18) следует:

1. множитель система функция периодическая с периодом 2п, это же следует из анализа обобщенного угла.

2. Если разность фаз полей приходящих в точку наблюдения от любых двух соседних излучателей кратна 2п то в этих направлениях формируется максимум множителя системы.

Максимальное направление:

Направление главного максимума всегда определяется выражением (19).

Замечание:

1)Выражение (19) справедливо для любых амплитудных распределений.

2)Анализ (19) показывает, что в направлении формируется ряд одинаковых по величине максимумов. Максимум который соответствует называют главным(центральным) максимумом. Остальные называют дифракционными.

3)Между соседними главными максимумами существует нолей и боковых лепестков

-направление нолей.

-направление боковых лепестков.

Уровень боковых лепестков:

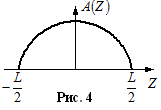
При равномерном Амплитудном распределении уровень боковых лепестков самый большой и составляет 21%=-13.3дБ. Ширина главного kbgtcnrf ДН определяется(N-количество излучателей, d-расстояние между ними):

Чтобы сузить главный луч ДН можно увеличит количество излучателе либо расстояние между ними.

Рис 4

Запитка синфазная, отличается только фазовый множитель. Т.к. электромагнитную энергию лучше передавать одним лепестком (лучше помехозащищенность и скрытность, электромагнитная совместимость). Считаем что антенна является синфазной(каждый элемент запитан в одной фазе). Получим условие единственности главного лепестка в виде:

Замечание:

Максимум излучения идет по нормали(так как элементарный вибратор). Если учитывать угол от оси решетки к нормали то будет cos если наоборот то sin.

А нализируем поле в точке P. Разность хода будет:

Условие единственности главного лепестка.

Рассмотри размеры рабочей области, в общем случае: (оласть реальных урлов) должен лежать в таких пределах; (н-начала, к-конца) Отсюда:

Рассмотри рисунок(тоже что и рис 4), но рабочая зона смещена из за несинфазной запитки.

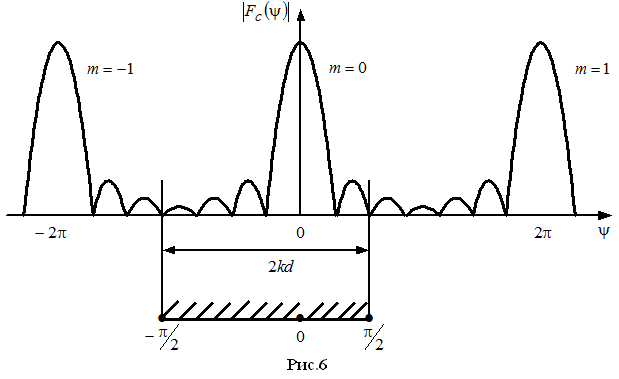
Меняя фазовое распределение обеспечивается сканирование лучом ДН в пространстве. При сканировании ДН область рабочих углов смещается, а в области реальных углов ДН смещается. Не нарушим ли мы условие единственности лепестка, и что мы должны учитывать при вращении ДН в пространстве. Будем исходить из условия ед гл лепестка

Учитываем излучатели:

Соответственно условие ед. гл. лепестка при сканировании:

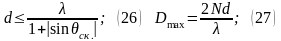
Пример: Построим множитель системы . Построим числитель: Функция периодическая, а так N=4, то построим 4п, амплитуда соответственно . График ниже знаменателя синусоида расширенная в 4 раза. Дальше третий график числитель разделим на знаменатель ,неопределенность 0/0 дает максимум. Затем считаем вещественный угол. Далее рисуем максимум главного луча, и боковые лепестки. Самый нижний рисунок при не синфазной запитке.

Линейная непрерывная система излучателей с равномерным амплитудным и линейным фазовым распределением.

Рассмотри обычный симметричный вибратор.

Разобьем на элементарные излучающие участки. Чтобы определить поле в дальней зоне

ДН определим по правилу перемножения диаграмм, множитель системы запишем как у дискретной системы излучателей.

Из дискретной получим непрерывную систем, рассмотрев предельное соотношение(аналогично для фазового и амплитудного распределения):

(5)Множитель непрерывной системы излучателей для любого амплитудного и фазового распределения.

Множитель системы синфазной равномерно возбужденной антенны

( преобразование по формулам Эйлера)

- Нормированный множитель системы)

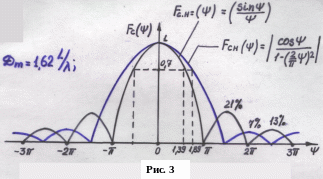
Из графика видно что ноли ДН определяются: Направление и уровень БЛ определяются соответственно:

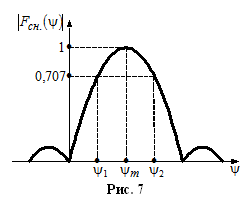
Ширина ДН определяется по уровню половинной мощности из условия:

или решая это трансцидентное уравнение и пользуя таблицей , получим перейдя к реальным углам , а поскольку L>>

Множитель системы синфазной линейной антенны с симметричным амплитудным распределением

Вычислим интеграл (16) с учетом и нормируя получим:

график на рис.3. Анализируя амплитудное и косинусоидальное распределения мы видим: произошло расширение гл. луча ДН и уменьшение уровня БЛ.

Решая это трансцидентное уравнение и пользуя таблицей , получим:

В общем виде амплитудное распределение можно представить в виде:

Пример:

Нормированный множитель системы:

Таблица №1

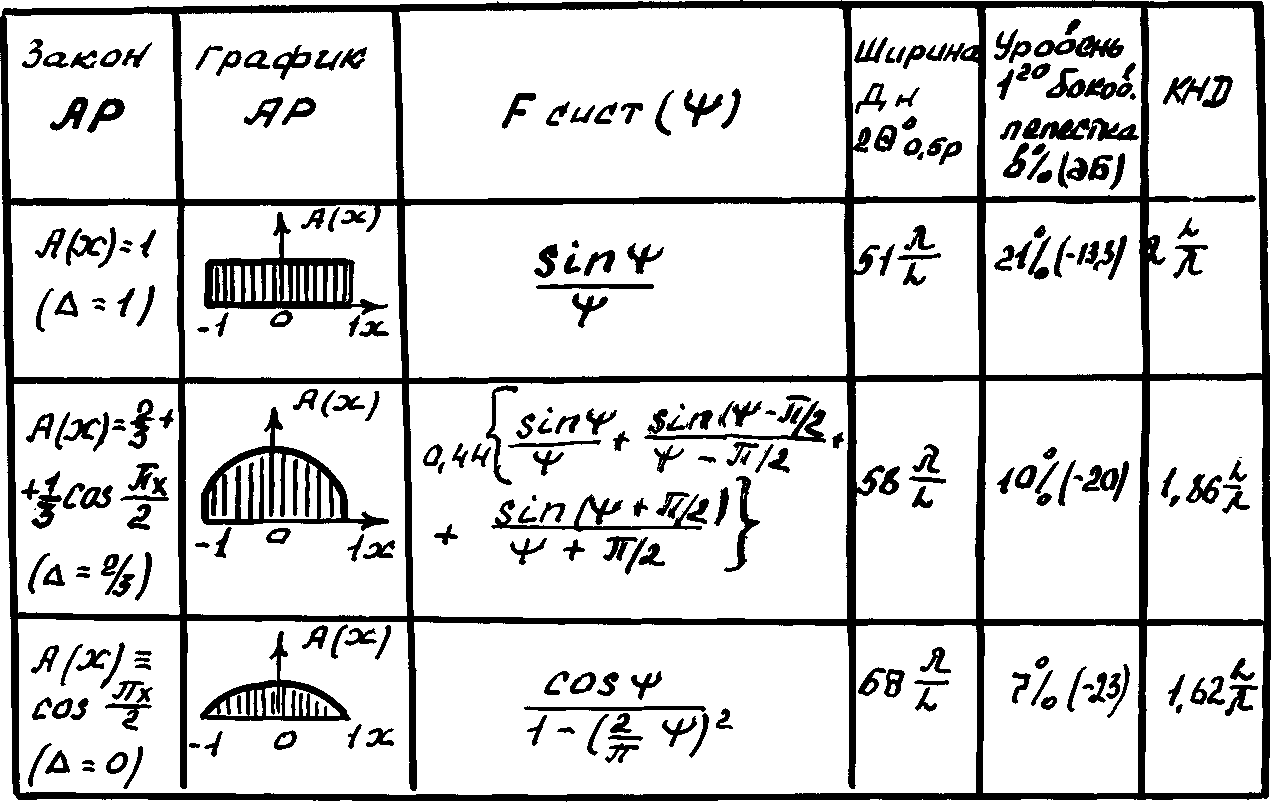
Существует еще биномиальная ДН, ее характеристики гораздо лучше, чем у приведенных в таблице 1, но реализовать на техники ее на технике не удалось. Активно используется оптимальное амплитудное распределение (Дольф-Чебышевское), сочетает и узкую ДН и приемлемых уровень БЛ.

При косинусоидальном распределении мы можем антенну разбить, на множество элементарных антенн с равномерным амплитудным распределением, одна антенна короче другой, то ширина ДН будет увеличиваться, в связи с уменьшение действующей длины антенны, уровень бок лепестков будет уменьшаться.

Ниже построим множитель системы(1 соответствует 1, n-n), для самой длинной антенны самая узкая ДН и самый высокий уровень, для самой короткой антенны наоборот. В итоге боковые лепестки компенсируют друг друга, в результате при косинусоидальном распределений получаем небольшой уровень БЛ.

Рассмотрим линейное фазовое распределение:

Фазовое распределение представим в виде степенного ряда:

Квадратичное и кубичное фазовое распределение используется редко, обычно используется, линейное.

Рассмотрим множитель системы, подставим

Антенна от 1 до -1, линейное фазовое распределение - определяет скорость нарастания. Множитель системы в обобщенных углах, сдвинут на величину .

О тсюда:

М ножитель системы в обобщенных углах сдвинулся, в полярных координатах, сместившись на величину опустим перпендикуляр, то увидим, что действующая длина уменьшилась, следовательно будет расширяться гл. луч ДН, нарушение симметрии, расширяться, будет больше в ту сторону в которую отклоняется данный луч. Что отражено и в реальных углах на рис. 9

Т.о, мы видим что обобщенных углах нет нарушения симметрии, а в реальных есть.

(Рис 10а)- вращаем без сканирования получается тор, а если будем вращать со сканирующим лучом(Рис 10а) то будем наблюдать свертывание ДН в форму воронки, это снижает точность определения координат.

С истема излучателей, расположенных в плоскости.

Большинство антенн характеризуется излучателями, расположенными в плоскости.

Рассмотрим систему излучателей расположенных в плоскости, элементарная излучающая площадка dS(источник Гюйгенса).

Определим множитель системы. Применим теорему перемножения диаграмм.

Так площадь произвольная то множитель системы: учтем что:

Тогда ДН:

-площадь раскрыва антенны.