1.5.1. Метод контурных токов (метод Максвелла)

Суть метода заключается в следующем. Выбираются независимые контуры (не перекрывающие друг друга) и направления контурных токов в них. Записывается и решается система k алгебраических уравнений в соответствии со вторым законом Кирхгофа для каждого контура (k-число контуров):

…………………………………..

…………………………………..

где - сумма сопротивления ветвей, входящих в контур;

- Алгебраическая сумма ЭДС, включённых в ветви, образующих контур n.

Определяются токи ветвей как алгебраические суммы (разности) соответствующих контурных токов:

1.5.2. Метод двух узлов

Метод двух узлов используется для цепей, имеющих n ветвей два узла аи b (например, цепь, представленная на рис. 1-1). Узловое напряжение определяется по формуле:

, В,

где - Алгебраическая сумма произведения ЭДС ветвей на проводимости этих ветвей;

- сумма проводимостей всех ветвей, соединяющий узел аи b

1.5.3. Метод наложения

Ток в любой ветви может быть рассчитан как алгебраическая сумма токов, вызываемых в ней от ЭДС каждого источника напряжение в отдельности. При расчёте токов, вызываемых каким либо источником ЭДС , другие источники ЭДС замыкаются накоротко.

1.5.4.Метод эквивалентного генератора

Для определения тока I в произвольной ветви ab с сопротивлением r. Нужно разомкнуть эту ветвь и часть цепи, подключенную к этой ветви заменить эквивалентным генератором ЭДС и внутренним сопротивлением . Расчёт ведётся любым известным способом. Расчёт ведут пологая, что оно равно входному сопротивлению цепи с закороченными источниками ЭДС относительно ab. Определяют токи в искомой ветви:

, А.

1.5.5. Преобразование сложных цепей в простые эквивалентные

Замена n последовательно соединённых сопротивлений эквивалентным:

, Ом.

Замена n соединенных сопротивлений эквивалентным:

, Ом.

Переходя к проводимостям получим:

, См.

Эквивалентное сопротивление при смешанном соединении сопротивлений складывается из суммы последовательно соединённых сопротивлений и эквивалентного значения параллельных соединённых.

Преобразование треугольника сопротивлений (рис.1.4, а) в эквивалентную звезду (рис.1.4, б) и обратное преобразование.

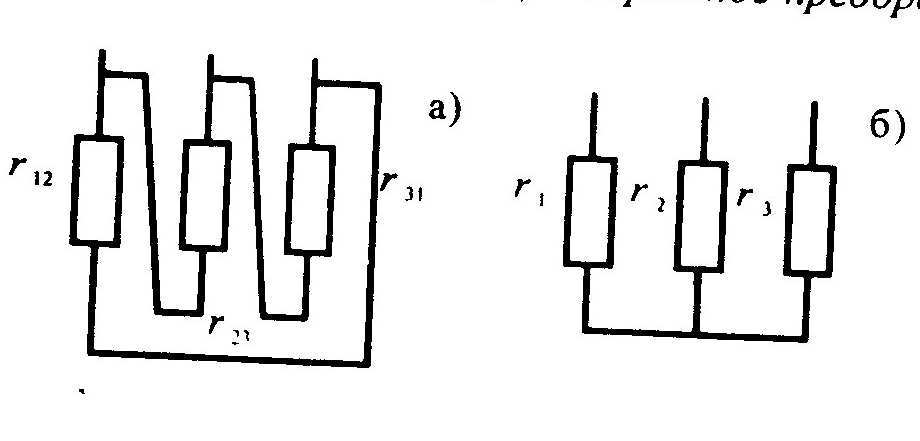
1.5.6. Баланс электрических мощностей цепи

Для любой замкнутой цепи сумма мощностей источников электрической энергии равна сумме мощностей , расходуемых в приёмниках энергии:

, или , Вт.

Где n – число источников электрической энергии

m – число приёмников электроэнергии.

1.6. Переходные процессы в цепях постоянного тока

В общем случае для цепи, содержащей источник ЭДС , сопротивления индуктивности , взаимоиндуктивности и ёмкости С для определения искомого тока записывают линейное однородное дифференциальное уравнение в соответствии со вторым законом Кирхгофа для данного контура:

.

Ток, являющийся общим решением этого уравнения представляют ввиде двух составляющих:

где - свободный ток – составляющая, действующая лишь в переходном режиме,

- вынужденный ток – составляющая действующая в установившемся режиме.

Ток получают, как частное решение этого уравнения со свободным членом при

Ток получают как общее решение уравнение без свободного члена.

Приведём примеры решения для некоторых типовых цепей.

А) Включение цепи, содержащей последовательно соединённые резистор сопротивление r и индуктивность L, на постоянное напряжение U (рис.1.5):

, или (а-1)

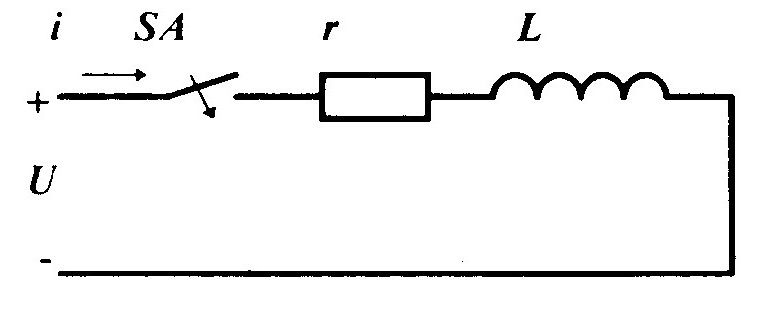
Вынужденная составляющая тока:

(а-2)

Уравнение без свободного члена:

(а-3)

Его характеристическое уравнение:

(а-4)

Общее решение уравнения (а-3)

Общее решение уравнения (а-1)

(а-5)

Постоянную А находят из (а-5), пологая при t=0 ; :

Решение уравнения (а-1):

(а-6)

Б)при включении цепи, содержащей последовательно соединённые резисторы с сопротивлением r и конденсатор С, на постоянное напряжение U (рис.1.7), её уравнение имеет вид:

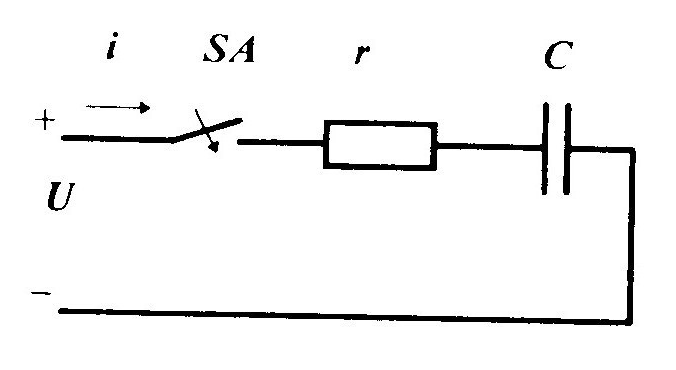
(б-1)

где: - ток в цепи, ,

U - падение напряжения на конденсаторе.

(б-2)

Решение (б-2) ищется в виде:

и (б-3)

Характеристическое уравнение для (б-2)

(б-4)

Свободная составляющая напряжения

(б-5)

Решение уравнения (б-2):

(б-6)

Поскольку в начальный момент времени, при , то

A=-U, следовательно искомое решение:

(б-7)

где - постоянная времени цепи.