
- •5 Линейные измерения
- •5.1 Способы линейных измерений
- •5.2 Непосредственное измерение расстояний
- •5.3 Измерение расстояний оптическими дальномерами
- •5.4 Измерение расстояний радио- и светодальномерами
- •6 Нивелирование
- •6.1 Способы нивелирования
- •6.2 Устройство нивелира
- •6.3 Поверки и юстировки нивелиров
- •6.4 Геометрическое нивелирование
- •6.5 Тригонометрическое нивелирование
- •6.6 Гидростатическое и барометрическое нивелирование
- •7 Основы математической обработки результатов измерений
- •7.1 Виды геодезических измерений
- •7.2 Классификация ошибок измерений
- •7.3 Оценка точности результатов измерений
- •8 Опорные геодезические сети
- •8.1 Классификация опорных геодезических сетей
- •8.2 Традиционные методы построения государственных геодезических сетей
- •8.3 Государственная геодезическая сеть
- •8.4 Современное состояние государственной геодезической сети. Новая единая система координат ск-95
- •8.5 Новая структура Государственной геодезической сети
- •9 Топографические съемки
- •9.1 Общие сведения о крупномасштабных топографических съемках
- •9.2 Съемочное обоснование
- •9.3 Горизонтальная съемка
- •9.4 Вертикальная съемка
- •9.5 Тахеометрическая съемка
- •9.6 Основы аэрофотосъемки и наземной фотосъемки
- •10 Основные виды геодезических работ при проектировании, строительстве и эксплуатации сооружений
- •11Инженерно-геодезические изыскания
- •12 Геодезическое проектирование
- •12.1 Понятие о генеральном плане сооружения
- •12.2 Геодезические расчеты при составлении генерального плана
- •12.3 Проектирование трасс линейных сооружений
- •12.4 Вертикальная планировка
- •13 Геодезические работы на строительной площадке
- •13.1 Расчет данных для выноса осей сооружения на местность
- •13.2 Элементы и способы разбивочных работ
- •13.3 Вынос и закрепление основных осей на дне котлована
- •13.4 Разбивка осей фундамента
- •13.5 Передача осей и высот на дно котлована и на монтажные горизонты
- •13.6 Исполнительные съемки на строительной площадке
- •14 Геодезические определения деформаций сооружений
- •14.1 Общие сведения о деформациях сооружений
- •14.2 Наблюдения за осадками фундамента сооружения
- •14.3 Определение горизонтальных смещений сооружений
- •14.4 Наблюдения за креном высотных зданий и сооружений
- •15 Геодезические работы при градостроительстве
- •15.1 Вопросы планировки и проектирования городов
- •15.2 Составление и расчеты проекта красных линий
- •15.3 Вертикальная планировка городской территории
- •15.4 Архитектурные обмеры
7.3 Оценка точности результатов измерений
Равноточные измерения
При выполнении измерений возникает задача отыскания наиболее надежного значения из ряда полученных в процессе измерений результатов. Примером подхода к решению такой задачи является анализ арифметического среднего.
Арифметическое среднее является наиболее надежным значением, если выполнен ряд измерений одной и той же величины. Пусть истинное значение равно Х, а l1, l2, l3, ..., l n - ряд измерений. Получим истинные ошибки:
1 = l1 - X, 2 = l2 - X, 3 = l3- X, . . ., n = l n - X. (75)
Найдем сумму уравнений истинных ошибок, которые будем считать случайными ошибками. Эта сумма равна [] = [l]-nX. Поделим ее на n. Получим [] / n = [l]/n -X. Но сумма случайных ошибок, деленная на число, стремится к нулю в соответствии со вторым свойством случайных ошибок, а [l]/n X, то есть при выполнении равноточных измерений арифметическое среднее стремится к истинному значению измеряемой величины. Это является подтверждением надежности среднего арифметического значения.
Для отыскания средней квадратической ошибки примем общую формулу ошибки функции ряда измеренных величин
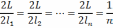 (76)
(76)
 (77)
(77)
Так как измерения равноточные, то m1 = m2 = = mn = m
Поэтому
 ,
,
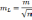 (78)
(78)
То есть ошибка среднего арифметического уменьшается в n раз по сравнению с ошибкой одного измерения.
Средняя квадратическая ошибка функции ряда измеренных величин
Предположим, что искомую величину F мы находим как функцию ряда измеренных величин
F = f (x, y, z...t)
где x, y, z...t - результаты измерений, содержащие ошибки.
В математике доказывается, что главный член приращения функции, зависящий от малых приращений аргументов равен полному дифференциалу этой функции, то есть
 (79)
(79)
 ,
,  ,
, 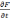 -
частные производные данной функции по
соответствующим аргументам.
-
частные производные данной функции по
соответствующим аргументам.
Предположим, что для искомой величины был выполнен бесконечно большее число циклов независимых измерений величин. Тогда для каждого цикла можно записать уравнение ошибок
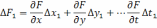

.
.
.
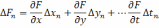
Чтобы избавиться от двойственности знаков у ошибок измерений, каждое из этих уравнений возведем в квадрат, затем сложим все уравнения и разделим на число измерений h. В итоге получаем
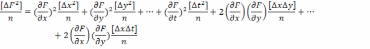
По четвертому свойству случайных ошибок последние, подчеркнутые, члены этой функции стремятся к нулю при неограниченном возрастании числа измерений. Поэтому средняя квадратическая ошибка функции ряда независимых измерений имеет вид (при независимых ошибках измерений)
 (80)
(80)
Вычисление средней квадратической ошибки одного измерения по отклонениям oт наиболее надежного значения
На практике истинные ошибки измерений обычно т неизвестны и вместо них приходится пользоваться отклонениями отдельных результатов измерений от наиболее надежного значения. Если измерения равноточные, то таким наиболее надежным значением будет среднее арифметическое L. Отклонения от среднего обладают единственным свойством, что их сумма всегда равна нулю, т.е. если
L = l / n и i = li – L, то = 0.
Имея величины можно вычислить и среднюю квадратическую ошибку одного измерения. Это следует из такого вывода. Пусть дан ряд равноточных измерений l1, l2...ln, x - истинное значение измерений величины, L - среднее, наиболее надежное значение.
Составим уравнения ошибок и уравнения отклонений
l1 – x 1 = l1 - L
2 l2 – x 2 = l2 - L
.................................................................
.................................................................
n ln – x n = ln - L
Составим последовательные разности уравнений и выразим истинные ошибки через отклонения
- 1 = L – x = 1 + (L - x)
2- 2 = L – x 2 = 2 + (L - x)
..............................................................................
...............................................................................
n- n = L – x n = n + (L - x)
Каждое из этих уравнений возведем в квадрат и сложим затем все уравнения
2= 12 + 21 * (L – x) + (L - x)2
22= 22 + 22 * (L – x) + (L - x)2
........................................................
........................................................
n2= n2 + 2n * (L – x) + (L - x)2
----------------------------------------------------
[2] = [v2] + 2 * (L – x) * [v] + n * (L - x)2
так как [] = 0, тo [2] = [v2] + n * (L - x)2
В свою очередь разность (L – x) представляет собой истинную ошибку среднего арифметического. Если замерять ее средней квадратической ошибкой, mL полагая, что mL = m / n L – x, то получим [2] = [v2] +m2 или

Решая последнее уравнение, получим
 или
или
 ,
,
 (81)
(81)
Эту формулу впервые вывел немецкий ученый Бессель, и она носят его имя.
Обработка результатов неравноточных измерений
Измерения, выполненные в разных условиях, называются неравноточными. При неравноточных измерениях степень надежности каждого измерения различна. Для ее характеристики введено понятие веса измерения. Весом называют величину обратно пропорциональную квадрату средней квадратической ошибки измерения.
Так каждый результат измерения можно оценить его ошибкой и весом.
l1 m1, вес p1 = 1/m12; l2 m2, вес p2 = 1/m22
При сопоставления весов, для удобства расчета их можно увеличить или уменьшить в одинаковое число раз.
Так p1 = с : m12; p2 = c : m22 (c = const)
Например, если среднее арифметическое определяется из разного числа n1 и n2 равноточных измерений
L1 = l / n1, mL12 = m2 / n1 , L2 = l / n2, mL22 = m2 / n2
p1 = n1 / m2, p2 = n2 / m2
где m - ошибка одного измерения, и если принять с = т2, то p1 = n1, p2 = n2 т.е. формально за вес простой арифметической средины можно принять число измерений, из которых она составлена. При определении искомой величины из ряда неравноточных измерений простое среднее арифметическое нельзя принять за наиболее надежный результат, так как к более точным измерениям нужно отнестись с большей степенью доверия. В этом случае нужно пользоваться формулой общей арифметической середины, вывод которой сделан на основе таких рассуждений.
Пусть дан ряд равноточных измерений, числом n
l1, l2....ln, L = l : n
Разобьем этот ряд на несколько неравных частей и из каждой его части составим свое среднее значение l/ эти значения уже будут неравноточными
l1 = l1 / n1, l2 = l2 / n2, l3 = l3 / n3, n1 + n2 + n3 = n
тогда можно записать

но l1 = l’1 * n1, l2 = l’2 * n2, l3 = l’3 * n3
а так как формально веса pi = ni то
 (86)
(86)
Эта формула называется формулой общей арифметической средины. Ею можно пользоваться и при равноточных измерениях, так как приняв в этом случае р = I, получим L1 = l / n 1 т.е. формула простой арифметической средины является частым случаем общей арифметической средины.
Пример. Один и тот же угол измеряется разными теодолитами результаты:
= 15°32 30, m1 = 20, p1 = 1/400
2 = 15°32 20, m2 = 10, p2 = 1/100
3 = 15°32 10, m3 = 5, p3 = 1/25
Пусть С = 400, тогда p1 = 1; p2 = 4; p3 = 16. Тогда вынося общую часть 15°32 за знак формулы, получаем

т.e. полученный результат, близкий к третьему точному результату измерений.
Найдем формулу веса общей арифметической средины
 (87)
(87)
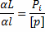 (88)
(88)
 (89)
(89)
но,

тогда mL2 = p/p2 = 1/p , а вес PL = 1/mL2 = p
Тo есть, вес общей арифметической средины равен сумме весов слагаемых
измерений.
Свойство отклонений V от общей арифметической средины.
Пусть дан ряд измерений l1...ln с весами p1...pn
L = l * p / p
Составим уравнения отклонений
l1 – L = V1 * p1 = p1* l1 – p1 * L = p1 * V1
l2 – L = V2 * p2 = p2* l2 – p2 * L = p2 * V2
....................................................................
ln – L = Vn * pn = pn* ln – pn * L = pn * Vn
p * l - L* p = p * V = 0
Понятие об ошибке измерений, вес которой равен единице (ошибка единицы веса).
При неравноточных измерениях вместо ошибки одного измерения определяется средняя квадратическая ошибка измерения, вес которой равен единице.
Если дан ряд измерений l1, l2...ln, с ошибками i и весами рi то можно записать пропорции




 то
то
 (90)
(90)
Если в ряде измерений получены отклонения V от общей арифметической средины, то
 это
обобщение формулы Бесселя
(91)
это
обобщение формулы Бесселя
(91)
Поэтому средняя квадратическая ошибка общей арифметической средины вычисляется по формуле
 (92)
(92)
Двойные измерения
В ряде случаев практики для определения искомых величин делают двойные измерения, например линии измеряют два раза, углы – два раза и т.п.
По разностям таких двойных измерений можно получить данные для оценки точности, если имеется ряд двойных измерений l1, l2...ln , l1, l2...ln , то
d1 = l1 – l1
d2 = l2 – l2
.................
dn = ln – ln
Эти разности di являются истинными ошибками измерений. Поэтому средняя квадратическая ошибка двойного измерения
 ,
а ошибка одного измерения
,
а ошибка одного измерения
 (93)
(93)
так как m2d = m12 + m22 2m2
Если в разностях d наблюдается преобладание членов со знаком + или знаком -, то это свидетельствует о наличии систематической ошибки, которую следует исключить. Для этого составляется средняя разность dср =d/n и вычисляются отклонения от среднего:
= d1 - dср , 2 = d2 - dср , ... n = dn - dср
И в этом случае ошибка одного измерения будет вычисляться по формуле
 (94)
(94)
Если измерения неравно точны, то применяются обобщенные формулы

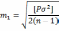 (95)
(95)
Понятие о методе наименьших квадратов
Как правило, все геодезические измерения выполняются в таком количестве, которое обеспечивает контроль измерений и дает возможность выполнить оценку точности. При производстве массовых геодезических работ, наиболее надежные результаты отыскивают для совокупности измеренных величин по принципу наименьших квадратов. Этот принцип, предложенный Гауссом и Лежандром предусматривает такое решение задачи, при котором сумма квадратов поправок к измеренным величинам будет минимальной. Такое решение будет самым надежным с вероятностной точки зрения.
Например, если отыскивать по этому принципу наиболее надежный результат "Х" из ряда равноточных измерений одной и той же величины, то потребуется определить минимум функции


Откуда
 ,
то есть получим формулу арифметической
средины.
,
то есть получим формулу арифметической
средины.
А
так как
 ,
то при значении Х
= l/n
= L
получим
минимум исходной функции.
,
то при значении Х
= l/n
= L
получим
минимум исходной функции.
Справедливость
принципа наименьших квадратов можно
показать и нa таком примере. Пусть в
треугольнике измеряют равноточные углы
и сумма углов оказалась равной 1800006,
f=
б".
Естественно предположить, что если
измерения выполнены равноточно, то
каждому углу нужно придать поправку
 тогда
= 12. Если невязку распределить неравномерно,
например
тогда
= 12. Если невязку распределить неравномерно,
например
V1 = -6; V2 =0; V3 = 0, то = 36
или
V1 = -1; V2 =-1; V3 = 4, то = 18.
Иначе говоря, если сумма квадратов поправок минимальна, то искомый результат будет по вероятности самым надежным, этот же принцип при неравноточных измерениях выражают соотношением
p*V2 = min.
Примеры
I) Сделать оценку точности ряда измерений некоторого отрезка x = 120.30м.
№ |
L, м |
∆=l-x,см |
∆2 |
1 |
120.28 |
-2 |
4 |
2 |
120.31 |
+1 |
1 |
3 |
120.34 |
+4 |
16 |
4 |
120.28 |
-2 |
4 |
5 |
120.33 |
+3 |
9 |
[∆2]=34

∆max=2m=5.2см


2) Площадь прямоугольника определяется по измеренным сторонам а и в; составить формулу для вычисления средней квадратической ошибки площади по известным ошибкам измерения сторон

 ,
,
 ,
,

Поэтому
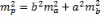
Из этой формулы следует, что для того, чтобы получить площадь фигуры более надежно, короткую сторону "В" нужно измерить точнее.
3) Превышение из геометрического нивелирования определяют по разности отсчётов по рейкам h = a – b. Найдя выражение для mh
Решение:
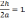 ,
,

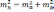
4) В замкнутом теодолитном ходе подсчитывается сумма углов для определения невязки.
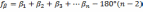
 ,
,

поэтому
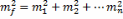 ,
и если углы измерены равноточно и
,
и если углы измерены равноточно и
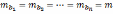 ,
то
,
то
 ,
а
максимальная невязка с вероятностью
,
а
максимальная невязка с вероятностью
β=0,95
,
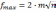
(сравните с допустимой угловой невязкой).
5) при вычислении горизонтальной проекции линии угол наклона измеряется эклиметром. Получены следующие данные измерений
S = 100,00м, ms = 0,1 м, = 30°, m = 0,5°
Вычислить среднюю квадратическую ошибку горизонтальной проекции
 ,
,
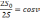 ,
,

Поэтому m2S0 = cos2 * m2s + s2 * sin2 * m2
(В последнем выражении ошибку угла m нужно выражать в радианной меpe, чтобы сохранить линейную размерность искомого результата)
m2S0 = ¾ * 100см2 + 108 см2 * ј * 0,25/(57,32) = 75 см2 + 2000см2 и ms = 45 см. Как видно из этого расчета ошибки измерения угла оказала большое влияние на погрешность искомого результата и поэтому эклиметром разрешается измерять углы наклона только до 7°.
6)
№ |
l, м |
|
V2 |
1 |
120,06 |
0 |
0 |
2 |
120,14 |
+8 |
64 |
3 |
120,04 |
-2 |
4 |
4 |
120,05 |
-1 |
1 |
5 |
120.01 |
-5 |
25 |
|
120,06 |
0 |
94 |
L=120.06 [v2]=94

[v]=0


∆max=2m=9.2см



