9 Топографические съемки

9.1 Общие сведения о крупномасштабных топографических съемках

После построения геодезических сетей на территории изучаемого объекта появляется координатное обеспечение, необходимое для построения модели объекта. Такими моделями для физической поверхности Земли являются топографические планы, профили и карты. Основным видом геодезических работ при создании модели физической поверхности является топографическая съемка, которая может быть определена как совокупность измерительных, вычислительных и графических операций, необходимых для получения топографического плана, профиля, карты земной поверхности.

Принцип от «общего к частному» предполагает выполнение измерений на местности в два этапа: создание съемочного обоснования и детальная съемка. Такой принцип организации работ позволяет избегать накопления ошибок измерений, и съемка ведется в единой системе координат. И, наконец, третьим заключительным этапом является вычислительная и графическая обработка полевых измерений, в результате которой и получается план или профиль участка местности.

По методам измерительных действий различают инструментальную съемку, когда информация о каждой точке местности получается при помощи прибора (теодолита, тахеометра, кипрегеля) измерением расстояний и углов. В зависимости от применяемых инструментов иногда называется инструментальная съемка - теодолитная, тахеометрическая, мензульная. Иногда съемка называется по методам представления информации о местности. В застроенной местности часто для определения планового положения точек объектов съемки осуществляются измерительные процедуры при помощи теодолита и мерной ленты или радиодальномера, которые называются горизонтальной съемкой. На некоторых территориях для съемки рельефа и определения высот точек технологических объектов коммуникаций применяется вертикальная съемка, осуществляемая методами геометрическог или тригоноетрического нивелирования.

Особым образом, рассматривается фотографическая съемка, при которой местность фотографируется либо с земли (наземная фототопографическая съемка), либо с воздуха (аэрофотосъемка). Полученные фотографии местности являются основным документом для построения модели местности.

Вычислительные работы, заключающиеся в обработке журналов измерений, составлении схем обоснования, вычислении координат точек съемочного обоснования, и графические работы - составление и вычерчивание планов для разных видов съемки во многом отличаются лишь средствами исполнения. Это может быть ручная обработка результатов съемки либо при помощи компьютера с использованием графических редакторов или специально составленных программ обработки результатов измерений.

9.2 Съемочное обоснование

Обычно съемочным обоснованием крупномасштабной съемки в условиях равнинной местности служат теодолитные ходы – полигонометрия низшего класса, а в пересеченной – сети микротриангуляции с короткими сторонами.

Теодолитным ходом называют замкнутый или разомкнутый многоугольник на местности, в котором измерены все стороны и углы. Для выполнения работ в заданной системе координат эти ходы привязывают к пунктам высшего класса.

Различают три вида теодолитных ходов: замкнутые, разомкнутые и висячие (Рисунок 65).

Для обеспечения крупномасштабных съемок пункты теодолитных ходов выбирают на участках с хорошим обзором. При съемке застроенной территории линии ходов должны проходить вдоль фасадной линии застройки.

Р исунок 65 теодолитные ходы

Вершины ходов закрепляют на местности кольями или металлическими штырями. Средняя длина сторон хода может быть 100 – 200 м, минимальная – 20 м. Предельная длина ходов может быть до 600 м (для съемки масштаба 1:500) и 1500 м (в масштабе 1:1000). Длины линий в теодолитных ходах измеряются мерной рулеткой или точным дальномером с относительной погрешностью не хуже , а углы измеряются теодолитом одним полным приемом с точностью 0,5 – 1,0'.

После выполнения полевых измерений приступают к их математической обработке, которая преследует три цели:

1) устранение геометрических несогласий в построенных фигурах;

2) оценку точности выполнения измерений;

3) вычисление координат пунктов теодолитного хода.

Исходными данными при прокладке теодолитного хода обычно служат как минимум два опорных пункта с известными координатами. В математическую обработку включаются все измеренные углы поворота и горизонтальные проекции длин линий. Дирекционные углы исходных сторон или берут из каталога координат исходных пунктов или находят из решения обратных геодезических задач.

Математическую обработку начинают с определения геометрического несогласия в углах. В замкнутом ходе сумма внутренних углов должна быть равна 180º (n–2), а отличие суммы измеренных углов от этой величины составит угловую невязку

. (97)

В разомкнутом ходе, проложенном между начальной и конечной сторонами с заданными дирекционными углами, угловые невязки получают по формулам:

(98)

для левых по ходу углов поворота;

(99)

для правых углов поворота.

Невязки в углах не должны превышать величины

, (100)

где t – точность измерения углов теодолитом.

Если невязка не выходит за пределы допуска, то ее распределяют между измеренными углами поровну, так что каждый угол получает поправку

. (101)

Сумма исправленных углов должна приводить к нулевой угловой невязке. После устранения угловой невязки последовательно вычисляют дирекционные углы всех сторон хода, используя исправленные углы поворота β:

(102)

при левых углах поворота;

(103)

для правых углов поворота.

При расчете по этим формулам следует иметь в виду, что дирекционные углы – положительные числа и находятся в пределах от 0˚ до 360˚.

Следующим этапом таких приближенных уравнительных вычислений будет вычисление приращений координат по всем сторонам хода

(104)

В замкнутом ходе суммы приращений координат теоретически должны быть равны нулю, и потому невязки в координатах

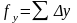и . (105)

В разомкнутом ходе, проложенном между двумя опорными пунктами

Полная линейная невязка определяется по теореме Пифагора

. (106)

Ее считают допустимой при условии

. (107)

Если это условие выполнено, то невязки в координатах распределяют между приращениями координат с обратным знаком пропорционально длинам сторон хода, то есть каждое приращение получает поправку

; . (108)

Если невязки составляют несколько сантиметров, то их можно распределить на глаз.

В заключение по исправленным приращениям координат последовательно вычисляют координаты всех точек хода, опираясь на исходные пункты.