14.3. Определение допустимых температурных перепадов

В соответствии с 14.2 при решении задачи предотвращения трещинообразования в блоке прежде всего следует определить допустимые перепады температур для конкретных условий и технологию, которая бы обеспечила выполнение этого условия.

Обычно задачу решают таким образом. Для заданных конкретных ус­ловий бетонирования блока (состав бетона, температура бетонной смеси, условия тепловыделения и теплоотдачи из блока и т.д.) рассчитывают изменение температурного поля в блоке во времени. Далее по детальным формулам семейства (14.1) определяют температурные напряжения. При этом продолжительность времени, за которое определяют температурные напряжения, делят на ряд интервалов и для каждого интервала опреде­ляют приращения напряжений с учетом конкретного измерения температуры бетона, модуля упругости во времени и всех других характерис­тик бетона и коэффициентов, входящих в формулы.

Для блоков, расположенных на "жестком основании", приращение вынужденных напряжений составит:

а) при полном "защемлении": ;

б) при "неполном защемлении": .

Задаваясь различными мероприятиями по регулированию температур­ного режима в блоке и, как следствие, изменяя температурное поле и при­ращение, определяют суммарные напряжения при различных наборах меро­приятий и выбирают тот вариант, при котором суммарные напряжения не превосходят допустимых:

.

Указанные подробные расчеты термонапряженного состояния блоков достаточно трудоемки и их выполняют обычно с помощью программ на ЭВМ. То же касается расчетов температурных полей в блоках бетонирования. Однако практика проектирования выработала и более простые, приближенные методы решения практических задач, возникающих при определении требований к температурному режиму блоков и назначении различных ме­роприятий по их обеспечению, которые дают приемлемые для предварительных прогнозов результаты. Один из этих методов изложен ниже.

Основным допущением в этом методе является принятие осредненных значений величин , , , для всего интервала времени. Тогда

.

Приняв , получим: .

В предельном случае: ,

откуда допустимый температурный перепад средних температур в блоке

, (14.6)

а допустимый перепад максимальных температур в блоке

, (14.7)

где – переходный коэффициент от средней температуры в блоке в период экзотермии к максимальной. Этот коэффициент зависит от условий теплообмена блока с окружающей средой и определяется по результатам расчета температурного поля в блоке или для предварительных расчетов – по аналогам.

14.4. Факторы, влияющие на величину допустимого перепада температур

Для того чтобы выявить эти факторы, рассмотрим последовательно все члены, входящие в формулы (14.2) – (14.6).

Предельная растяжимость бетона определяется лабораторными исследованиями при подборе состава бетона. При быстром приложении внешней силы предельная растяжимость бетона меняется в пределах от до в зависимости от состава и марки бе­тона.

Нормативными документами рекомендованы следующие средние значения предельной растяжимости бетона:

Марка бетона

Предельная растяжимость

В то же время опытами установлено, что предельная растяжимость несколько увеличивается, если нагрузка возрастает медленно, как это обычно имеет место при температурных воздействиях. Как и прочность бетона и модуль упругости бетона, предельная растяжимость изменяется с возрастом бетона. Рост предельной растяжимости , происходит несколько медленнее, чем рост модуля упругости , и быстрее, чем рост прочности (рис. 14.4).

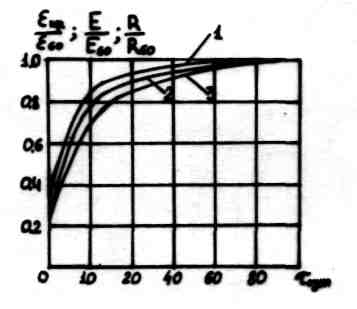
Рис. 14.4. Зависимость механических характеристик бетона от возраста

I – изменение модуля упругости;

2 – изменение предельной растяжимости; 3 – изменение прочности бетона

Опытами установлена также зависимость предельной растяжимости бетона от градиента напряжений в нем. Это особенно важно учитывать при расчете термонапряженного состояния блоков, так как температурные напряжения часто характеризуются высокими градиентами. При наличии значительного градиента температурных напряжений предельная растяжимость бетона при расчете его трещиностойкости может быть принята в 1,5 – 2 раза больше, чем соответствующая величина, определенная при одноос­ном растяжении.

Из других факторов, влияющих на фактическую предельную растяжимость в блоке, существенное влияние оказывают состав бетона и его однородность. Чем выше однородность бетонной смеси, тем при прочих равных условиях выше предельная растяжимость. Однородность бетонной смеси можно повысить целым рядом технологических мероприятий: применением большего количества фракций как крупного, так и мелкого заполнителя, обеспечением тщательного перемешивания бетонной смеси, обеспечением условий нерасслаиваемости бетонной смеси при транспортировании и укладке и др.

Таким образом, εпр = φ(M, , состава, однородности, возраста бетонной смеси), (14.8)

Коэффициент линейного расширения изменяется в зависимости от состава бетона и колеблется в пределах . При вы­держивании высокой однородности состава бетона и положительной темпе­ратуры коэффициент линейного расширения относительно стабилен. Одна­ко он существенно возрастает после замерзания бетона. Так, при температуре (– 5… – 20)°С значение коэффициента линейного расширения увеличивается на 40 – 50%, а при дальнейшем понижении температуры снижается. При этом он все же на 20% выше, чем для талого бетона. В целом =φ (состава бетонной смеси, однородности, и температуры бетона). (14.9)

Коэффициент релаксации Кр является следствием ползучести бетона. Под коэффициентом релаксации Кр понимают степень изменения на­пряжения за время , считая от момента приложения нагруз­ки при условии, что относительная деформация за это время остается постоянной. Это явление характеризуется кривой релаксации напряжений изображенной на рис. 14.5, причем изменение различно для бетона разных возрастов. Таким образом, функционально коэффициент релаксации

, (14.10)

где: – возраст бетона в момент начала охлаждения бетонной кладки; – возраст бетона к моменту остывания бетонной кладки до средней эксплуатационной температуры (до температуры омоноличивания); – продолжительность остывания блока.

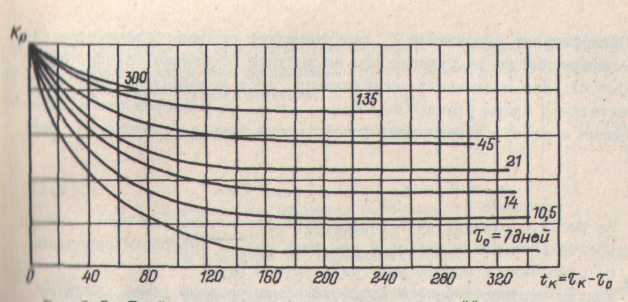
Рис.14.5. График для определения значений коэффициентов релак­сации (затухания) температурных напряжений – возраст бетона к началу интенсивного охлажде­ния бетонной кладки; – возраст бетона к момен­ту охлаждения бетонной кладки до температуры омоноличивания строительных швов; – продолжитель­ность охлаждения.

Коэффициент защемления Кз характеризует степень ограничения свободы деформаций из-за укладки его на жесткое основание (скалу, старый бетон). Как показывают исследования, этот коэффициент зависит от относительной длины блока , т.е. от размеров блока бетонирования и от отношения модулей деформации бетона и основания (рис. 14.6)

Кз=φ , (14.11)

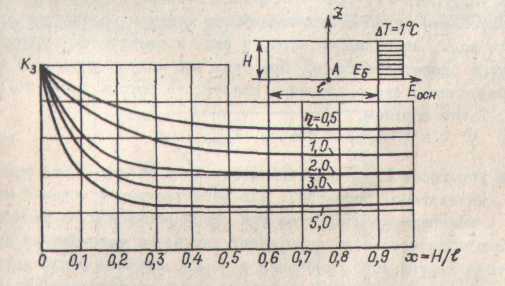
Рис. 14.6. График для определения коэффициента защемления в нижней точке А

прискального блока при равномерном остывании – нагреве:

Из рис. 14.6 следует, что коэффициент защемления тем выше, чем выше относительная длина блоков и чем выше модуль упругости основания Eосн по отношению к модулю упругости бетона Eбет.

Модуль упругости бетона Ебет, как было сказано ранее, зависит от возраста бетона. В возрасте 7-10 сут. модуль упруго­сти составляет 0,6 - 0,7 от годичного а в возрасте 3-4 сут. он еще меньше. В зрелом возрасте модуль упругости гидротехнического бетона составляет 200 000 – 400 000 кг/см². Средние значения его зависят от марки бетона:

Марка бетона MI00 М200 М250 М300 М400

Модуль упругости 1,7·105 2,4·105 2.65·I05 2,9·105 3,3·I05

При замерзании бетон становится более жестким вследствие превращения части воды, заполняющей поры, в лед, и ожесточения структурных связей внутри цементного камня. При этом его модуль упругости возрас­тает по сравнению с его значениями для талого бетона примерно в полтора раза. Таким образом,

Eбет = φ (М, возраст бетона, Tбет). (14.12)

Модуль упругости Eосн существенно зависит от категории основания (скальное, нескальное, бетонное). Для естественных оснований модуль упругости к моменту строительства уже сформировался и не зависит о времени. Это обстоятельство определяет изменение соотношения характеристик бетона и скального основания в первые моменты после укладки бетона. Если вначале скальное основание может рассматриваться как достаточно жесткое относительно бетона, то в возрасте месяца и более картина меняется и жесткость бетона становится равной жесткости основания или больше ее. В зависимости от трещиноватости скальных оснований модуль их деформации изменяется в пределах З·104 – З·105кг/см², а средние значения колеблются для малотрещиноватой скалы в пределах (180-300)·103 кг/см², для скалы средней трещиноватости в пределах (100-180)·103 кг/см², а для сильнотрещиноватой скалы – (30-100)·103 кг/см². Модуль деформации нескальных грунтов изменяется в пределах (0,6-6,0)·103 кг/см². Таким образом,

Eосн = φ (категорий пород, их трещиноватости). (14.13)