Оглавление

1. Трендовые модели прогноза 3

2. Расчетное задание 5

Список используемой литературы 7

1. Трендовые модели прогноза

К наиболее распространенным методам прогнозирования относится экстраполяция. Экстраполяция – это метод, при котором прогнозируемые показатели рассчитываются как продолжение динамического ряда на будущее по выявленной закономерности развития. По сути экстраполяция является переносом закономерностей и тенденций прошлого на будущее на основе взаимосвязей показателей одного ряда. Метод позволяет найти уровень ряда за его пределами, в будущем. Экстраполяция эффективна для краткосрочных прогнозов, если данные динамического ряда выражены ярко и устойчиво.

Если фактическое развитие увязывается с гипотезами о динамике процесса развития с учетом физической и логической сущности, то говорят о прогнозной экстраполяции. Прогнозная экстраполяция может быть в виде тренда, огибающих кривых, корреляционных и регрессионных зависимостей, может быть основана на факторном анализе и др. Экстраполяция сложного порядка может перерасти в моделирование.

Для такого вида экстраполяции, как тренд, характерно нахождение плавной линии, отражающей закономерности развития во времени. Тренд обычно применяется как основная составляющая прогнозируемого временного ряда, на которую накладываются другие составляющие, например сезонные колебания.

Экстраполяция на основе тренда включает:

- сбор информации эмпирического ряда показателя за прошлые периоды;

- выбор оптимального вида функции, описывающей указанный ряд с учетом его сглаживания и выравнивания;

- расчет параметров выбранной экстраполяционной функции;

- расчет прогноза на будущее по выбранной функции.

В настоящее время насчитывается большое количество типов кривых роста для экономических процессов. Чтобы правильно подобрать наилучшую кривую роста для моделирования и прогнозирования экономического явления, необходимо знать особенности каждого вида кривых.

Наиболее часто в экономике используются:

1. линейные тренды;

2. экспоненциальные тренды;

3. логарифмические тренды;

4. степенные тренды;

5. полиномиальные тренды;

6. S-образные кривые роста.

Выбор той или иной функции для выравнивания ряда динамики осуществляется, как правило, на основании графического изображения эмпирических данных, дополняемого содержательным анализом особенностей развития исследуемого показателя (явления) и специфики разных функций, их возможности отразить те или иные нюансы развития. Определенную вспомогательную роль при выборе аналитической функции играют также механические приемы сглаживания (укрупнение интервалов и метод скользящей средней). Частично устраняя случайные колебания, они помогают более точно определить тренд и выбрать адекватную модель (уравнение) для аналитического выравнивания.

Выравнивание по прямой (или линейной функции) используется, как правило, в тех случаях, когда абсолютные приросты практически постоянны, т.е. когда уровни изменяются в арифметической прогрессии (или близко к ней).

Выравнивание по показательной функции используется в тех случаях, когда ряд отображает развитие в геометрической прогрессии, т.е. когда цепные коэффициенты роста практически постоянны.¹

Полиномиальные кривые роста имеют вид полинома k-й степени: . Полиномиальные кривые роста можно использовать для аппроксимации (приближения) и прогнозирования экономических процессов, в которых последующее развитие не зависит от достигнутого уровня.

Экспоненциальные кривые роста предполагают, что дальнейшее развитие зависит от достигнутого уровня, например, прирост зависит от значения функции. В экономике чаще всего применяются две разновидности экспоненциальных (показательных) кривых:

- простая экспонента, которая представляется в виде функции , где а и b — положительные числа, при этом если b > 1, то функция возрастает с ростом времени t, если b < 1 — функция убывает.

- модифицированная экспонента имеет вид , где постоянные величины: а < 0, b положительна и меньше единицы, а константа k носит название асимптоты этой функции, т.е. значения функции неограниченно приближаются (снизу) к величине k.

Для моделирования процессов, которые сначала растут медленно, затем ускоряются, а затем снова замедляют свой рост, стремясь к какому-либо пределу, используются так называемые S-образные кривые роста, среди которых выделяют кривую Гомперца и логистическую кривую.

Кривая Гомперца имеет аналитическое выражение , где а, b — положительные параметры, причем b меньше единицы; параметр k — асимптота функции.

В кривой Гомперца выделяются четыре участка: на первом — прирост функции незначителен, на втором — прирост увеличивается, на третьем участке прирост примерно постоянен, на четвертом — происходит замедление темпов прироста и функция неограниченно приближается к значению к. В результате конфигурация кривой напоминает латинскую букву S.

Логистическая кривая, или кривая Перла-Рида — возрастающая функция, наиболее часто выражаемая в виде . другие виды этой кривой: ; .

В этих выражениях а и b — положительные параметры; k — предельное значение функции при бесконечном возрастании времени.

Конфигурация графика логистической кривой близка графику кривой Гомперца, но в отличие от последней логистическая кривая имеет точку симметрии, совпадающую с точкой перегиба.

Универсальным методом предварительного выбора кривых роста, позволяющим выбрать кривую из широкого класса кривых роста, является метод характеристик прироста. Он основан на использовании отдельных характерных свойств кривых, рассмотренных выше. При этом методе исходный временной ряд предварительно сглаживается методом простой скользящей средней: .

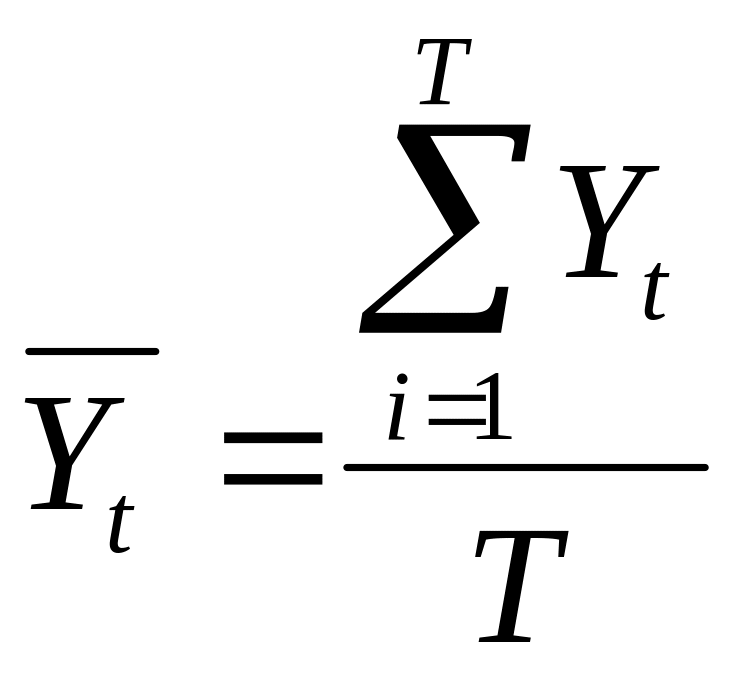Затем вычисляются первые и вторые средние приросты: , , t=2,3,…,n-1.

А также ряд производных величин, связанных с вычисленными средними приростами и сглаженными уровнями ряда: ; ; ; .

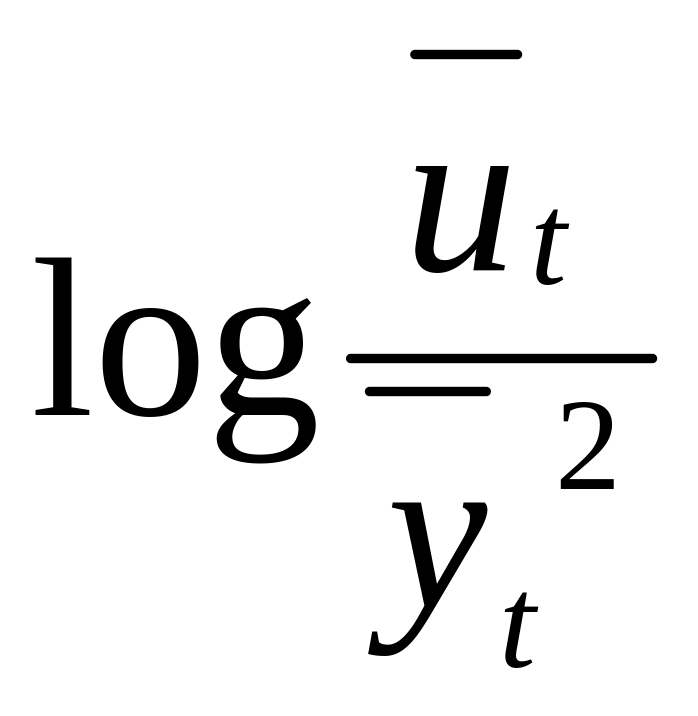В соответствии с характером изменения средних приростов и производных показателей выбирается вид кривой роста для исходного временного ряда, при этом используется специальная таблица.

Наиболее распространенный метод нахождения параметров тренда – метод наименьших квадратов (МНК). При этом методе учитываются все эмпирические уровни и должна обеспечиваться минимальная сумма квадратов отклонений эмпирических значений уровней y от теоретических ŷ_t , т.е. ∑ (y – ŷ_t )² = min.

В частности, при выравнивании по прямой вида ŷ_t = a₀ + a₁t параметры a₀ и a₁ определяются путем решения системы нормальных уравнений, полученной методом наименьших квадратов (заменой x на t),

где n – количество уровней ряда;

t – порядковый номер в условном обозначении периода или момента времени

y – уровни эмпирического ряда.

Как уже отмечалось, выравнивание по показательной функции проводится, в основном, когда уровни ряда меняются в геометрической прогрессии, т.е. цепные коэффициенты роста более или менее постоянны.

Нетрудно заметить, что логарифм показательной функции представляет собой линейную функцию . Поэтому, если заменить уровни ряда их логарифмами, параметры a₀ и a₁ можно определить (через их логарифмы), решая следующую систему нормальных уравнений, полученную методом наименьших квадратов:

или при счете от середины ряда ( когда ∑t = 0)

Откуда получаем:

;

Парабола 2–го порядка ŷ_t = a₀ + a₁t + a₂t² как уравнение тренда может быть использована для выравнивания таких рядов, уровни которых сначала возрастают, а затем снижаются (или наоборот), или в рядах, где вторые разности уровней примерно постоянны. Обычно при этом ориентируются по графическому изображению эмпирических данных.

Минимальное количество данных для построения трендовой модели должно не менее, чем в 3 раза превышать количество параметров модели, таким образом, для построения параболы второго порядка необходимо как минимум 9 наблюдений.

Параметры искомого уравнения тренда a₀, a₁ и a₂ определяют, решая систему нормальных уравнений, полученных методом наименьших квадратов:

или при счете от середины ряда ( когда ∑t = 0)

тенденции (тренда) изменения уровней за исследуемый период.