Вопрос 26.

Равновесие между водой и гидрофобными жидкостями. Коэффициенты растворимости и распределения органических компонентов и методы их определения

Массообмен с гидрофобными веществами

Гидрофобными веществами (hydrophobic matter) в данном случае считаются любые преимущественно жидкие скопления неполярных практически нерастворимых в воде, в основном органических соединений. В из составе преобладают углерод (80-90% веса) и водород (10-15%). Заметную роль играют кислород, сера и азот. Они могут быть подвижными жидкими (нефти, нефтепродукты) , неподвижными вязкими (мальты, асфальты и пр.) и даже твердыми (торф, уголь, гумус почв и т.д.). Все рассматриваемые гидрофобные вещества, прежде всего, удобно разделить на неподвижные и подвижные.

Неподвижные гидрофобные вещества представлены преимущественно сложными органическими образованиями, остатками планктона и растительности. У поверхности наиболее концентрированной формой такого органического вещества являются торф и гумус почвенного слоя. На больших глубинах имеет место преимущественно рассеянное органическое вещество, весовая доля которого обычно не превышает 1-2%. Относительное содержание этого органического вещества в породах характеризуется средним весовым содержание его углерода , которое в глинистых породах равно приблизительно 1%, в песчано-алевритовых и мергелях - 0,4%, в карбонатах – 0,2%. К неподвижными с некоторой долей условности можно отнести и тяжелые твердые битумы, асфальты и озокериты. Таким образом, неподвижное гидрофобное вещество по существу представляет собой органическое вещество породы или осадков.

Подвижные гидрофобные жидкости это сложные растворы, в составе которых преобладают органические вещества, алкановые, нафтеновые и ароматические углеводороды с высоким молекулярным весом. Большинство их компонентов в чистом виде и в стандартном состоянии находится в жидком и парообразном состояниях. Эти жидкости выделяет их миграционная подвижность, которая в значительной степени зависит от их плотности и вязкости. Они, как и подземные газы, способны мигрировать относительно подземной воды, и аккумулироваться в виде скоплений, в частности залежей нефти. Присутствие гидрофобных жидкостей на малых глубинах связано, как правило, с загрязнением геологической среды нефтепродуктами (бензин, керосин, дизельное топливо, толуол и т.д.).

Параметры равновесия

Взаимодействие гидрофобной жидкости с породой, водой и подземным газом в условиях относительно низких температур связано с физической сорбцией. Часть её поглощается породой в количесве так называемой минимальной или остаточной насыщенности (residual saturation). Вторая часть испаряется (улетучивается) в подземный газ, и третья часть растворяется в воде. Все эти процессы и составляют массообмен гидрофобной жидкости с окружающей геологической средой.

При достижении абсорбционного равновесия любой компонент i распределяется так, что его парциальные давления во взаимодействующих средах равны одной и той же величине p_i. Поэтому для оценки равновесного распределения компонента i в сравниваемых средах достаточно сопоставить его парциальные давления в них. Поэтому отношение служит показателем степени насыщения воды компонетом i относительно гидрофобной жидкости, а величина - индексом их неравновесности. При равновесии степень насыщения равна 1, а индекс – нулю. Если степень насыщения больше 1 (индекс <0), вода перенасыщена относительно гидрофобной жидкости, если меньше (индекс > 0), вода недонасыщена.

Чаще показателем равновесности воды и гидрофобной жидкости по компоненту i чаще используют коэффициент распределения в уравнениях (II-351). Если , то компонент i мигрирует из воды в гидрофобную жидкость, а если , то наоборот. При достижении равновесия .

В связи с этим для оценки поведения неполярных компонентов на границе воды и гидрофобная жидкость необходимо сравнить либо их парциальные давления, либо концентрации в мольных долях.

При полном равновесии суммы парциальных давлений компонентов в воде и в гидрофобной жидкости равны:

, (II‑1)

где - даление насыщения гидрофобной жидкости. Парциальное давление любого неполярного компонента в воде, как и газового, можно определить с помощью коэффициентов растворимости Генри или Бунзена, определенных при парциальном давлении 1 атм, по уравнениям (II-352) и (II-379), соответственно. Как правило, используют коэффициент Генри.

Необходимо помнить, что у компонентов с давлением насыщенного пара меньше 1 атм величины коэффициентов растворимости не соответствуют самой растворимости в стандартных условиях. При стандартных условиях эти компоненты растворяются в воде при парциональном давлении равном давлению насыщенного пара P_i⁰, что заметно ниже 1 атм. Поэтому коэффициент растворимости Генри для таких компонентов равен связан с растворимостью уравнением:

, (II‑2)

где - величина растворимости компонента i при его парциальном давлении равном P_i⁰. Коэффициент растворимости Генри, как и в случае газовых компонентов, выражают в атм·л·мл^-1, в атм·л·моль^-1, но чаще всего в атм·м³·моль^-1. Если величина давления насыщенного пара выражена в мм ртутного столба, а растворимость в весовых единицах, то

, (II‑3)

где - давление насыщенного пара в мм рт.ст., M_i - молекулярный вес гидрофобного компонента, а C_в,max,i – растворимость того же компонента в мг·л^-1. Достаточно часто коэффициент Генри выражают безразмерной величиной, как соотношение концентраций, выраженных в одинаковых единицах (коэффициент растворимости Оствальда):

, (II‑4)

где – безразмерный коэффициент растворимости Генри, а P =1 атм.

Как водно из уравнений (II-392 и II-393), коэффициент растворимости Генри (H_M,i) пропорционален величине давления насыщенного пара и может служить мерой летучести неполярных компонентов. Поэтому Дональд Маккей и Янг Шу (Mackay, D., Shiu W.Y., 1981) предлогают использовать его для классификации компонентов по летучести:

• Высоко летучие, если H_i > 10^-3 атм·м³·моль^-1 (испарение быстрое),

• Летучие, если H_i находится в интервале 10^-3 to 10^-5 атм·м³·моль^-1 (испарение значительное),

• Полулетучие, если H_i находится в интервале 10^-5- 3×10^-7 атм·м³·моль^-1 (испарение медленное),

• Нелетучие, если H_i <3×10^-7 атм·м³·моль^-1 (испарение не значительное).

При низких концентрациях равновесные парциальные давления органических соединений в воде, гидрофобной жидкости и подземном газе равны, и согласно уравнениям II-352, II-374 и II-384, соблюдают равенство:

. (II‑5)

Для определения парциального давления любого органического соединения i необходимы сведения по величинам его растворимости или коэффициентов растворимости о в подземной воде и гидрофобном веществе. Эти величины для пресной воды можно найти в справочной литературе. Давления насыщенного пара и параметры растворимости для наиболее актуальных компонентов приведены в таблице II-39. Как правило, давление насыщенного пара дается в мм рт. ст., реже в Па или атм. 1 мм рт. ст. равен 133,3224 Па или 1,31610^-3 атм.

Однако, во-первых, природные воды представляют собой растворы электролитов, что необходимо учитывать,согласно уравнению II-364. Растворимость неполярных соединений с ростом минерализации падает. Так например, коэффициент Сеченова в нормальных условиях равен для фенола 0,133, для бензола и нитробензола 0,166, для анилина 0,130 (Сергеева В.Ф., 1965). Во-вторых, природные гидрофобные вещества представляют собой сложные растворы, для которых параметры раствормости отдельных компонентов, как правило, отсутствуют. В связи с этим определение парциального давления в природных органических растворах представляет собой слишком сложную задачу, решение которой связано с использованием уравнений состояния. Поэтому при оценке равновесности подземных вод и гидрофобных растворов органических веществ препочитают пользоваться коэффициентами распределения.

Рисунок II-1. Молекулярная масса, давление насыщенного пара, растворимость и коэффициент углеродного распределения некоторых органических компонентов.

Соединения	Формула	Mi	Давление насыщенного пара в мм Hg при 20°C.	Коэффициент растворимости Генри, атм·м3моль-1 (оС)	Растворимость при 1 атм, Моль/л при 20°C.
ГАЛОГЕНИЗИРОВАННЫЕ УГЛЕВОДОРОДЫ
Метил хлорид (Хлорометан)	CH3Cl	50,48	5 атм (г)	5,84·10-3 (17,5) оС	0,005556 0,0077-0,0071
Метилендихлорид (Дихлорметан)	CH2Cl2	84,93	349	3·10-3 1,31·10-3 17,5 оС	0,0065 0,00426
Хлороформ (Трихлорметан)	СНСl3	119,38	160	4,8 ·10-3 2,46·10-3 17,5 оС	4,39·10-2 6,7·10-2 6,87·10-2
Тетрахлорметан	CCl4		90	2,3 ·10-2 2,11·10-2 17,5 оС	5,15·10-3
Четыреххлористый углерод	CCl4	153,82	91	21,1·10-3 17,5 оС	5,2·10-3 5,1·10-3
Бромоформ	СНВr3	252,75	5,6 (25°С)	5,8 ·10-4 с	1,27·10-2 1,19·10-2-1,26·10-2
Метилбромид	CH3Br	94,94	1420 (г)		9,48·10-3
1,1-Дихлорэтан	CHCl2CH3	98,97	180	4,3 ·10-3 с 3,89·10-3 17,5 оС	5,51·10-2 5,56·10-2 5,56·10-2
1,2-Дихлорэтан	CH2ClCH2Cl	98,97	61	9,1·10-4 с	8,82·10-2 8,78·10-2 8,78·10-2
1,1 -Дихлорэтен	H2C=CCl	61,49	500	—	6,50·10-3
Хлорэтан (этилхлорид)	CH2ClCH3	64,51	1000 (г)	8,46 ·10-3 17,5 оС	8,90·10-2
Транс-1,2-дихлорэтен	CHCl=CHCl	96,94	200 (14°C)	4,2 ·10-2 с 6,6·10-3 17,5 оС	6,37·10-3 6,19·10-3 6,19·10-3
1,1,1-Трихлорэтан	ССl3СН3	131,39	100	18 ·10-3 12·10-3 17,5 оС	7,31·10-3 33,49·10-3 3.65·10-3-33,49·10-3
Трихлорэтилен (TCE)	Cl2C=CHCl	131,39	60	10 ·10-3 6,32·10-3 17,5 оС	7,89·10-3 8,37·10-3 25 оС 8,37·10-3
1,1,2-Трихлорэтан	CH2ClCHCl2	133,40	19	7,4 ·10-4 с	3,38·10-2 3,37·10-2 3,37·10-2
1,1,2,2-Тетрахлорэтан	CHCl2CHCl2	167,86	5		17,28·10-3 17,28·10-3
1,2,2,2-Тетрахлорэтан	CCl3CHCl2
Тетрахлорэтилен	CCl2=CCl2	165,82			0,90·10-3-1.21·10-3
Пентахлорэтан	CCl3CCl3	236,74	3,4		0,21·10-3 22 оС
Гексахлорэтан	ССl3СН3
Тетрахлорэтилен (Перхлорэтилен)	С12С=СС12	165,82	14	8,3 ·10-3 11,7·10-3 17,5 оС	2,22·10-3 0,90·10-3 25 оС
Винил хлорид (Хлорэтен)	С H2=СHС1	62,49	2660 25 оС (г)	19,3·10-3 17,5 оС	1,76·10-5 25 оС 1,76·10-5-0,96·10-3
1,1-Дихлорэтен (Винилиденхлорид)	СС12=СH2	96,94	500	19,1·10-3 17,5 оС
Цис-1,2-Дихлорэтен	CHCl=CHCl	96,94	200 25 оС	2,65·10-3 17,5 оС	8,25·10-3
1,2-Дихлорпропан					2700мг/л
1,3-Дихлорпропилен					2700-2800 мг/л
Этилбензол	C6H5CH2CH3	106,17			1,43·10-3
Хлорбензол	C6H5Cl	112,56	8,7		3,98·10-3
АРОМАТИЧЕСКИЕ УГЛЕВОДОРОДЫ
Бензол	C6H6	78,12	76 74,8	5,5 ·10-3	1,82·10-2 1,05·10-2-2,3·10-2
Фенол	C6H5OH	94,12	0,2	3,0 ·10-7 с	8,77·10-1
Хлорбензол	C6H5C1	112,56	8,8	2,6 ·10-3 с	4,45·10-3 3,98·10-3-4,44·10-3
Этилбензол	C6H5C2H5	106,17	7	8,7 ·10-3	1,06·10-3
Толуол	С6Н5СН3	92,14	22	5,7 ·10-3	5,08·10-3 5,80·10-3
o-Ксилол	С6Н4(СН3)2	106,17	5	5,3 ·10-3	1,24·10-3
ДРУГИЕ ОРГАНИЧЕСКИЕ РАСТВОРИТЕЛИ
Ацетон	СН3-СО-СН3	58,08	89(5°C)	—
Диэтиловый эфир	С2Н5OС2Н5		442	5,1·10-4 с	1,14
Тетрагидрофуран	С4Н8O	72,10		—
1,4-Диоксан	O(CH2-CH2)2O		30	—
1-Октанол	CH3(CH2)6CH2OH	130,23
BIOCIDES
Пентохлорфенол	СбСl5ОН		1.1·10-4	3,4·10-6	4,26·10-5
DDT	(СlС6Н4)2СНССl3		1·10-7	3,8·10-5	3,46·10-9
Линдан (гексахлорциклогексан)	СбН6Cl6	290,86	9,4·10-6	4,8·10-7	2,58·10-5

²атм-м³/моль;

с -показывает величины, рассчитанные по данным давления пара и растворимости.

Скорректированные из( Jackson R.E. et al., 1985, ).

Коэффициенты распределения любого компонента между подземной водой и гидрофобной жидкостью в условиях равновесия обычно характеризуют соотношением концентраций в мольных долях (см. уравнение II-351). Если в условиях низких давлений, например, в зоне аэрации, приравнять парциальные давления компонента i в подземном газе и гидрофобной жидкости и воде, то получим:

. (II‑6)

Это уравнение позволяет связать равновесные концентрации компонента i в сравниваемых средах. Действительно, согласно равенствам (II-351) и (II-389) уравновешенные коэффициенты распределения компонента i в этих трех средах связаны уравнением:

, (II‑7)

где - коэффициент распределения компонента i между гидрофобной жидкостью и подземным газом. В стандартных условиях (при P =1 атм) этот коэффициент распределения численно равен величине давления насыщенного пара.

Так как органические вещества, с которыми взаимодействуют подземные воды, как правило, представляют собой сложные смешанные растворы неизвестного состава, в практике геохимических и экологических исследований вместо коэффициента распределения для чистого органического растворителя используют коэффициент распределения , определенный для конкретного природного органического вещества. Этот коэффициент распределения абсорбции органическим веществом представляет собой отношение весовых уравновешенных концентраций отдельного неполярного компонента i в органическом веществе и, согласно уравнениям I-18 и II-388, равен:

. (II‑8)

Здесь 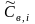- весовая концентрация компонента i в органическом веществе, ν_ср – средний молекулярный объем органического вещества, см³·моль^-1, γ_w – удельный вес воды, г·мл^-1, m - минерализация воды, мг·л^-1, 18,016 г моль^-1- молекулярная масса H₂O.

Однако, достаточно часто содержание органического вещества часто выражено через содержание его органического углерода . В таком случае необходимо иметь представление о равновесной концентрации компонента i отнесено веса не всего органического вещества, а только его углерода. Согласно опытным данным вес органического вещества пород приблизительно в 1,724 раза превосходит вес углерода в нём. Отсюда и концентрация любого абсорбированного компонента i по отношению к весу органического углерода должна быть приблизительно в 1,724 раз больше величины . Поэтому можно считать, что коэффициент распределения абсорбции органическим углеродом равен:

. (II‑9)

Величины и , очевидно, зависят от состава воды и природы органического вещества. Можно полагать, что их величины ростут с минерализацией, согласно уравнению II-364. Но коэффициенты Свыченко для природных органических веществ отсутствуют. Замечено, что абсорбции так же препятствует увеличение pH . Исследования показывают, что величина коэффициента растет и вследствие увеличением зрелости органического вещества. Поэтому, например, величина бензола в разных условиях может меняться от 32 до 97. Однако, влияние этих факторов пока исследовано недостаточно, и наиболее достоверными являются величины , полученные непосредственно экспериментально для каждого конкретного случая.

При отсутствии экспериментальных данных для определения величин коэффициентов распределения и широко используется метод аналогий. Для этого в качестве стандартного аналога, как правило, используют октанол, т.е. октиловый спирт (CH₃(CH₂)₆CH₂OH), который является хорошим органическим растворителем, но плохо растворим в воде. Коэффициент равновесного распределения любого компонента i между чистой водой и октанолом будем называть коэффициентом распределения абсорбции октанолом (Octanol-water partition coefficient). Его величина определяется, как отношение равновесных весовых концентраций одного неполярного компонента i в октаноле и в воде:

. (II‑10)

Здесь 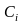и – концентрация компонента i в октаноле и в воде соответственно. Величина этого коэффициента безразмерная. В случае ионизируемых органических соединений, предворительно устанавливается такое pH раствора, при котором они нейтральны. Этот коэффициент первоначально использовали как показатель возможного накопления токсичных компонентов в жировых тканях организмов. Октанол играет роль липидов (жиров), а вода – окружающей среды. Благодаря этому величины коэффициента распределения абсорбции октанолом определены почти для всех опасных органических соединений и их можно легко найти в справочной литературе.

Исследования показали, что величины растворимости органических соединений в воде C_M,max,i, а также коэффициенты , и в наибольшей степени зависят от их природы и в меньшей степени от растворителя. Поэтому все эти параметры связаны между собой функциональными зависимостями, которые позволяет использовать один параметр для оценки другого.

Как правило, чем выше растворимость компонента i в воде, тем ниже его растворимость в органическом веществе. Поэтому величины и находятся в обратной зависимости от величин растворимости компонентов в воде C_M,max,i. Это позволяет при отсутствии экспериментальных данных оценивать величину либо по величинам коэффициента растворимости в воде, либо по октанол-водномоу коэффициенту распределения) , либо даже по самой структуре молекулы абсорбата.

Существует много эмпирических уравнений, описывающих обратную зависимость от величины растворимости C_в,max,i. Последним и наиболее общим среди них является уравнение, предложенное Дж. Хассеттом и др. в 1983 году (Hassett J.J., и др., 1983):

, (II‑11)

где растворимость C_в,max,i измеряется в мгл^-1.

Однако величины растворимости органических веществ в природной воде, в свою очередь, зависят от условий эксперимента (температуры, чистоты вещества и ион­ной сила раствора). Так как эти параметры не всегда публикуются, использование чужих значений растворимости не всегда достаточно корректно.

Величины коэффициентов распределения и разных органических компонентов, как правило, связаны между собой прямой зависимостью. Предложено много эмпирических уравнений этой зависимости от для разных соединений или их групп. Гидрогеологи и инженеры, ко­торые хотят определить величину , оказываются в ситуации вы­бора, какое уравнение использовать. Наилучшим выбором является урав­нение для соединений близких к иссле­дуемому по составу и свойствам. Наиболее общим является эмпирическое уравнение Дж. Хассетта и др. (Hassett J.J. et al., 1983):

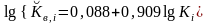, (II‑12)

где имеет размерность см³г^-1, а - безразмерная величина.

Пример II‑11.

Вследствие аварии в зону аэрации проник чистый жидкий толуол (C₆H₅CH₃). Надо определить его максимальную концентрацию в газах зоны аэрации при 20°C. Молекулярный вес толуола 92,1 г/моль, его давление насыщенного пара 0,029 атм.

Мольная доля чистого толуола =1. Поэтому согласно закону Рауля максимальное парциальное давление толуола не превысит 0,029 атм. Тогда весовая концентрация толуола в газе

= =111 мг/л

Пример II‑2.

Вследствие аварии в зону аэрации проникло большое количество трихлорэтилена (Cl₂C=CHCl), который имеет молекулярный вес M_ТХЭ =131,4 г/моль, давление насыщен­ного пара P⁰ =60 мм рт .ст. Грунт в зоне аэрации имеет пористостью n =30%, коэффициенты остаточного насыщения водой K_ТХЭ =0,33 и трихлорэтиленом K_ТХЭ= 0,17. Необходимо определить максимальное весовое количетво трихлорэтилена, которое содержится в подземном газе 1 м³ грунта.

Коэффициент насыщенности грунта газом равен =1- K_ТХЭ- K_ТХЭ=1- 0,33- 0,17 =0,50. Поэтому доля подземного газа в объеме грунта равна n∙ =0,30∙0,50=0,15.

Парциальное давление чистого трихлорэтана в подземном газе

=7999 Па

Парциальное давление позволяет определить весовое содержание трихлорэтилена

= =436,7 г/м³.

Следовательно, в подземном газе 1 м³ зоны аэрации будет содержаться 453,7∙0,15= 68 г трихлорэтилена.

С другой стороны, существуют обратная зависимость между величиной и растворимостью компонентов в воде. Эта зависимость для раз­ных классов жидких и твер­дых органических соединений показано на Рис. II-71. С.Т. Хиу и другие (Chiou C.T. et al., 1982) предложили для всех этих компонентов уравнение регрессии:

, (II‑13)

где – коэффициент растворимости компонента i в воде, мольл^-1атм^-1.

Рисунок II-2. Зависимость между растворимостью в воде и коэффициентами октанол/водного распределения для разных органических соединений: 1-спирты, 2-кетоны, 3-сложные эфиры, 4-эфиры, 5-гало­геналкилы, 6-алкины, 7-алкены, 8-ароматические, 9-алканы, 10-органофосфаты и 11-полихлорирован­ные бифенилы (ПХБ) и ДДТ. ( Chiou, C.T, et al., 1982).

Пример II‑32.

При загрязнении зоны аэрации некоторое количество трихлорэтилена (Cl₂C=CHCl) растворилось в воде остаточного насыщения. Грунт в зоне аэрации имеет пористостью n =30%, и коэффициент остаточного насыщения водой K_w =0,33. Коэффициент растворимости трихлорэтилена в воде B_ТХЭ=1100 мг∙л^-1∙атм^-1 . Надо определить максимальное весовое количетво трихлорэтилена, которое может содерать вода в 1 м³ грунта.

Количество воды в кубическом метре зоны аэрации равно 1∙0,30∙0,33=0,10 м³. Максимальное количество трихлорэтана в 1 м³ воды в нормальных условиях равно произведению его коэффициента растворимости на величину внешнего давления (1 атм), т.е. 1∙1100 =1100 г/м³. Поэтому общее количество этого компонента в 1 м³ грунта будет равно 0,10∙1100=110 г/м³.

Пример II‑4.

В зону аэрации проник нефтепродукт. Пористость грунта n=0,2, Коэффициенты остаточного насыщения равны для воды 0,5, для нефтепродукта 0,05. После этого в воздухе зоны аэрации обнаружили присутствие бензола со средней концентрацией 503 мкг/л. Необходимо определить наибольшее суммарное содержание бензола в 1 м³ зоны аэрации.

Нефтепродукт имеет средний молекулярный вес M_ср=226 г/моль и плот­ность ρ_ср=0,810 г/см³. У бензола молекулярный вес M_Б=78,12, плотность ρ_Б=0,88 г/см³, давление насыщенного пара =76 мм рт. ст., и коэффициент растворимости в воде S_Б =1,82·10^-2 моль∙л^-1∙атм^-1.

Доля объема газовой фазы в 1 м³ зоны аэрации равна 0,2∙(1-0,5-0,05)= 0,09. Следовательно, содержание бензола в газовой фазе 1 м³ грунта равно 0,09∙503=45,3 мг/м³.

Содержание бензола в воде и нефтепродуктах можно определить по его парциальному давлению, которое рассчитывается по молярной концентрации (См. пример II-19):

атм.

Тогда мольная доля бензола в составе нефтепродукта равна

=1,55·10^-3

Величина мольной доли бензола в нефтепродукте позволяет определить эффективную растворимость бензола в воде:

∙10⁶=221 мг/м³,

В воде 1 м³ грунта может содержаться до 0,2∙0,5∙221=22,1 мг/м³ бензола. Содержание бензола в питьевой воды не должно превышать 5 мг/м³.

Для определения весовой концентрации бензола в самом нефтепродукте воспользуемся величинами M_ср и ρ_ср:

∙10⁶=434 г/м³.

Это означает, что 1 м³ грунта содержит в нефтепродукте 434∙0,05∙0,2∙1000=4340 мг/м³ бензола.

Таким образом, после инфильтрации нефтепродукта в зоне аэрации остаточное загрязнение бензолом в сумме может достигать 45,3+15,5+300= 360,8 мг на каждый кубический метр грунта.

Неподвижное органическое вещество обычно рассматривается как компонент породы или осадков. В этом случае массообмен между водой и органическим веществом пород часто определяется как абсорбция непосредственно породой, по аналогии с адсорбцией минеральных компонентов. В отличие от адсорбции абсорбция более медленный процесс, так как требует время для равномерного распределения абсорбатов внутри органического вещества. Поэтому вместо коэффициента распределения адсорбции породой ( см. ионный обмен) используют аналогичный коэффициент распределения абсорбции породой - .

Неполярные органические соединения практически не сорбируются минеральной частью пород, и поэтому абсорбционный коэффициент распределения мало зависит от их минерального состава. При содержании органического вещества в породе ниже 1% существует некоторый уровень, при котором абсорбционные способности органического и минерального вещества в грунтах уравниваются. Ниже этого уровня органические компоненты сорбируются преимущественно минеральной поверхностью, выше – органическим веществом. Эту пороговую концентрацию органического вещества в породе или осадках, ОВ_кр , называют критической (critical concentration). Величина ОВ_кр зависит от дисперсности и удельной поверхности грунта, содержания глинистых минералов и свойств самого гидрофобного компонента i. Как правило, сорбция органических компонентов минеральным скелетом ничтожно мала, и ею обычно пренебрегают.

При концентрациях органического вещества более ОВ_кр наблюдается прямая зависимость между величинами и содержанием органического вещества или его углерода в породе. Если содержание органического вещества в породе выше ОВ_кр и равно , а содержание его углерода -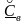 (в весовых долях), то имеем:

, ( II‑14)

где C_в,i – содержание абсорбированного компонента i в 1 грамме породы (осадка). Здесь величины измеряется в мл·г^-1 и характеризует коэффициент распределения концентраций компонента i между 1 г породы и 1 мл воды. Если компонент i в породе отсутствовал, то при взаимодействии с ней вода теряет его в количестве (см. уравнение II-272):

. ( II‑15)

Тогда, по аналогии с уравнением II-273, получим безразмерную величину коэффициента распределения:

, (II‑16)

где e – приведенная пористость, ρ – плотность скелета грунта.

Пример II‑5.

В зону аэрации с пористостью n =30% и содержанием органического углерода =0,014 попал трихлорэтилен (Cl₂C=CHCl). Растворимость трихлорэтилена в воде 1100 мг/л и коэффициент абсорбции грунта =139 мл/г. Объемная плотность осадков δ =1,85 г/см³. Необходимо определить количество трихлорэтана, поглощаемое 1 м³ осадка, т.е. q_в,ТХЭ.

Содержание трихлорэтана абсорбированного породой можно определить по уравнению:

.

Для этого необходимо рассчитать его коэффициент распределения и максимальное содержание в воде 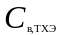. Коэффициент абсорбционного распределения равен:

=139∙0,014 =1,95 (мл/г)

Максимальное содержание трихлорэтана в воде при внешнем давлении 1 атм равно его эффективной растворимости. Так как трихлорэтан присутсвует в чистом виде и имеет C_ТХЭ=1, воспользуемся величиной его растворимости в воде 1100 мг/л. Отсюда следует, что

=1,95∙1100∙10^-6=0,002156 (г/г) или 2,16 г/кг .

Таким образом

=0,0133 г/мл или 13,300 кг/м³.