68. Структурные средние. Мода. Медиана.

Структурные средние применяются для изучения внутреннего строения и структуры рядов распределения значения признаков. К таким показателям относится мода и медиана.

Мода – [M₀] это значения средней величины встречающаяся с наибольшей вероятностью в дискретном вариационном ряду. Мода – это вариант, имеющий наибольшую частоту.

В интервальных рядах распределения с равными интервалами. Мода вычисляется по формуле:

,

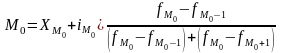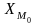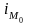где - это нижняя граница модального интервала;

- длина модального интервала;

- это частоты в модальном, предыдущем и следующим за модальным интервалом соответственно.

Модальный интервал определяется по наибольшей частоте.

Медиана – это вариант, который находится в середине вариационного ряда. Медиана делит ряд на две равные части по числу единиц со значением признака меньше медианы и со значением признака больше медианы.

Чтобы найти медиану необходимо отыскать значения признака, который находиться в середине упорядочного ряда. В ранжированных рядах, не сгруппированных данных нахождения медианы сводится к отысканию порядкового номера медианы.

Номер медианы для нечетного объема

,

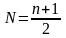где n – это число членов ряда.

В случаи четного объема ряда медиана равна средней из двух вариантов находящихся в середине ряда.

В интервальных рядах распределения медианы значения оказывается в каком – то из интервалов признака x – этот интервал характерен тем, что его накопленная сумма частот равна или превышает полусумму всех частот ряда. Значения медианы в данном случаи определяется по формуле:

,

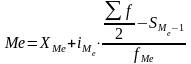где 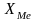- это нижняя граница модального интервала;

- длина модального интервала;

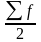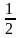- от общего числа наблюдений;

- это сумма наблюдений, накопленная до начала медианном интервала;

- это число наблюдений в медианном интервале.

68. Предельные ошибки выборки для средней и доли. Доверительные интервалы.

Cредняя ошибка выборки дает некоторое представление об ошибке репрезентативности, т. е. об ошибке, с которой выборочная средняя представляет действительное значение генеральной средней. Однако в каждой конкретной выборке ошибка может существенно отличаться от средней ошибки, т. е. нет гарантии, что ошибка, которая действительно была допущена в конкретном выборочном исследовании, не превышает средней ошибки.

Поэтому гораздо полезнее было бы знать те границы, в которых «практически наверняка» находится действительная ошибка, допущенная в данной конкретной выборке. Эти границы (пределы) указываются предельной ошибкой выборки.

По способу отбора (способу формирования) выборки единиц из генеральной совокупности распространены следующие виды выборочного наблюдения:

• простая случайная выборка (собственно-случайная);

• типическая (стратифицированная);

• серийная (гнездовая);

• механическая;

Простая случайная выборка (собственно-случайная) есть отбор единиц из генеральной совокупности путем случайного отбора, но при условии вероятности выбора любой единицы из генеральной совокупности.

Типическая (стратифицированная) выборка предполагает разделение неоднородной генеральной совокупности на типологические или районированные группы по какому-либо существенному признаку, после чего из каждой группы производится случайный отбор единиц.

Для серийной (гнездовой) выборки характерно то, что генеральная совокупность первоначально разбивается на определенные равновеликие или неравновеликие серии (единицы внутри серий связаны по определенному признаку), из которых путем случайного отбора отбираются серии и затем внутри отобранных серий проводится сплошное наблюдение.

Механическая выборка представляет собой отбор единиц через равные промежутки (по алфавиту, через временные промежутки, по пространственному способу и т.д.).

Выборочный отбор может быть повторным и бесповторным. При повторном отборе вероятность выбора любой единицы не ограничена. При бесповторном отборе выбранная единица в исходную совокупность не возвращается.

Для отобранных единиц рассчитываются обобщенные показатели (средние или относительные) и в дальнейшем результаты выборочного исследования распространяются на всю генеральную совокупность.

Основной задачей при выборочном исследовании является определение ошибок выборки. Принято различать среднюю и предельную ошибки выборки.

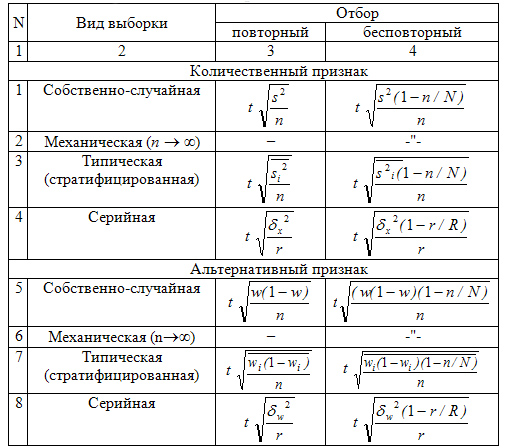
Где - средняя из внутригрупповых выборочных дисперсий для непрерывного признака;

- средняя из внутригрупповых дисперсий доли;

— число отобранных серий, — общее число серий;

,

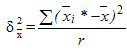где — средняя -й серии;

— общая средняя по всей выборочной совокупности для непрерывного признака;

,

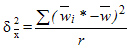где — доля признака в -й серии;

— общая доля признака по всей выборочной совокупности.

Доверительные интервалы для генеральной средней можно установить на основе соотношений

(11.12)

где - генеральная и выборочная средние соответственно; - предельная ошибка выборочной средней.

Доверительные интервалы для генеральной доли устанавливаются на основе соотношений