61. Показатели общего качества регрессионной модели: остаточная сумма квадратов, стандартная ошибка регрессии, коэффициент детерминации, статистическая значимость параметров и регрессии в целом.

Общее качество регрессионной модели оценивается с помощью параметров:

Остаточная сумма квадратов

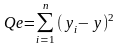
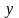, - соответственно фактические и расчетные значения результирующего признака.

Зависит как от единиц измерения у, так и от количества наблюдений.

Стандартная ошибка регрессии

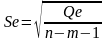
N – количество наблюдений

M – количество объясняющих переменных

Если модель не содержит свободного члена, то ошибка рассчитывается по формуле.

Чем меньше величина S, тем лучше уравнение регрессии описывает независимую переменную Y.

Коэффициент детерминации

Если при достаточно большом n значения коэффициента близко к 1, то это говорит о хорошем качестве регрессии.

Проверка статистической значимости регрессии в целом.

Осуществляется с помощью двух гипотез (проверяется статистическая значимость коэффициента детерминации)

H₀: R² =0

H₁: R² ≠0

Прверка осуществляется с помощью критерия Фишера

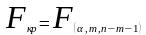- критическая точка распределения Фишера

Если 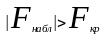, то H₀ отвергается и R² является статистически значим. Следовательно регрессию можно считать статистически значимой в целом, т.е. влияние факторов или переменных x₁, x₂, …., x_m на переменную y в целом существенно.

Статистическая значимость параметров регрессии

Проверяются гипотезы с помощью критерия Стьюдента

H₀: b_i =0

H₁: b_i ≠0

Критерий Стьюдента

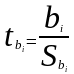
- стандартная ошибка параметра , z_jj – диагональный элемент матрицы

Критическая точка распределения 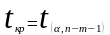распределение Стьюдента

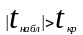, тогда H₀ отвергается, отсюда b_i статистически значим.

Статистическую значимость параметров b_i можно также проверить с помощью доверительных интервалов этих параметров

, где β_i из теоретического уравнения регрессии

Доверительный интервал определяет границы варьирования теоретического значения параметра b_i с вероятностью p = 1-α , где α – уровень значимости

Зависимость величины доверительного интервала от количества наблюдений n от уровень значимости α и стандартной ошибки регрессии S такая же как и в случае парной линейной регрессии, а именно:

а) с увеличением объема выборки доверительный интервал уменьшается

б) при α→0, доверительный интервал увеличивается

в) с увеличением Sе доверительный интервал увеличивается

Доверительный интервал определяет границы варьирования теоретического значения параметра b_i с вероятностью p = 1-α , где α – уровень значимости

Замечание

1. Если некоторый доверительный интервал содержит 0, то соответствующий параметр b_i в уравнении регрессии не является статистически значимым.

2. Из отсутствия значимости каждого из параметров регрессии не следует незначимость регрессии в целом.

3. Если качество построенной регрессии удовлетворено и исходные предпосылки МНК выполняются, то на основе построенного уравнения регрессии можно сделать вывод:

а) значение b_i (i= 1, 2…,m) показывает на сколько единиц в среднем изменяется значение y при увеличении x_i на 1.

б) частные коэффициенты эластичности E_i показывают на сколько процентов изменяется значение переменной y при увеличении x_i на 1%.

в) построенное уравнение регрессии может быть использовано при прогнозировании результатов переменной y при заданных значениях независимых переменных x_i

4. исследование линейной модели множественной регрессии корректно только в случае выполнения исходных предпосылок.

61. Государственные внебюджетные фонды: назначение, формирование, направления, расходования; их социально-экономическая сущность.

Государственный внебюджетный фонд — фонд денежных средств, образуемый вне федерального бюджета и бюджетов субъектов Российской Федерации и предназначенный для реализации конституционных прав граждан на пенсионное обеспечение, социальное страхование, социальное обеспечение в случае безработицы, охрану здоровья и медицинскую помощь. Расходы и доходы государственного внебюджетного фонда формируются в порядке, установленном Бюджетным кодексом России, а также иными законодательными актами, включая законы о бюджете Российской Федерации на соответствующий год.

Государственные федеральные внебюджетные фонды относятся к федеральной собственности. Они имеют социальную, экономическую, благотворительную и другую направленность. Через государственные внебюджетные фонды осуществляется перераспределение части национального дохода в интересах отдельных социальных слоев населения.

Государственные социальные внебюджетные фонды — это целевые централизованные фонды финансовых ресурсов, формируемые за счет обязательных платежей и отчислений юридических и физических лиц и предназначенные для реализации конституционных прав граждан на пенсионное обеспечение, социальное страхование, социальное обеспечение, охрану здоровья и медицинскую помощь.

Внебюджетные фонды решают две важные задачи: обеспечение дополнительными средствами приоритетных сфер экономики и расширение социальных услуг населения. Они помогают решать стоящие перед экономикой задачи обеспечения подъема производства, преодоления временной стагнации и неустойчивости кризисных явлений.

В России действуют следующие государственные социальные внебюджетные фонды:

• Пенсионный фонд Российской Федерации;

• Фонд социального страхования Российской Федерации;

• Федеральный фонд обязательного медицинского страхования.

• Государственный фонд занятости населения Российской Федерации.

К экономическим внебюджетным фондам относятся Федеральный и территориальные дорожные фонды, Фонд воспроизводства минерально-сырьевой базы РФ, Федеральный экологический фонд РФ, Государственный фонд борьбы с преступностью и др.

Существуют также внебюджетные фонды межотраслевого и отраслевого назначения, целью которых является финансовая поддержка конкретных институтов, проектов, развитие и стимулирование производства (например, Федеральный фонд поддержки малого предпринимательства, Фонд содействия научно-техническому прогрессу и др.). Однако такие фонды имеют свою специфику и будут рассмотрены в других главах.

61. Диаграммы как графический метод изображения статистических данных. Их виды.

Наиболее распространенными в статистике графическими методами изображения экономической информации являются диаграммы. Диаграмма — графическое представление данных, позволяющее быстро оценить соотношение нескольких величин. Представляет собой геометрическое символьное изображение информации с применением различных приёмов техники визуализации.

Среди них рассмотрим:

• диаграммы сравнения;

• структурные диаграммы;

• координатные диаграммы и др.

1. Диаграммы сравнения (ДС) применяется для сравнения нескольких величин друг с другом. Диаграммы сравнения отражают соотношения различных исследуемых объектов в связи с каким-либо экономическим показателем. Диаграммы сравнения могут быть столбиковые и ленточные. В столбиковых диаграммах анализируемые величины графически изображаются в виде вертикально расположенных прямоугольников -столбиков). Если прямоугольники расположить не по вертикали, а горизонтально, то диаграмма получит название ленточной. Столбиковые и ленточные диаграммы взаимозаменяемы, так как в обоих случаях используется одно измерение - высота столбиков или длина полосы. Построение столбиковых ленточных диаграмм требует соблюдения ряда правил. Одно из важнейших состоит в соответствии столбиков по высоте, а лент (полос) по длине отображаемым цифрам и принятому масштабу. При построении диаграмм столбики или ленты располагают в убывающем или в возрастающем порядке.

2. Структурные диаграммы (СД) – характеризуют соотношение составных частей анализируемой совокупности. По способу изображения делятся на столбиковые и секторные. В секторных диаграммах структура изображается с помощью разной раскраски секторов круга, отражающих удельные веса отдельных частей, составляющих изучаемую совокупность. С их помощью можно показать динамику структуры при этом строятся столбцы или круги разных размеров соот.разной величине изучаемого признака;

3. Координатные диаграммы – они основаны на системе прямоугольных координат. Использование систем прямоугольных координат целесообразно для графического изображения рядов динамики (изменение показателя во времени). Для их построения в прямоугольной системе координат по оси абсцисс слева направо откладываются отрезки, изображающие последовательно периоды времени, а по оси ординат снизу вверх – анализируемый показатель. На одной и той же диаграмме может быть приведено несколько кривых отражающих изменение изучаемого показателя по нескольким объектам. В этом случае на графике должны быть даны условные обозначения, расшифровывающие к какому объекту относится та или иная линия.

64. Понятие системы в экономическом анализе. Элементы системы, их взаимосвязь между собой и внешней средой.

Система – множество составляющих единство элементов, их связей и взаимодействий между собой и внешней средой

Система есть множество связанных между собой компонентов той или иной природы, упорядоченное по отношениям, обладающим вполне определенными свойствами; это множество характеризуется единством, которое выражается в интегральных свойствах и функциях множества.

Системой называется любой объект, который, с одной стороны, рассматривается как единое целое, а с другой – как множество связанных между собой или взаимодействующих составных частей.

Любой системе присущи целостность, качественная определенность, целенаправленность.

Элемент – неделимая часть системы, обладающая самостоятельностью по отношению к данной системе. Неделимость означает, что не рассматривается внутреннее строение элемента, каждый элемент характеризуется только внешними проявлениями в виде взаимосвязей с другими элементами и внешней средой. Состояние элементов системы в зависимости от различных факторов может изменяться (фактор времени, пространства, внешней среды).

Понятие системы охватывает комплекс взаимосвязанных элементов, действующих как единое целое. В систему входят следующие компоненты:

1. Структура - множество элементов системы и взаимосвязей между ними.

2. Входы и выходы - материальные потоки или потоки сообщений, поступающие в систему или выводимые ею.

3. Закон поведения системы

4. Цель и ограничения.

Среди известных свойств систем целесообразно рассмот­реть следующие – относительность, делимость и целостность.

Свойство относительности устанавливает, что состав эле­ментов, взаимосвязей, входов, выходов, целей и ограничений зависит от целей исследователя. При выделении системы некоторые элементы, взаи­мосвязи, входы и выходы не включаются в нее из-за слабого влияния на остающиеся элементы, из-за наличия самостоя­тельных целей, плохо согласующихся с целью всей системы, и т.д. Они образуют внешнюю среду для рассматриваемой системы.

Делимость означает, что систему можно представить со­стоящей из относительно самостоятельных частей - подсис­тем, каждая из которых может рассматриваться как система. Возможность выделения подсистем (декомпозиция системы) упрощает ее анализ, так как число взаимосвязей между под­системами и внутри подсистем обычно меньше, чем число связей непосредственно между всеми элементами системы. Вы­деление подсистем проводит исследователь, и оно условно.

Свойство целостности указывает на согласованность цели функционирования всей системы с целями функционирования ее подсистем и элементов.

Надо также иметь в виду, что система, как правило, имеет больше свойств, чем составляющие ее элементы. Так, предпри­ятие обладает юридической самостоятельностью, а его под­разделения - нет.