4.3.Расчёт поперечной арматуры
Расчёт поперечной арматуры продольного ребра выполняем аналогично расчёту поперечной арматуры диафрагмы.
1.Проверяем достаточность размеров из условия прочности по наклонной полосе между трещинами:
Исходя из этого:
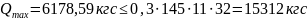
Выполнение этого условия означает, что размеры сечения достаточны.
2.Назначаем шаг хомутов:
Подставляя известные значения, получаем:
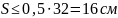
Принимаем
3.Назначаем
хомуты диаметра
Силу, сосредоточенную в хомутах, заменяем условно распределённой на единицу длины элемента силы :
Тогда
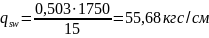
При этом должно выполняться следующее условие:
Принимаем
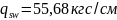
4.Определяем предельную поперечную силу, которая может быть допущена на опоре при заданном армировании
Тогда
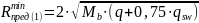
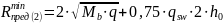
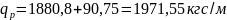
Подставляя ранее найденные значения, получаем:
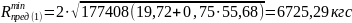
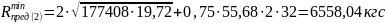
5.Определим значение проекции наклонного сечения С:
Тогда
Принимаем
6.
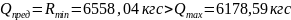
7.В средней трети пролёта, где поперечная сила воспринимается только бетоном можно поставить хомуты с большим шагом:
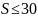
П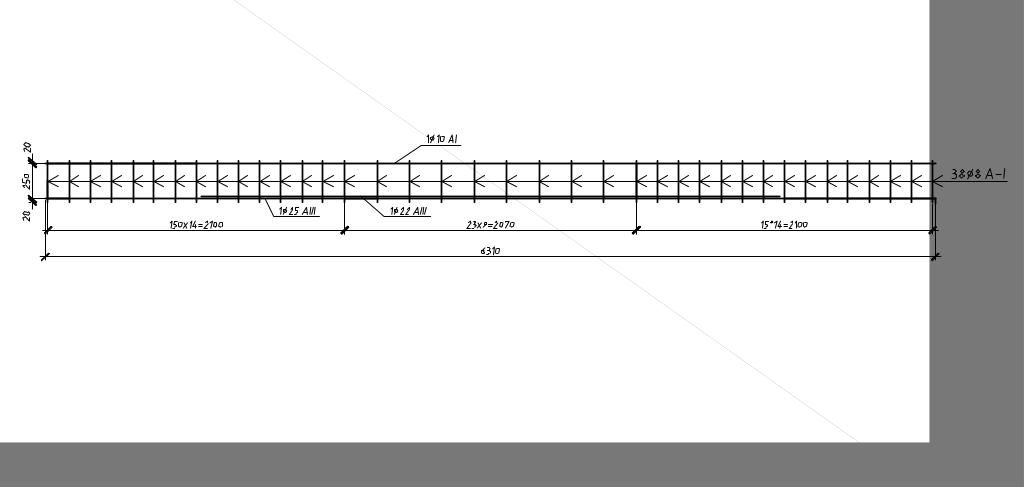
ринимаем
Рис.4.5.
5.Проектирование неразрезного прогона
5.1.Статический расчёт и построение огибающих эпюр моментов
Неразрезные прогоны жестко связаны с колоннами и образуют с ними рамную конструкцию. Достоинством неразрезного прогона является более выгодная статическая работа и, соответственно, более рациональное распределение арматуры, а также более высокая жесткость. Недостатком такого прогона является сложность осуществления жестких стыков.
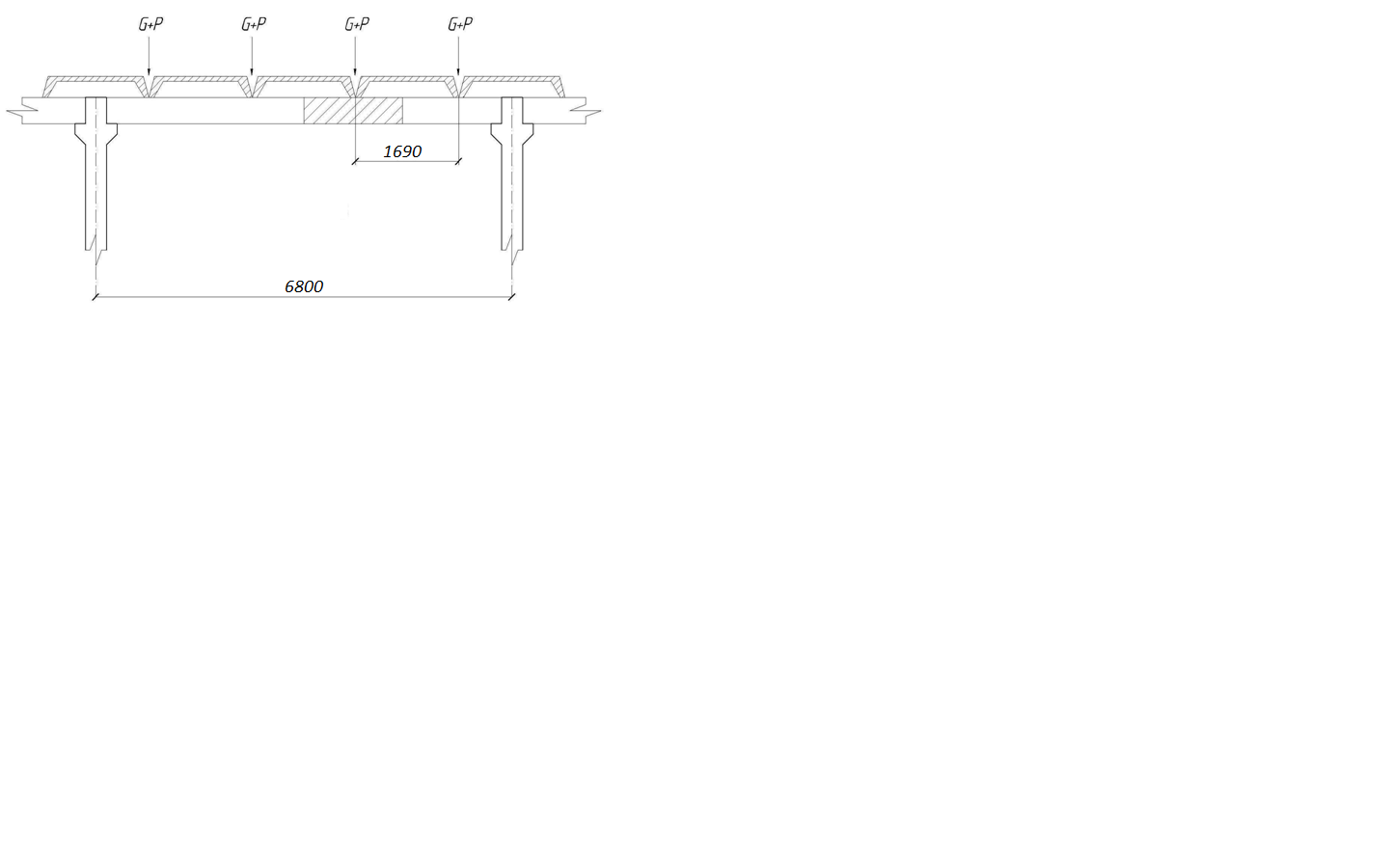
Рис.5.1.
Верхнюю арматуру пропускают через пазы колонны. В этом случае она может воспринимать изгибающий момент. Нагрузки на прогон передаются в виде постоянных и временных сосредоточенных сил G и P, а также равномерно распределенной нагрузки от собственного веса в местах опирания продольных ребер панели (плиты, диафрагм, продольных ребер) и собственного веса участка прогона длиной, равной ширине панели. Таким образом, расчетная постоянная нагрузка равна:
Где
-
составляющая силы G
от веса пола
-
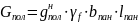
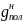нормативная постоянная нагрузка от
веса пола на
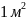перекрытия,
-
нормативная постоянная нагрузка от
веса плиты
-
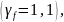
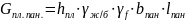
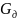нормативная постоянная нагрузка от
веса диафрагм панели
m-число диафрагм в одной панели,
-
нормативная постоянная нагрузка от
веса продольных ребер
2 – число ребер,
-
нормативная постоянная нагрузка от
собственного веса части прогона
Для определения собственного веса прогона высоту прогона определяем как:
Принимаем
Тогда,
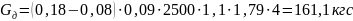
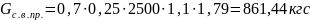
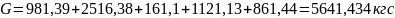
Расчетную полезную сосредоточенную силу определяем по зависимости:
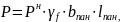
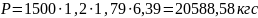
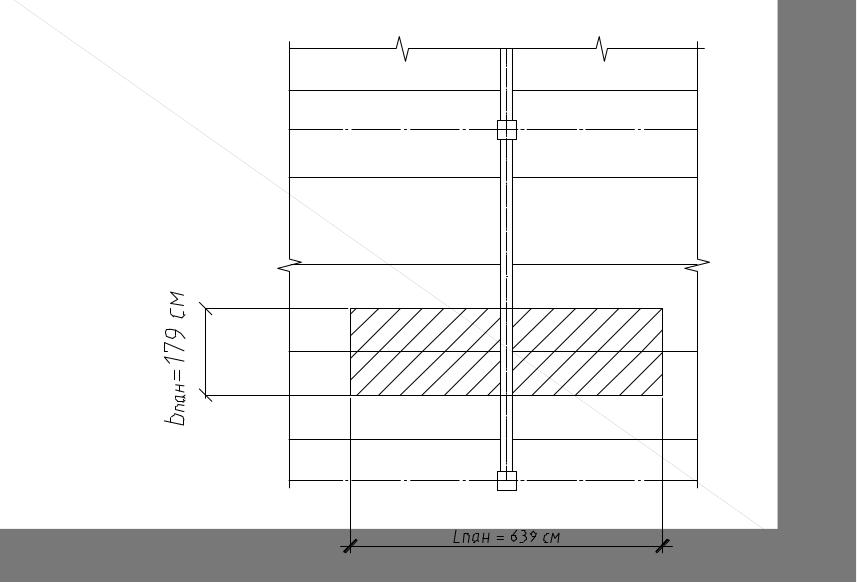
Рис.5.2.
Так как число сосредоточенных сил в пролете больше трех, то нагрузку на прогон можно привести к равномерно распределенной:
Рис.5.3.
Расчетными
пролетами неразрезного прогона для
средних балок принимаются расстояния
между осями колонн
а для крайних – расстояние между осью
колонны и серединой глубины заделки
балки (прогона) в стену.
Установив
расчетную схему с учетом невыгоднейшего
загружения временной нагрузкой, можно
определить значения изгибающих моментов
М в неразрезном прогоне с равными
пролетами или пролетами, отличающимися
друг от друга не более чем на
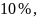с помощью таблицы [1, прил IV]
.
При
действии на прогон равномерно
распределенной нагрузки
и
значения изгибающих моментов М
определяются по формулам:
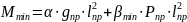
где
- табличные коэффициенты [1, прил. IV].
Результаты расчетов сводим в таблицу:
|
|
|
|
|
|
|
|
|
0,2 |
0,0589 |
9,62 |
0,0695 |
-0,0105 |
41,44 |
-6,26 |
51,06 |
3,36 |
0,4 |
0,0779 |
12,73 |
0,0989 |
-0,0211 |
58,97 |
-12,58 |
71,70 |
0,15 |
0,6 |
0,0568 |
9,28 |
0,0884 |
-0,0316 |
52,71 |
-18,84 |
61,99 |
-9,56 |
0,8 |
-0,0042 |
-0,69 |
0,0381 |
-0,0423 |
22,72 |
-25,22 |
22,03 |
-25,91 |
0,9 |
-0,0497 |
-8,12 |
0,0183 |
-0,068 |
10,91 |
-40,55 |
2,79 |
-48,67 |
1,0 |
-0,1053 |
-17,20 |
0,0144 |
-0,1196 |
8,59 |
-71,31 |
-8,62 |
-88,52 |
1,1 |
-0,0576 |
-9,41 |
0,014 |
-0,0717 |
8,35 |
-42,75 |
-1,06 |
-52,16 |
1,2 |
-0,02 |
-3,27 |
0,03 |
-0,05 |
17,89 |
-29,81 |
14,62 |
-33,08 |
1,4 |
0,0253 |
4,13 |
0,0726 |
-0,0474 |
43,29 |
-28,26 |
47,42 |
-24,13 |
1,5 |
0,0328 |
5,36 |
0,0789 |
-0,0461 |
47,05 |
-27,49 |
52,40 |
-22,13 |
1,6 |
0,0305 |
4,98 |
0,0753 |
-0,0447 |
44,90 |
-26,65 |
49,88 |
-21,67 |
1,8 |
-0,0042 |
-0,69 |
0,0389 |
-0,0432 |
23,19 |
-25,76 |
22,51 |
-26,44 |
1,9 |
-0,0366 |
-5,98 |
0,028 |
-0,0646 |
16,70 |
-38,52 |
10,72 |
-44,50 |
2,0 |
-0,0799 |
-13,05 |
0,0323 |
-0,1112 |
19,26 |
-66,30 |
6,21 |
-79,36 |
2,1 |
-0,0339 |
-5,54 |
0,0293 |
-0,0633 |
17,47 |
-37,74 |
11,93 |
-43,28 |
2,2 |
0,0011 |
0,18 |
0,0416 |
-0,0405 |
24,80 |
-24,15 |
24,98 |
-23,97 |
2,4 |
0,0411 |
6,71 |
0,0855 |
-0,0385 |
50,98 |
-22,96 |
57,70 |
-16,24 |
2,5 |
0,0461 |
7,53 |
0,0895 |
-0,0395 |
53,37 |
-23,55 |
60,90 |
-16,02 |
По
результатам вычислений строим огибающие
эпюры
(рис. 5.4)
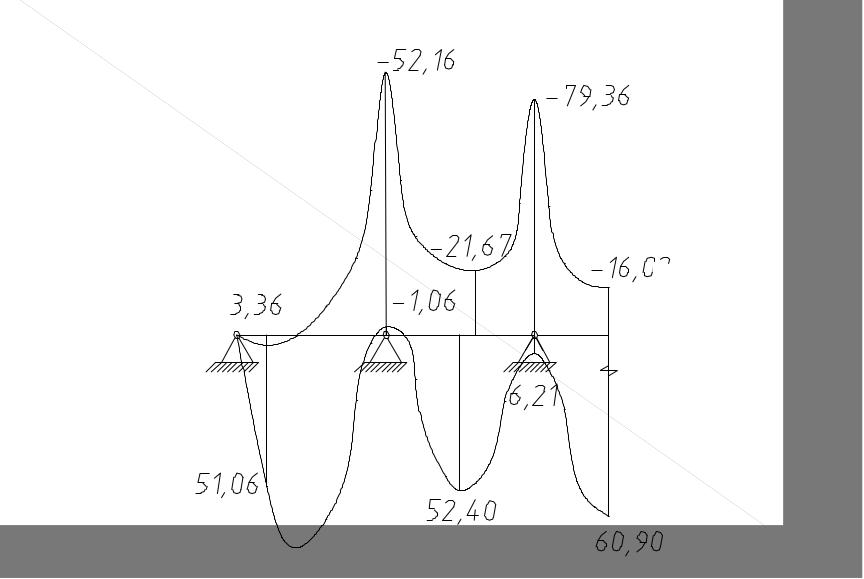
Рис.5.4.