3.3. Расчёт поперечной арматуры

Поперечная арматура ставится в балках для обеспечения их прочности по наклонным сечениям. Будем выполнять ее в виде хомутов. Задача расчета поперечной арматуры состоит в подборе диаметра и шага хомутов.

1. Проверяем достаточность размеров из условия прочности по наклонной полосе

Исходя из этого,

Выполнение этого условия означает, что размеры сечения достаточны.

2. Назначаем шаг хомутов:

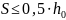
Подставляя известные значения, получаем:

Принимаем

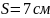
3. Назначаем хомуты минимального диаметра А_sw=0,283 см², R_sw=1750 кгс/см².

Силу, сосредоточенную в хомутах заменяем условно распределенной на единицу длины элемента силой :

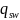Тогда,

При этом должно выполняться следующее условие:

Принимаем

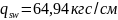
4. Считаем в запас прочности, что 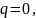так как нагрузка не является равномерно распределенной.

5. Определяем момент :

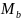Тогда,

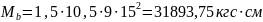
6. Проверяем выполнение следующего условия:

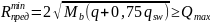
Подставляя ранее найденные значения, получаем:

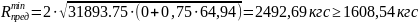
При этом значение проекции наклонного сечения C:

7. Так как то окончательно принимаем хомуты с шагом S=7 см, А_sw=0,283 см².

4.Проектирование продольного ребра

4.1.Статический расчёт

Продольные ребра рассматриваются как свободно опертые балки. Нагрузка на них передается непосредственно от плиты по закону треугольников или трапеций и от диафрагм в виде сосредоточенных сил.

В этом случае расчетная схема продольного ребра выглядит следующим образом;

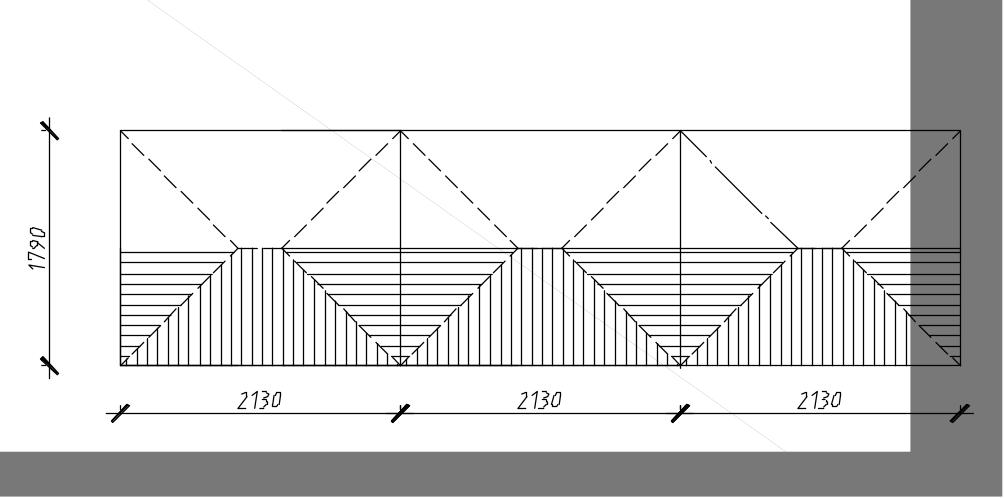
Рис.4.1.Схема загрузки продольного ребра (грузовая площадь)

1.Определим нагрузку от собственного веса погонного метра ребра:

где – осредненная ширина сечения ребра (

- удельный вес железобетона (

– коэффициент перегрузки (

Тогда

2.Определим значение нагрузки :

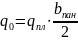
Тогда

Практически нагрузку принимают равномерно распределенной:

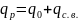
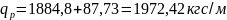
Наибольший изгибающий момент в середине пролета определяется как:

Наибольшая поперечная сила на опорах определяется как:

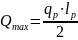
Пролёт 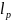принимается равным:

где b_пр принимаем равным 25 см.

Таким образом:

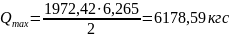
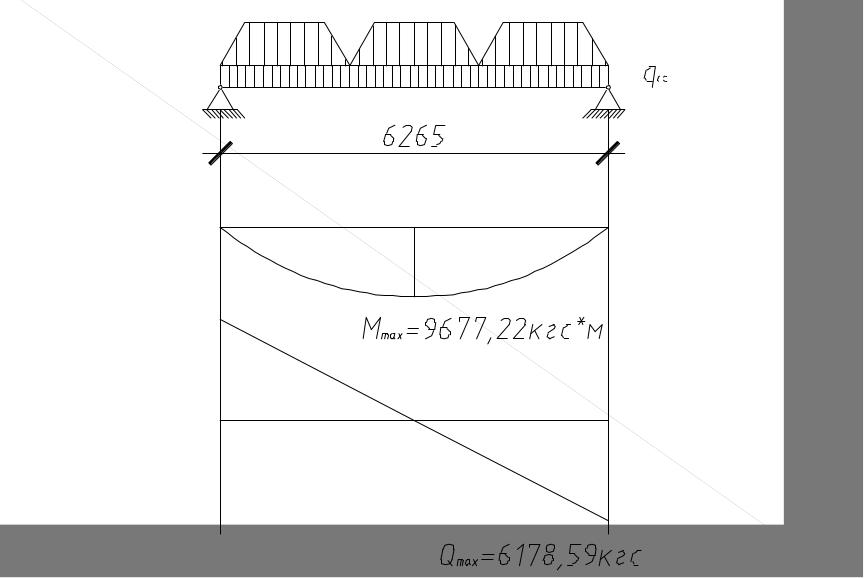
Рис.4.2.

Рис.4.3.

4.2.Расчёт продольной арматуры

При расчете арматуры в ребре необходимо учесть работу плит, часть которых попадает в сжатую зону. Расчетный профиль зависит от положения нейтральной оси. Так как она проходит в полке, то сечение рассчитывается как прямоугольное с шириной .

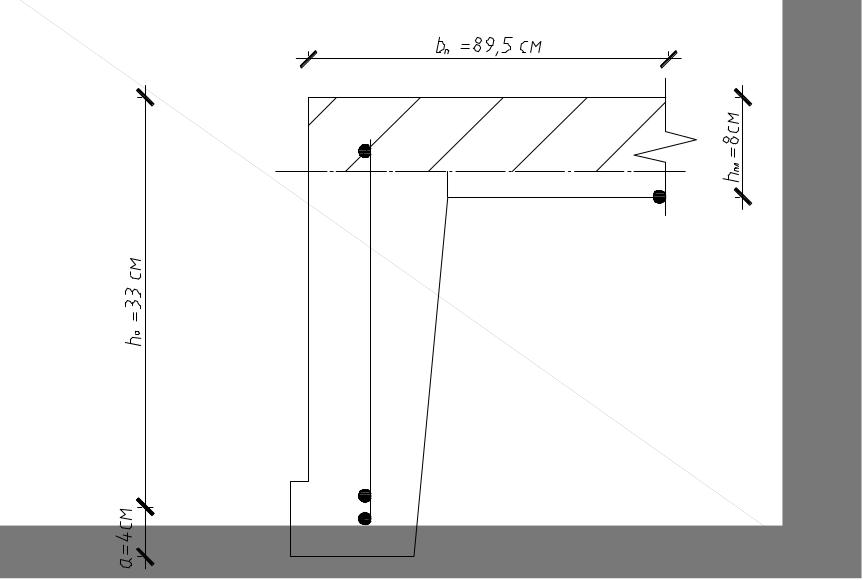
Рис.4.4.

1.Назначаем полезную высоту сечения по следующей зависимости:

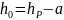
Тогда:

– расстояние от центра тяжести арматуры до верхней кромки.

2.Назначаем расчетную ширину полки , исходя из следующих условий:

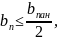
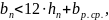
Тогда

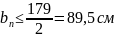
Выбираем

3.Определяем положение нейтральной оси:

Подставляя найденные ранее значения, получаем:

Так как , то нейтральная ось проходит в полке, и сечение рассчитывается как прямоугольное с шириной

4.Вычисляем параметр

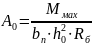
Тогда

По таблице для найденного параметра определяем коэффициент

5.Определяем площадь сечения продольной арматуры:

Исходя из этого:

6.Подбираем по сортаменту:

A_{s факт}=8,71 см²

Верхний продольный стержень назначаем конструктивно из арматуры класса А-I  10 кл.