8.3.Модификации методов Ньютона и Ньютона – Рафсона

Модификации методов обусловлены следующими реальными проблемами:

1. большой объём вычислений на каждой итерации метода при оценке матрицы ;

2. отсутствие или потеря положительной определённости матрицы .

Модификация 1.Представляется итерационной схемой

(8.3.1)

где целое число, меньшее или равное .

При получаем метод Ньютона, а при упрощённый метод Ньютона, в котором гессиан вычисляется только в точке .

Модификация 2. Представляется итерационной схемой

(8.3.2)

где для оценки приемлемого шага Канторовичем предложен алгоритм:

шаг 1. ;

шаг 2. вычислить ;

шаг 3. если , то и перейти на шаг 2, иначе поиск окончен.

Модификация 3. Представляется итерационной схемой регуляризованного метода Ньютона

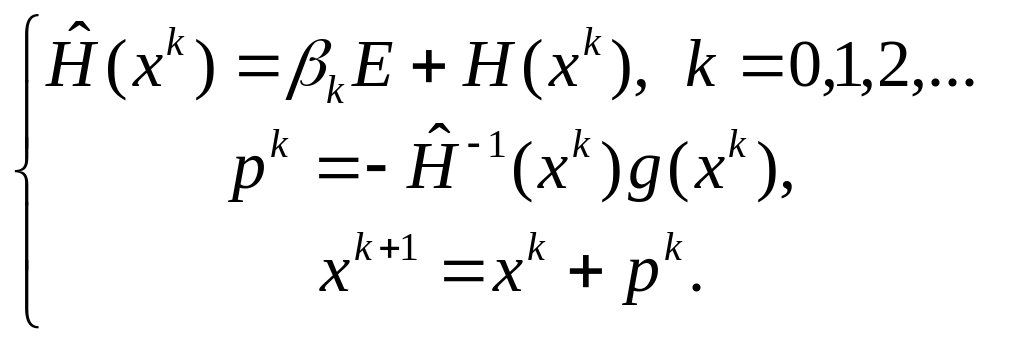(8.3.3)

где оценивание параметра , например, по формуле , , продолжается до тех пор, пока матрица не станет положительно определенной.

Модификация 4. Представляется итерационной схемой регуляризованного метода

(8.3.4)

где параметр обеспечивает положительную определенность матрицы .

Модификация 5. Представляется итерационной схемой регуляризованного метода

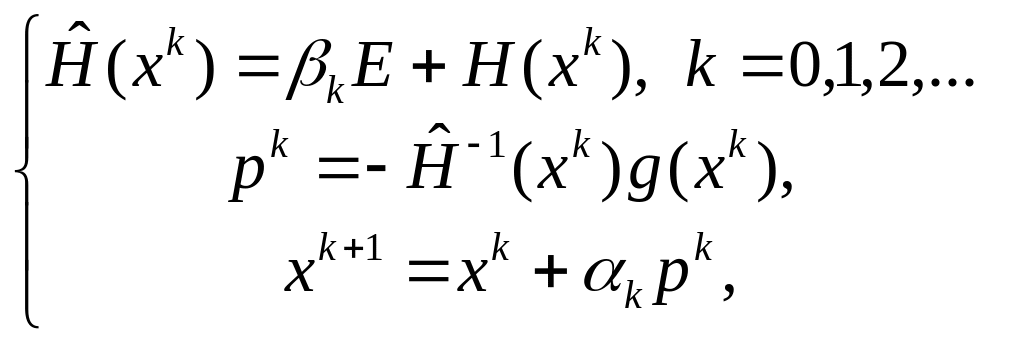(8.3.5)

где параметр обеспечивает положительную определенность матрицы , а оценивание шага отвечает концепция спуска с малым шагом, приведённой в разделе 6.3.

Модификация 6. Разработана Гринстадтом(Greenstadt,1967) на основе спектральной факторизации неположительно определенной матрицы Гессе.

Представляется алгоритмом оценки корректного направления :

шаг 1. выполняется спектральная факторизация матрицы Гессе

и

оцениваются ортогональная матрица , т.е. , столбцами которой являются собственные векторы, и диагональная матрица , образованная из собственных чисел;

шаг 2. из абсолютных величин собственных значений матрицы формируется матрица ;

шаг 3. вычисляется положительно определенная матрица

;

шаг 4. оценивается направление поиска

(8.3.6)

и работа алгоритма завершается.

Модификация 7. Разработана Гиллом и Мюрреем (Gill,Murray,1974) на основе факторизации Холесского неположительно определенной матрицы Гессе.

Представляется алгоритмом оценки приемлемого направления :

шаг 1. выполняется факторизация Холесского матрицы

: ,

где есть диагональная матрица с неотрицательными диагональными элементами, равными нулю, если положительно определена;

шаг 2. проверяется условие и если оно выполнено, то полагается

и работу алгоритма завершается; иначе следует перейти на шаг 3;

шаг 3. следуя теореме о “кругах” Гершгорина (Дэннис,Шнабель,1988), вычисляется первая

верхняя граница для параметра в представлении регуляризованной матрицы

;

шаг 4. вычисляется вторая верхняя граница для

;

шаг 5. оцениваются параметр

,

направление поиска

(8.3.7)

и работа алгоритма завершается.