7.4.3.Основные соотношения метода сопряженных градиентов Флетчера-Ривса

1.Из разложения (7.4.4) и квадратичной определяется взаимосвязь векторов и , а именно

,

и

. (7.4.8)

2.Так как есть вектор-градиент в точке минимума функции в направлении , то

, (7.4.9)

Покажем, что . Учитывая (7.4.9) имеем

Тогда

.

3.Так как векторы и сопряжены, то имеем важное соотношение

, (7.4.10)

Использую соотношения (7.4.9) и (7.4.10), можно получить новое представление :

. (7.4.11)

Соотношения (7.4.2), (7.4.5) и (7.4.7) - (7.4.11) отражают взаимосвязи векторов , , и определяют принципиальный алгоритм метода сопряженных градиентов.

7.4.6.Траектория поиска и некоторые выводы

Траектория поиска минимума может иметь, например, следующий вид (Рис.7.3)

Анализ взаимосвязи последовательностей векторов , и показывает, что направления строятся с помощью процедуры образования - сопряженных векторов, использующей векторы , а градиенты строятся ортогонализацией векторов .

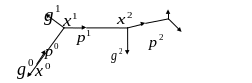
Рис.7.3.

7.4.7.Модификации метода сопряжённых градиентов

Модификации метода обусловлены необходимостью его применения для минимизации функций общего вида и различаются методами оценивания:

1. параметра сопряжения ;

2. вектора направления ;

3. шага .

Модификации параметра сопряжения , наряду с оценкой (7.4.3), представляются оценками

(7.4.12)

и

. (7.4.13)

Результатом большого количества численных экспериментов явился вывод о предпочтительности оценки (7.4.13) (Бертсекас,1987).

Модификации вектора направления обусловлены тем фактом, что под влиянием неквадратичных составляющих может произойти потеря сопряжённости направлений.

Так, в случае, когда число переменных велико, часто оказывается, что после ряда итераций метод начинает генерировать направления, движение вдоль которых неэффективно. В связи с этим, процесс построения сопряжённых направлений (7.4.2) целесообразно вести циклами, начиная каждый цикл с направления наискорейшего спуска .

Такое периодическое восстановление метода называется рестартом.

Основными правилами выбора моментов рестарта являются:

1. рестарт через каждые итераций;

2. рестарт через итераций или, если это произойдёт раньше, при выполнении условия

.

Модификации оценивания шага отличаются требованиями к точности численной оценки . Детальные численные исследования показали высокую эффективность метода при высокой точности оценки . Однако, очень точное решение соответствующей задачи одномерной минимизации, например, регуляризованным методом Брендта, порождает большой объём вычислений. Поэтому рациональным компромиссом представляется реализация метода с машинно точным оцениванием шага при ограничении допустимого числа итераций.