
- •5. Поисковая минимизация
- •5.1.Метод покоординатного спуска Гаусса-Зейделя (Gauss - Seidel)
- •5.2.Метод конфигураций Хука – Дживса (Hooke - Jeeves)
- •7. Градиентные методы
- •7.1.Градиентный метод
- •7.1.1.Итерационная схема метода
- •7.1.2.Основные модификации метода
- •7.2.Оптимальный градиентный метод
- •7.2.1.Итерационная схема метода
- •7.2.2.Анализ сходимости метода
- •7.2.3.Траектория поиска
- •7.2.4.Выводы
- •7.4.Метод сопряженных градиентов
- •7.4.1.Оценивание направления поиска
- •7.4.2.Оценивание шага
- •7.4.3.Основные соотношения метода сопряженных градиентов Флетчера-Ривса
- •7.4.6.Траектория поиска и некоторые выводы
- •7.4.7.Модификации метода сопряжённых градиентов
- •8. Ньютоновские методы
- •8.1.Методы Ньютона и Ньютона-Рафсона
- •8.2.Скорость сходимости методов Ньютона и Ньютона - Рафсона
- •8.3.Модификации методов Ньютона и Ньютона – Рафсона
- •8.4.Некоторые результаты и выводы
- •10. Методы штрафных и барьерных функций
- •10.1.Методы преобразования
- •10.2.Условия Куна - Таккера
- •10.3.Барьерные функции
- •10.3.1.Функция барьера
- •10.3.2.Сходимость методов барьерных функций
- •10.3.5.Многократная безусловная минимизация
- •10.3.6.Проблемы применения барьерных методов
- •10.4.Штрафные функции
7.2.2.Анализ сходимости метода
Анализ
сходимости метода
показывает, что при
![]() ,
направление
,
направление![]() будет направлением убывания
будет направлением убывания![]() ,
т.к.
,
т.к.
![]() ,
причём угол между
,
причём угол между
![]() и
и
![]() всегда далёк от прямого.
всегда далёк от прямого.
Поэтому
комбинация любого из рассмотренных
методов выбора шага
и
![]() даёт глобально
сходящийся алгоритм безусловной
минимизации.
даёт глобально
сходящийся алгоритм безусловной
минимизации.
7.2.3.Траектория поиска
Траектория поиска для двумерной квадратичной функции может быть следующей (Рис 7.1)
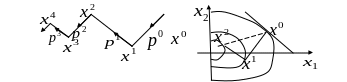
а) б)
Рис.7.1.
Легко
заметить, что смежные направления поиска
ортогональны, при этом вектор![]() параллелен
вектору
параллелен
вектору
![]() ,
а вектор
,
а вектор![]() параллелен вектору
параллелен вектору
![]() ,
и т.д.
,
и т.д.
Этот результат является основой метода параллельных касательных, применение которых позволяет несколько ускорить оптимальный градиентный метод.
7.2.4.Выводы
Анализ итерационной схемы и скорости сходимости метода, а также траектории движения к стационарной точке , позволяет сформулировать три основные группы выводов.
1.В
малой окрестности точки
оценки
![]() начинают приближаться к нулю. Поэтому
на точности оценивания
начнёт все более сказываться точность
оценивания шага
.
А из этого следует подтверждённый
практикой вывод: в
окрестности стационарной точки
оптимальный градиентный метод
неэффективен.
начинают приближаться к нулю. Поэтому
на точности оценивания
начнёт все более сказываться точность
оценивания шага
.
А из этого следует подтверждённый
практикой вывод: в
окрестности стационарной точки
оптимальный градиентный метод
неэффективен.
Поэтому при замедлении поиска рационально переключиться на другие методы, в частности, квадратичной аппроксимации в окрестности точки каждого очередного приближения.
2.Продвижение к точке по ортогональным направлениям приводит к выводу о быстрой сходимости метода в случае, когда линии уровня целевой функции подобны эллипсам, причем, чем ближе геометрия эллипсов к соответствующим концентрическим окружностям, тем лучше. Этот вывод надежно подтверждён практикой и отражает сильное влияние на скорость сходимости масштаба компонент вектора .
Поэтому медленный поиск свидетельствует, как правило, о плохо отмасштабированной задаче оптимизации и следует либо изменить масштаб компонент вектора , либо перейти к более сложным методам решения плохо отмасштабированных задач оптимизации.
3.Несмотря на глобальную скорость сходимости метода, его эффективность является низкой и, следовательно, противоречит его исторически сложившемуся названию наискорейшего спуска.
7.4.Метод сопряженных градиентов
7.4.1.Оценивание направления поиска
Векторы
направления
![]() оцениваются следующим образом:
оцениваются следующим образом:
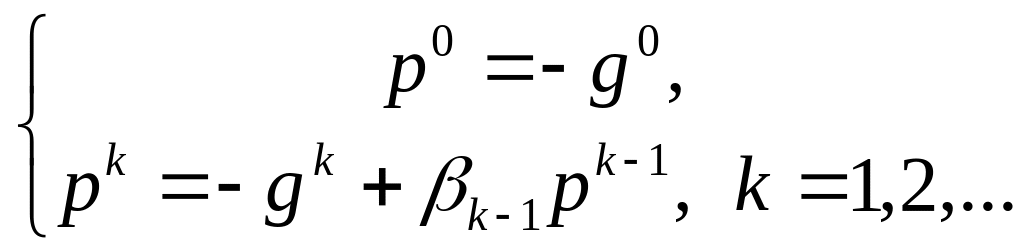 (7.4.2)
(7.4.2)
где
скаляр
![]() определяется так, чтобы сделать вектор
определяется так, чтобы сделать вектор
![]() сопряженным
с вектором
сопряженным
с вектором![]() .
Для этого учтём, что
.
Для этого учтём, что
![]() ,
,
и, следовательно, получим
![]() .
(7.4.3)
.
(7.4.3)
7.4.2.Оценивание шага
В случае, когда квадратичная, оценить шаг можно аналитически. Действительно, для квадратичной целевой функции имеем строгое равенство в разложении
![]() .
(7.4.4)
.
(7.4.4)
Выберем следующую точку
![]() (7.4.5)
из условия
(7.4.5)
из условия
![]() .
(7.4.6)
.
(7.4.6)
Для этого дифференцируя (7.4.4) по и приравнивая производную нулю, имеем
![]() ,
,
а значит
![]() .
(7.4.7)
.
(7.4.7)
При неквадратичной , для оценки нужно использовать численный одномерный поиск.
