Курс
лекций: Методы оптимизации
5. Поисковая минимизация
5.1.Метод покоординатного спуска Гаусса-Зейделя (Gauss - Seidel)
Выполнение
метода начинается с выбора начальной
точки
,
длины шага
и параметра критерия окончания поиска
.
Стратегия
метода включает
покоординатный цикл
,
при реализации для каждой
координаты независимой переменной
двух этапов поиска:
решение задачи одномерной минимизации
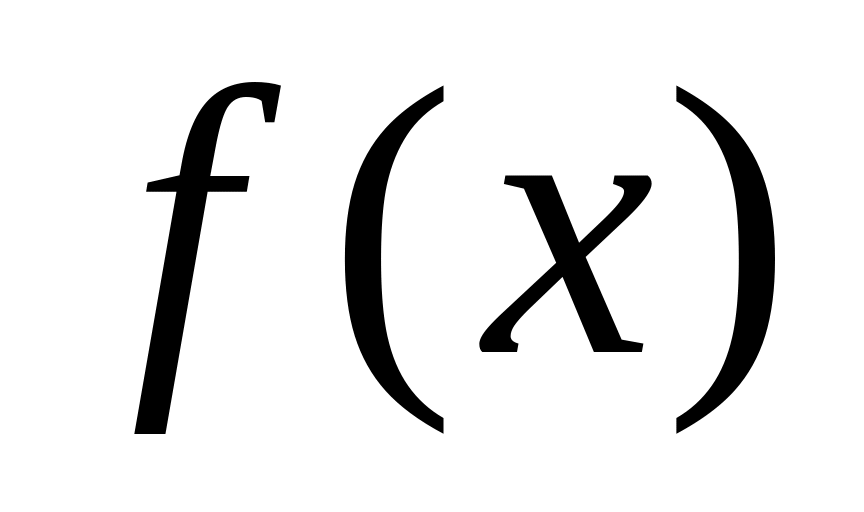по
координате при фиксированных значениях
остальных координат, т.е. оценивание
,
;
(5.1.1)
замену прежнего значения координаты на её оптимальное значение, т.е.
.
(5.1.2)
В
результате
кратной
покоординатной минимизации
получаем
оценку
точки локального минимума
,
качество приближения которой проверяем
с помощью критерия
.
(5.1.3)
Выполнение
этого критерия означает достижение
- сходимости процесса минимизации
и окончание поиска. В противном случае,
следует уменьшить шаг поиска, например
в форме
переопределить
:
,
и
повторить покоординатный поиск, проверку
критерия (5.1.3) и т.д.
Схематически метод Гаусса-Зейделя можно представить в виде (Рис.5.1)
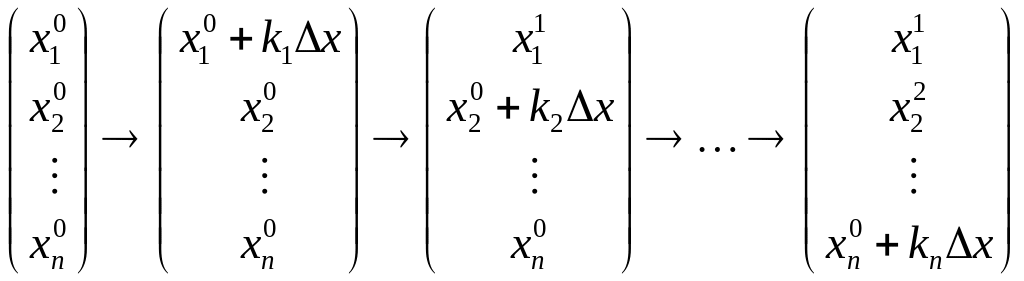
Рис.5.1.
В
верхней части рис.5.1 приведены
последовательные точки
,
генерируемые методом за один
шаговый
цикл. В нижней - критерий окончания
поиска и операции, необходимые для
перехода к следующему циклическому
поиску и проверке критерия (5.1.1).
Анализ траектории поиска показывает, что поскольку каждое звено траектории поиска параллельно одной из координатных осей, то траектория поиска по двум независимым переменным может походить на “лестницу”.
Рассмотрим качественные аспекты решения методом Гаусса-Зейделя большинства реальных задач минимизации на примере возникающих при этом трёх основных траекторий поиска.
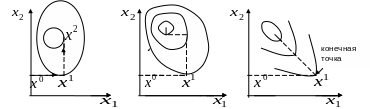
а) б) в)
Рис.5.2.
Наиболее эффективен метод в случае (Рис.5.2.а)), когда линии уровня представляют собой окружности или эллипсы, главные оси которых параллельны координатным осям.
В случае (Рис.5.2.б)) главные оси линий уровня не параллельны координатным осям и при поиске локального минимума нужно многократно менять направление поиска на ортогональное
Третий
случай (Рис.5.2.в)) наиболее сложен. Ясно
видно, что поиск нужно вести по
диагональному относительно координатных
осей направлению. Поскольку это
практически невозможно, то метод
малопригоден. Отметим, что данный случай
обычно означает присутствие в целевой
функции линейно связанных координат
переменной
,
например в форме члена
,
и часто встречается в задачах идентификации
и оптимального управления.