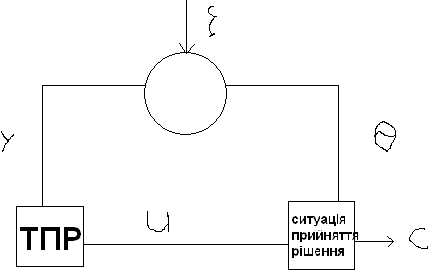
- •Система прийняття рішень. Загальна задача прийняття рішення.
- •2. Параметричні і непараметричні рішення. Приклади. Матрична та лотерейна моделі ситуації.
- •Непараметричні ситуації прийняття рішень. Приклади.
- •3. Еквівалентність матричної та лотерейної схем ситуації.
- •Еквівалентність матричної та лотерейної моделей стохастичної ситуації (перенесення даних про невідоме).
- •Експерименти у системі рішення та їх математичні моделі. Приклади.
- •Той хто приймає рішення та його математична модель. Класи тпр.
- •Теорема існування невизначеності у системі рішення.
- •Прийняття рішення при повній невизначеності. Чотири критерії.
- •Ф ункція корисності (втрат). Лінійна функція корисності. Невід’ємна ф-я втрат.
- •10. Теорема фон Неймана-Моргенштерна про очікувану корисність
- •11. Теорема Севіджа про суб’єктивну імовірність.
- •12. Увігнуті та опуклі функції, Нерівність Йенсена. Баєсів ризик.
- •Байєсівський ризик
- •Рандомізація у теорії ігор та теорії рішень.
- •Доцільність спостережень у стохастичній системі рішень. Плата за спостереження.
- •Методи побудови вирішуючих функцій.
- •Лема Неймана –Пірсона.
- •18. Багатокрокова задача рішення. Звідність до послідовності однокрокових
- •19.Принцип оптимальності Белмана. Алгоритм стохастичного динамічного програмування.
- •20. Розвиток методів і систем ппр
- •21. Ретроспективний аналіз еволюції інформаційних технологій та інформаційних систем.
- •22. Організаційно-технологічні основи прийняття рішень
- •23. Класифікація систем підтримки прийняття рішень (сппр) класифікація сппр
- •24. Базові компоненти сппр
- •25. Стратегія оцінювання і вибору методів підтримки прийняття рішень.
- •26. Створення, впровадження та оцінювання сппр.
- •27. Засоби штучного інтелекту в сппр.
- •28. Сппр на основі сховища даних olar-технологій.
- •29. Групові сппр.
- •30. Виконавчі інформаційні системи.
Методи побудови вирішуючих функцій.
Побудова байєсівських вирішуючих функції екстенсивним методом
Нехай маємо умову:
Задача:
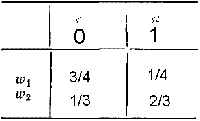
знайти, при якому розподілі величини ω1 та ω2 рішення d1 (ω2) , буде байєсівським d*.
Розв"язок:
визначимо розподіли ω1 та ω2:
P(ω1) = ξ P(ω2) = 1-ξ
1)
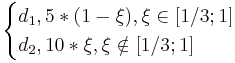
значення експериментів y1, y2 спостереження випадкової величини w1, w2:
Побудова байєсівських вирішуючих функцій нормальним методом.

Апріорний розподіл - розподіл на Ω, який відомо до експерименту.
Апостеріорний розподіл - умовний розподіл на Ω за умови, що ми спостерігали .
Апостеріорний розподіл дає нам додаткову інформацію про параметр і може зменшити байєсівський ризик.
Формула Байєса для обчислення апостеріорного розподілу

ξω(X)=
-ймовірність настання параметра ω, якщо спостерігали .
Лема Неймана –Пірсона.
Нехай
і
 - задані постіними, і
- задані постіними, і
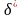 -рішаюча
функція така що
-рішаюча
функція така що
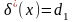 ,
якщо
,
якщо
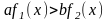
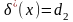 якщо
якщо

У
випадку якщо
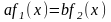 в якості
можна взяти будь-яке значення.
в якості
можна взяти будь-яке значення.
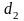 або
або
 .
.
Тоді для будь-якої рішаючої функції
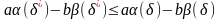
Доведення.
Якщо
- інша рішаюча функція, то нехай
 і
і
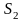 підмножини виморочного простору
підмножини виморочного простору
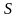 ,
і визначаються наступним чином:
,
і визначаються наступним чином:

Тоді
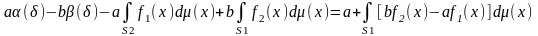
Оскільки
будь-яка рішаюча функція задається
указанням множини
,
на якій вона приймає значення
,
то знаходження рішаючої функції
мінімізуючої
лінійну комбінацію
 ,
рівносильно визначенню множини
,
для якої останній інтеграл приймає
найменше значення. Цей інтеграл досягає
мінімуму , коли множина
включає всі точки
,
рівносильно визначенню множини
,
для якої останній інтеграл приймає
найменше значення. Цей інтеграл досягає
мінімуму , коли множина
включає всі точки
 ,
для яких інтегральна функціє набуває
відємного знаку, і не включає тих точок
в яких підінтегральна функція додатня.
При цьому не грає ролч чи входять точки
рівні 0. Рішаючи функція
,
визначена за допомогою множини
задовільняю
умови 2 і 3.
,
для яких інтегральна функціє набуває
відємного знаку, і не включає тих точок
в яких підінтегральна функція додатня.
При цьому не грає ролч чи входять точки
рівні 0. Рішаючи функція
,
визначена за допомогою множини
задовільняю
умови 2 і 3.
18. Багатокрокова задача рішення. Звідність до послідовності однокрокових
багатокрокова задача рішення - задача, в яких ТПР в одній і тій самій ситуації приймає кожен раз рішення.(не однокрокова задача рішення, де ситуація кожен раз різна).
Основні характеристики БЗР:
відсутність пам"яті (ситуація не залежить від часового параметру, тобто одиницею часу є рішення)
вплив попередньої дії (та стану, в якому перебувала природа) на стан природи на наступному кроці
M=(Θ, U, L(.,.), P(θ))
Py1, y2, ... yN-1(Θ) , Θ - константа, U - дія, Х - втрати, N - кроки, φ(xk, Uk-1)= xk+1 - втрати на наступному кроці (xk+1) залежать від попередньої дії (Uk-1)
g(xk, Uk) -
Багатокрокова
задача прийняття рішення це задача у
котрій на кожному кроці приймається
рішення. Взагалі майже у всіх таких
задачах ставиться за мету знайти краще
кінцеве рішення, яке можна представити
як вектор усіх проміжних рішень. У
термінах динамічного програмування
рішення - це керування. Приймаючи поточне
рішення ми можемо спиратись на результат
минулого рішення для того щоб зробити
кращій вибір. Для стохастичного ДП ми
можемо разглядати ризик як цільову
функцію. Тобто на кожному кроці треба
мінімізувати ризик. Крок у таких задачах
це перехід від одного стану в інший
(наступний) : S(t) -> S(t+1). Рішення - це вибір
у котрий стан перейти. Стан (стан
середовища) - визначається постановкою
задачі. Динаміка полягає в тому що
приймаючи поточне рішення ми спираємось
тільки на результат минулого(або
скінченної кількості минулих) і згідно
з цього рез-та вибираємо краще рішення
на поточному кроці. Поточний вибір не
впливає на попередні а також на наступні.
Ми робимо локальне рішення.