13. Рандомізація у теорії ігор та теорії рішень.

В задачах рішення часто буває дійсним припущення, що рішення d є D вибирається за допомогою додаткової процедури, наприклад, підкидаючи монету. Тобто, приймається змішане рішення – спочатку рішенням приписуються ймовірності, а тоді, згідно з цими ймовірностями, вибирається одна з них.

В таких випадках, втрати цього рішення, згідно з припущенням про середню корисність будуть вираховуватися так: L(w,d)=SUM_{_i=1}^INF [p_i * L(w,d_i)]. (1)

Якщо простір подій незліченний, то рандомізовані рішення можна позначати більш загально – якийсь розподіл на сігма-алгебрі, підмножин множини D.

Рандомізовані рішення позначаються М. тоді зрозуміло, що чисті рішення входять в рандомізовані (D є M): вистачає поставити ймовірності при всіх рішеннях 0, крім того, яке ми хочемо подати. (якщо є D={d₁,d₂,d₃}, то рішення m є M подається як (m=α*d₁+β*d₂+(1- α- β)*d₃). m, відповідне чистому рішенню d₁: m=1*d₁+0*d₂+0*d₃.)

Стосовно рандомізованих рішень важливим є твердження, що рандомізовані рішення не можуть зменшити мінімальний ризик, який було знайдено на чистих рішеннях.

Згідно з формулою (1), ризик рандомізованого рішення – це середньозважений ризик, розрахований з функцій втрат чистих рішень. З цього випливає, що, якщо існує ризик ρ(P,d) змішаного рішення, то його значення дорівнює суміші ризиків ρ(P,d_i) чистих рішень d_i.

З чого випливає, що

Inf_dєM [ρ(P,d)] = inf _dєD [ρ(P,d)] =ρ^*(P).

Тобто якщо є відрізок, то мініум його лежить на кінцях, і ніяк не можу бути на середині. Тобто, фактично, рандомізовані рішення задають всі можливі комбінації чистих рішень (з 2-х рішень роблять відрізок, з більше – якусь фігуру, а ця площина, що утворюється (гіперплощина у вищих просторах) не може виходити за межі твірних точок, якими і є чисті рішення.

15. Доцільність спостережень у стохастичній системі рішень. Плата за спостереження.

Загальним ризиком від спостереження X і прийняття вирішальної функції називається сума ризику й середньої ціни спостереження . Статистик повинен вибрати спостереження X з деякого класу доступних спостереженню випадкових величин і відповідну байєсівскую вирішальну функцію , яка мінімізує загальний ризик. Виражаючи загальний ризик у вигляді суми ризику вирішальної функції й середньої ціни спостереження, ми неявно використаємо припущення про аддитивності корисностей статистика.

Розглянемо приклад. Припустимо тепер, що ціна спостереження випадкової величини X дорівнює , . Статистик може або прийняти рішення, не спостерігаючи X, або заплатити суму й спостерігати X перед ухваленням рішення. При заданому апріорному розподілі запитується, на яку суму с варто погоджуватися статистику?

Для рішення цього завдання треба порівняти мінімальне значення ризику без обліку ціни спостереження с, що може бути отримане на основі спостереження X, з мінімальним ризиком , що відповідає байєсівскому рішенню при відсутності спостережень. Функція вже знайдена. Функція має вигляд

(2)

Графіки функцій і зображені на мал. 8.7. Із цього малюнка видно, що , якщо або . Отже, при значенні апріорної ймовірності , що лежить в одному із цих інтервалів, статистик може досягти й без спостереження X того ж значення ризику, що й при спостереженні X

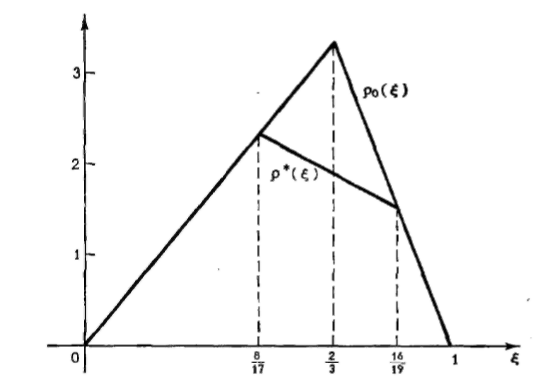
Рис. 8.7. Ризики та із приклада 1.

Якщо ж , то за можливість спостереження величини X перед ухваленням рішення статистику треба погоджуватися на будь-яку ціну , таку, що , Різницю між ризиками максимальна для , де вона дорівнює .

У багатьох статистичних задачах рішення спостереження випадкової величини X пов'язане з певними витратами, які повинні враховуватися статистиком при розрахунку ризику від прийняття вирішальної функції, що використає результати спостереження X. Ця обставина грає особливо важливу роль у випадку, коли статистику треба вирішити, яку з декількох випадкових величин краще спостерігати, або вирішити, чи робити спостереження взагалі. Нехай позначає ціну спостереження значення х величини X, якщо . Тоді, якщо є о. в. п. випадкової величини W, то середня ціна спостереження дорівнює