4. Теорема існування невизначеності у системі рішення.

Невизначеність у ЛСПР існує, якщо:

- Дві різні дії призводять до таких самих двох різних наслідків

- Якщо одна дія призводить до двох деяких наслідків, а інша до хоча б одного наслідку, відмінного від попередніх.

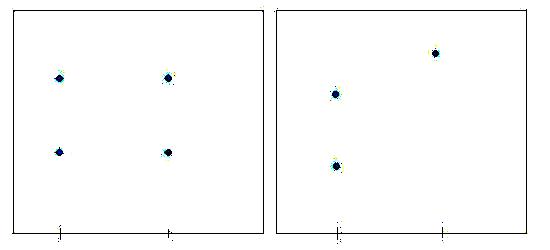
Це справедливо, якщо ми не фіксуємо Відношення Переваг на Наслідках для ТПР.

В разі, якщо існує порядок на наслідках, необхідною і достатньою умовою невизначеності буде:

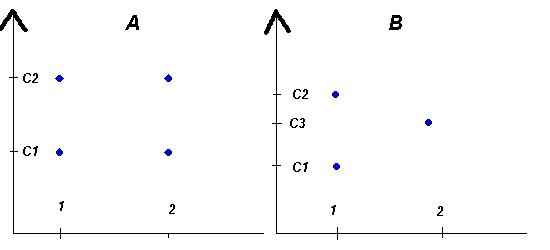
• За означенням невизначенності: "Коли два ТПР, з однаковими відношеннями переваг оберуть дві різні дії"

• У варіанті B Перший ТПР обере дію 1, бо може отримати максимальний виграш - С2, а Другий ТПР обере дію 2, бо не схильний до ризику і надає перевагу гарантованому виграшу С3

• У варіанті А, на перший погляд, дві дії еквівалентні, оскільки мають однакові наслідки. АЛЕ: завжди будуть ТПР1 та ТПР2, для яких виграш(1)>виграш(2) та виграш(1)<виграш(2) відповідно. І той та інший буде мати рацію.

Алгоритм Перевірки на невизначенність:

1)шукаємо дію (for по всіх таких діях), в якої>1 наслідку.

2) якшо 2 наслідки: шукаємо іншу дію (<> наша знайдена).

2а) якшо в неї є два наслідки, які такі ж як і наші два насліки, то ситуація невизначена.

2б) якшо в неї є наслідок, якого немає серед наших наслідків, то ситуація невизначена.

3) якшо >2 наслідків:

3а) шукаємо іншу дію (не наш знайдений) в якго є ХОЧ ОДИН наслідок. якшо знаходимо -- є невизначеність.

4. Прийняття рішення при повній невизначеності. Чотири критерії.

Критерій Вальда

матриця гри містить наші виграші.

Згідно з цим критерієм, гра з природою ведеться як гра з розумним, причому агресивним супротивником, що робить усе для того, щоб завадити нам досягти успіху. Оптимальною вважається стратегія, за якої гарантується виграш у будь-якому разі не менший, ніж "нижня ціна гри з природою", тобто стратегія із найбільшим гарантованим виграшем:

Якщо керуватися цим критерієм, що уособлює позицію "крайнього песимізму", потрібно завжди орієнтуватися на найгірші умови, знаючи наперед, що "гіршого за це не буде". Очевидно, такий підхід - "перестрахувальний", природній для того, хто дуже боїться програти, - не є єдино можливим, але як крайній випадок він заслуговує на розгляд.

Розглянемо приклад застосування критерію Вальда (мінімуми по j записані в останньому стовпчику):

	Π1	Π2	Π3	Π4	minj
A1	1	5	3	2	1
A2	2	4	3	5	2
A3	3	6	1	2	1
A4	5	3	3	4	3

Червоним виділено максимум із мінімумів по стовпчиках. Отже, критерій Вальда радить нам обрати рішення A₄, оскільки за цієї стратегії ми гарантовано виграємо не менше, ніж за будь-якої іншої.

----------------------------------------------------------------------------------------------------------

Критерий Вальда (критерий осторожного наблюдателя). Этот критерий оптимизирует полезность в предположении, что природа (внешняя среда) находится в самом невыгодном для наблюдателя состоянии. По данному критерию правило принятия решений имеет следующий вид:

 где                             (1.3.12)

По критерию Вальда выбирают стратегию, которая дает гарантированный выигрыш при наихудшем варианте состояния природы.

Критерій Севіджа

Критерій мінімаксного ризику Севіджа. Цей критерій теж крайньо песимістичний, але при виборі оптимальної стратегії радить орієнтуватись не на виграш, а на ризик прогашу, або "жаль". Обирається в якості оптимальної та стратегія, за якої величина гарантованого жалю мінімальна:

Для того, щоб застосувати критерій Севіджа, нам треба побудувати "матрицю жалів", елементи якої є різницею між максимальним виграшем за даної стратегії природи П та фактичним виграшем за нашої даної стратегії A:

Суть такого підходу в тому, щоб уникати великого ризику при прийнятті рішення. У сенсі "песимізму" критерій Севіджа схожий на критерій Вальда, але сам "песимізм" тут має інший зміст.

Розглянемо приклад. Нехай матрицю А задано наступним чином:

	Π1	Π2	Π3	Π4
A1	1	5	3	2
A2	2	4	3	5
A3	3	6	1	2
A4	5	3	3	4

Побудуємо матрицю жалів (максимуми по j записані в останньому стовпчику):

	Π1	Π2	Π3	Π4	maxj
A1	4	1	0	3	4
A2	3	2	0	0	3
A3	2	0	2	3	3
A4	0	3	0	1	3

Червоним виділено рішення A₁ , A₂, A₃, отже, згідно з критерієм Севіджа, слід обрати будь-яке з них.

Критерий Сэвиджа (критерий минимизации сожалений). Сожаление – это величина,  равная изменению полезности решения (результата) при данном текущем состоянии среды относительно наилучшего возможного состояния (для данного решения). Чтобы определить сожаление, выполняют следующие процедуры.

Вычисляют матрицу , где  . В каждом столбце этой матрицы находят максимальный элемент: Его вычитают от всех элементов столбца. Затем строят матрицу сожалений: , где . Правило выбора оптимальной стратегии в соответствии с критерием Сэвиджа записывается так:

Критерій Гурвіца

Критерій оптимізму-песимізму Гурвіца.

Цей критерій рекомендує при виборі рішення не керуватися ні крайнім песимізмом ("завжди розраховуй на найгірше"), ні крайнім, легковажним оптимізмом ("ми ж у сорочці народилися"). Згідно з цим критерієм, стратегія обирається з умови:

де χ - "коефіцієнт песимізму", що обирається між нулем і одиницею. При χ = 1 критерій Гурвіца перетворюється на критерій Вальда; при χ = 0 - на критерій "крайнього оптимізму", що рекомендує обрати ту стратегію, за якої найбільший виграш у рядку є максимальним. При 0 < χ < 1 виходить щось середнє між першим і другим. Коефіцієнт χ обирається з суб'єктивних міркувань - чим небезпечніше ситуація, чим більше ми хочемо в ній "підстрахуватися", чим менша наша схильність до ризику, тим ближче до одиниці обирається χ.

Розглянемо приклад застосування критерію Гурвіца з коефіцієнтом песимізму χ = 0,6. Нехай матрицю А задано наступним чином (мінімуми по j записано у п'ятому стовпчику, максимуми по j - в шостому):

	Π1	Π2	Π3	Π4	minj	maxj	hi
A1	1	5	3	2	1	5	2,6
A2	2	4	3	5	2	5	3,2
A3	3	6	1	2	1	6	3
A4	5	3	3	4	3	5	3.8

Червоним виділено максимум з останнього стовпчику. Критерій Гурвіца радить нам обрати рішення A₄.

Критерий Гурвица основан на следующих двух предположениях: природа может находиться в самом невыгодном состоянии с вероятностью  и в самом выгодном – с вероятностью , где  – коэффициент доверия.

Тогда правило принятия решений записывается так:

Если , то получим критерий Вальда. Если , то имеем правило вида , – которое имеет название стратегии оптимиста, который верит в свою удачу.

Критерій Лапласа

Цей критерій ще називається "принципом недостатнього обґрунтування", і, згідно з ним, припускається, що всі стани природи рівноймовірні. У такому разі обирати слід таку стратегію:

Розглянемо приклад застосування цього критерію на такій матриці (в останньому стовпчику - середнє арифметичне виграшів за даної стратегії A):

	Π1	Π2	Π3	Π4	avgi
A1	1	5	3	2	2,75
A2	2	4	3	5	3,5
A3	3	6	1	2	3
A4	5	3	3	4	3.75

Червоним виділено максимум з останнього стовпчика, отже, згідно з критерієм Лапласа, ми маємо обрати рішення A₄.

Критерий Лапласа. Если состояния природы (среды) неизвестны, то все они считаются равновероятными:

В результате правило принятия решений определяется соотношением (1.3.11).