4. Еквівалентність матричної та лотерейної моделей стохастичної ситуації (перенесення даних про невідоме).

Побудувати модель МСПР по заданій моделі (зі стохастичною закономірністю) ЛСПР

Перевести МОДЕЛЬ=перевести СХЕМУ+перевести ІНФОРМАЦІЮ. Схему переводимо аналогічно до Матрична ситуація прийняття рішень. Розподіл на W будуємо так: для кожного параметру ймовірність його появи визначатимемо, як добуток ймовірностей настання відповідних наслідків за кожної дії P(ω)=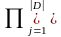 P_dj(g(ω,d_j))

Побудувати модель ЛСПР по заданій моделі (зі стохастичною закономірністю) МСПР

Z_М Z_Л - так як і в Лотерейна ситуація прийняття рішень

I_М I_Л: P_dj(c_i)= P(ω_k)

d_j D, c_i C, j 1..|D|, i=1..|C|

4. Експерименти у системі рішення та їх математичні моделі. Приклади.

Два типи спостережень (експериментів) у задачах прийняття рішень (ЗПР).

Існує два типи спостережень у ЗПР :

1. Експеремент проводиться перед тим як прийняти рішення. Досліджуються параметри середовища(параметри що впливають на дії).

y = Function(θ,Ω)

y - результат експеременту для певного параметра. . Де Ω - множина параметрів. ξ - похибка приладу. Сприймайте функцію Function як функцію-експеремент.

2. Експеремент проводиться після приняття рішення. Досліджуються наслідки минулого рішення.

y = Function(c,Ω)

- наслідок з множини наслідків.

У другому типі експеременту наявна дінаміка, тому що поточне рішення приймається спираючись на результат минулого. Тобто дінамічно.

4. Той хто приймає рішення та його математична модель. Класи тпр.

1)Будуємо відношення переваг на наслідках - всі можливі відношення переваг на множині - всі відношення переваг на , про які має уявлення ТПР - обране ТПР'ом відношення переваг

2)Знаходження оптимальног наслідку

3)Побудова відношення переваг на діях: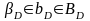

4)Оптимізація найкращого : найкраща дія

• - людина-проектор, Э П_i - класи людей

• - модель ТПР

 У загальному випадку завдання ТПР будується наступним чином: встановлюється  1. Всі можливі способи дії - альтернативи  2. Їх послідовність і числова оцінка  3. Цілі учасників процесу прийняття рішень  4. Природа впливу на цей процес різних випадкових і детермінованих керуючих факторів.  Потім підбирається відповідна модель і метод розв'язання задачі. На сьогоднішній день теорія досягла стану, коли розроблені моделі для опису практично всіх задач прийняття рішень. У рамках сучасної ТПР розроблені моделі для опису практично всіх типів задач прийняття рішень, кожному з яких відповідають певні аналітичні методи. Існує досить багато класифікацій задач теорії прийняття рішень: з урахуванням часу: статичні і динамічні, по кількості цілей дослідження: один або кілька, за кількістю критеріїв: один або декілька, за структурою учасників: з одним учасником, двома, кінцевим числом і нескінченним, за характеру вихідних даних: детерміновані та стохастичні і т.д. Кожному класу задач відповідають методи ТПР: лінійне і нелінійне програмування, критеріальні аналіз, теорія ігор і варіаційних рядів. Всі ці класифікації вірні, але охоплюють нерівноцінні області проблем, багато з дисциплін перекривають один одного з постановки завдань і методів розв'язання.  МОДЕЛІ ПРИЙНЯТТЯ РІШЕНЬ :Детерміністичних,Стохастичні ,критеріальні аналіз,теорія ігор,лінійне і нелінійне програмування ,статистичні,стратегічні, нестратегічні методи . ОПР - особа яка приймає рішення.

1)Ціль (мета) формулюється в явному або не в явному вигляді.

2)ОПР повинна мати засоби впливу для прийняття рішень.

В ролі засобів, які впливають на результат можуть виступати якісь програми, дії. Спрощено можна вважати що прийняття рішень являє собою вибір якогось варіанту із існуючого.

Задача прийняття рішень(ЗПР) - це така задача , яка може бути сформульована в термінах цілі, засоби, результати.

Математична модель ЗПР являє собою формальний опис елементів які її складають (цілі, засоби, результати), а також зв’язки між засобами і результатами. Треба звернути увагу, що в математичній моделі ЗПР повинен повністю описуватись весь набір засобів(явно/неявно).

Класифікація ЗПР здійснюється в двох аспектах:

1) Класифікація по опису засобів, результатів та зв’язків між ними.

2) Класифікація по опису цілі ЗПР.

Визначимо три множини:

1. X - множина альтернатив, тобто засобів, що ми вибираємо.

2. S - множина станів зовнішнього середовища, яка характеризує прояв невизначеності в

процесі прийняття рішення.

3. Z - множина наслідків, результат розв’язку ЗПР.

Відображення X × S → Z - відображає зв’язок між засобами і рішеннями .

Основні класи задач.

1)Найпростіший тип зв’язку - детермінований , коли кожна альтернатива приводить до одного наслідку. В цьому випадку існує функціональна залежність між альтернативою x і наслідком z . Такі ЗПР називаються детермінованими.

2)Не детермінований тип, тобто кожній альтернативі відповідає не один і той самий наслідок. Якщо відомо з якою ймовірністю кожній альтернативі буде відповідати наслідок , тоді маємо статистичну заленість між x й z . В цьому випадку ЗПР називається задачею в умовах ризику або стохастичної невизначеності.

3)ЗПР проходить в умовах невизначеності, тобто відображення між множинами X та Z неоднозначне, але статистична залежність відсутня. Тут існують два випадки:

- якщо S поводить себе пасивно до ОПР(є проявом стихії, природи), то маємо ЗПР в невизначених умовах.

- якщо S поводить себе активно до ОПР, тобто приймає участь інша особа, тварина і т.д. ЗПР в умовах конфлікту (гри).

4)Якщо хоч одна з множин є нечіткою, чи нечітким є відображення X × S → Z тоді кажуть, що ПР проходить в умовах нечіткої інформації .