3.7.5. Алгоритм та числовий приклад розв'язування прямої та оберненої геодезичних задач на поверхні еліпсоїда на основі чисельного методу (формул Рунге-Кутта) а) алгоритм

Алгоритм розв'язування приведений для випадку, коли можна виконати інтегрування зразу по всій довжині геодезичної лінії (до 100 км) без поділу її на частини, тобто h=s.

Пряма геодезична задача

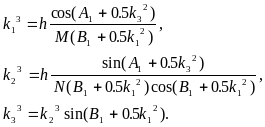
Обернена геодезична задача

• алгоритм оберненої геодезичної задачі на поверхні сфери:

• за величинами B₁,L₁, S’, A₁’ розв’язують пряму геодезичну задачу на поверхні еліпсоїда (див. її алгоритм) і знаходять B₂’,L₂’,A₂’;

• за різницями координат B=B₂-B₂’,

L=L₂ - L₂’ з допомогою диференційних формул

уточнюють значення довжини лінії та азимута

• з новими значеннями та знову переходять до розв'язування прямої геодезичної задачі і дальше за алгоритмом. Критерієм закінчення обчислень служить умова:

• в разі виконання поставленої умови отримують остаточні значення A₁, A₂, s.

Б) числовий приклад

Для еліпсоїда Красовського:

Вихідні дані:

Пряма геодезична задача

Позначення	Числові значення
k11 k21 k31 k12 k22 k32 k13 k23 k33 k14 k24 k34 B2 L2 A2	0.00665714 0.01032792 0.00791165 0.00663054 0.01040993 0.00799670 0.00663025 0.01041021 0.00799682 0.00660326 0.01049310 0.00808272 50o22’47.60412” 24o35’47.26145” 225o27’29.480”

Обернена геодезична задача

Обернена геодезична задача на сфері
s’ A1’		60202.28 44o55’15”
Пряма геодезична задача на еліпсоїді			Диференційні формули
B2’ L2’ A2’	50o22’54.1097” 24o35’51.6089” -		dS dA	-202.321 284.29”
			s=s’+dS A1=A1’+dA	59999.958 44o59’59.823”
B2’ L2’ A2’	50o22’47.6044” 24o35’47.2581” -		dS dA	0.041 0.1768”
			s=s’+dS A1=A1’+dA	59999.999 45o00’00”
B2’ L2’ A2’	50o22’47.6041” 24o35’47.2614” 225o27’29.479”		dS dA	0 0
			s=s’+dS A1=A1’+dA	59999.999 45o00’00”
A1 A2 s			45o00’00” 225o27’29.479” 59999.999 м

3.7.6. Алгоритм та числовий приклад розв'язування прямої та оберненої геодезичних задач в просторі. А) алгоритм Пряма геодезична задача

• 

• 

• 

• 

• 

• 

• 

• 

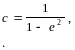
Обернена геодезична задача

• 

• 

• 

• 

• 

б) числовий приклад

Для еліпсоїда Красовського:

Вихідні дані: