Розділ 3. Розв'язування геодезичних задач

3.6. Способи розв’язування головних геодезичних задач на поверхні еліпсоїда.

3.6.1. Розв’язування головних геодезичних задач методом із середніми аргументами (формули Гаусса). Пряма геодезична задача

Нехай на рис.3.7 крива Q₁Q₂ є геодезичною лінією між початковою точкою Q₁ і кінцевою Q₂.

Рис.3.7

Візьмемо точку Q_o, розташовану на середині геодезичної лінії Q₁Q₂. Застосувавши формули (3.32) до кожної частини геодезичної лінії, отримаємо для широти

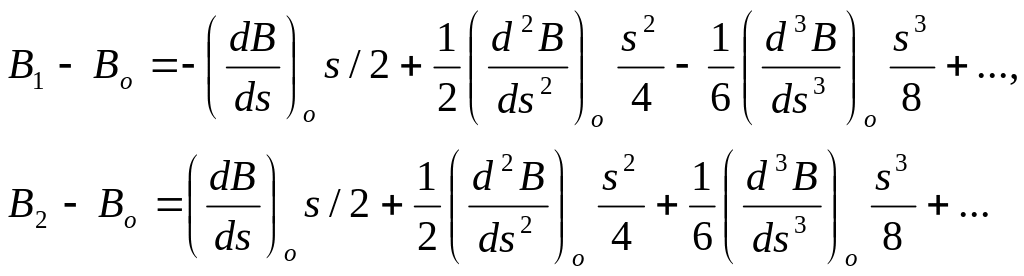(3.56)

Віднявши в (3.56) перше рівняння від другого знаходимо

Для різниць довгот та азимутів отримаємо аналогічно:

д е нульовий індекс при похідних показує, що вони повинні обчислюватись за B_o і A_o. Отримані вирази мають перевагу перед формулами (3.32): члени з парними степенями відсутні, а в інших членах коефіцієнти при них зменшились в декілька раз. Проте координати точки Q_o(B_o, L_o, A_o), яка розташована посередині геодезичної лінії Q₁Q₂, не будуть рівні середньому значенню координат цих точок (B_m, L_m,, A_m).

Залежності між цими координатами можна отримати, якщо додати рівняння (3.56) і поділити на два:

(3.57)

Аналогічно

.

.

Як видно, ці залежності – малі величини другого порядку.

Приведені вище формули в загальному виді розв’язують поставлену задачу. Але поскільки ставиться за мету отримати різниці координат у функції B_m і A_m, то потрібно встановити залежність між вказаними похідними. Вона виражається з допомогою ряда Тейлора:

.

Часткові похідні, що входять в дану формулу дорівнюють:

З похибкою на малі величини четвертого порядку, остаточно отримаємо

(3.58)

а з похибкою на величину третього порядку можна записати:

(3.59)

Використавши вирази (3.59) для перетворення поправочних членів у формулі (3.58) і не приймаючи до уваги члени і менше, отримаємо для різниці широт остаточно:

(3.60)

Для різниці довгот та азимутів формули отримуються аналогічним чином. Запишемо ці формули в кінцевому виді

(3.61)

(3.62)

Наведені скорочені формули для різниць широт, довгот та азимутів відрізняються від повних формул типу (3.58), які точні до величин четвертого порядку включно, лише на відкинуті малі величини порядку .

В формулах (3.60)-(3.62) величини b,l,a – функції середньої широти B_m і середнього азимута A_m, які невідомі. Невідомі також і аргументи b і l в поправочних членах вказаних формул. Тому пряма геодезична задача розвязується методом послідовних наближень наступним чином.

Приймаємо b і a рівними нулю, тобто

і з цими значеннями обчислюємо в першому наближенні b^І ,l^І ,a^І, а потім знаходимо

(3.63)

З цими наближеними значеннями знаходимо нові, більш точні значення B_m і A_m та повторюємо обчислення b і a, а також l. Так поступають до тих пір, поки результати обчислень із двох суміжних наближень не стануть одинаковими.

Обернена геодезична задача.

При відомих значеннях ми можемо зразу знайти

Для знаходження невідомих використовують отримані вище формули для прямої геодезичної задачі. При цьому для обчислення достатньо знайти та . Тоді отримаємо

Для знаходження A_m представимо формули (3.60) та (3.61) у виді

(3.64)

_{Розділивши ці два рівняння, отримаємо}

(3.65)

Величину знаходимо на основі формули (3.62)

(3.66)

Довжину геодезичної лінії легко знаходимо із рівнянь (3.64)

(3.67)