2. Метод взвешенной суммы оценок частных критериев.

При таком подходе формулируется скалярный критерий как взвешенная сумма оценок частных критериев:

где — вес, задаваемый экспертами или непосредственно ЛПР, с учетом особенностей задачи. При этом точка минимума принимается в качестве наилучшего решения.

g1 (2)-вес g2 (2)-вес g3 (1)-вес F(x) A 10 8 40 76 B 12 6 40 76 C 8 11 40 78 D 9 10 45 83 E 10 8 41 77

3. Минимаксный обобщённый критерий

При таком подходе на основе частных критериев исходной многокритериальной задачи формируется обобщенный критерий следующим образом:

где — коэффициент важности каждого критерия (достаточно часто на практике в качестве коэффициента выбирают значение ). Точки минимума этой критериальной функции принимаются как искомые оптимальные решения.

g1 g2 g3 Макс сg A 10 8 40 40 B 12 6 40 40 C 8 11 40 40 D 9 10 45 45 E 10 8 41 41

4. Минимизация обобщённого скалярного критерия

При таком подходе к решению исходной многокритериальной задачи минимизации формируется скалярный обобщенный критерий следующим образом

где — минимальное значение каждого частного критерия на допустимой области X. Точки минимума этой критериальной функции принимаются как искомые оптимальные решения из множества эффективных решений, оптимальных по Парето.

5. Обобщенные критерии

Направление на утопическую точку ,

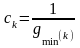
g1 5 g2 7 g3 1 A 10 8 40 160/3 B 12 6 40 60 C 8 11 40 77 D 9 10 45 67 E 10 8 41 160/3- не парето УТ 8 6 40

6. Метод последовательных уступок

Если частные критерии могут быть упорядочены в порядке убывающей важности. А именно, пусть — наиболее важный, — наименее важный среди всех N рассматриваемых частных критериев..

1) решается однокритериальная задача для первого наиболее важного критерия:

при условии .

По завершению первого этапа исходя из практических соображений и принятой точности назначается некоторая уступка ∆₁ > 0, которую можно допустить в рамках реализации этого метода с, чтобы перейти ко второму этапу — минимизации следующего критерия. При этом , что реализуется в качестве соответствующего ограничения на следующем этапе метода.

2)

И т.д аналогично. На последнем шаге:

g1 g2 g3 A 10 8 40 B 12 6 40 C 8 11 40 D 9 10 45 E 10 8 41

7. Метод идеальной точки

Состоит в нахождении точки, дающей решение, ближайшее к так называемой утопической точке, которую, обычно, задает ЛПР.

	g1	g2	g3
A	10	8	40
B	12	6	40
C	8	11	40
D	9	10	45
E	10	8	41
УТ	8	6	40

1

*

85