Заключение

В данном уроке вы изучили как выводить 3d геометрию на экран и познакомились с шейдерами, которые нужны для её отображения. В следующем уроке мы познакомимся уустановкой камеры, но сначала мы немного погрузимся в обширный мир 3d математики, и вплотную столкнемся с матрицами.

Урок 3. Математические основы Direct3d

Прежде чем приступать к дальнейшему изучению DirectX необходимо ознакомится с тем, какими данными мы будем в дальнейшем оперировать. Конечно, вы уже знаете что одна вершина модели характеризуется тремся координатами XYZ, однако для того чтобы работать в DirectX этого недостаточно.

Знакомство с базовыми 3d представлениями данных

Расстояние от начала координатной системы и положение точки в пространстве называется координатой.

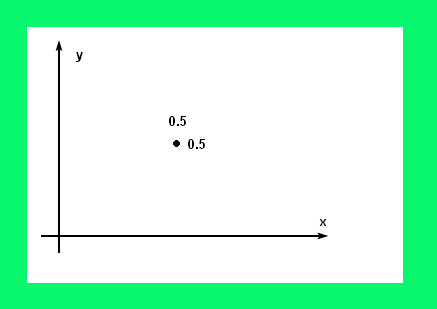
Отрезок произвольной длинны, называется вектором. Вектор может быть представлен двумя способами:

• Заданием компонент вектора.

• Заданием направления и модуля вектора.

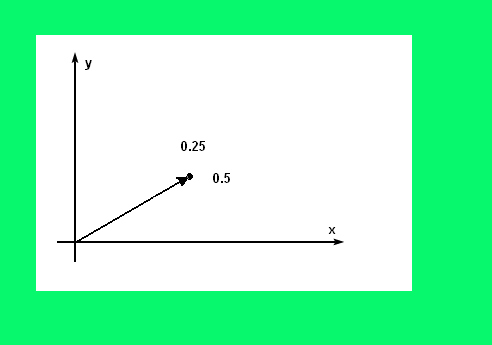
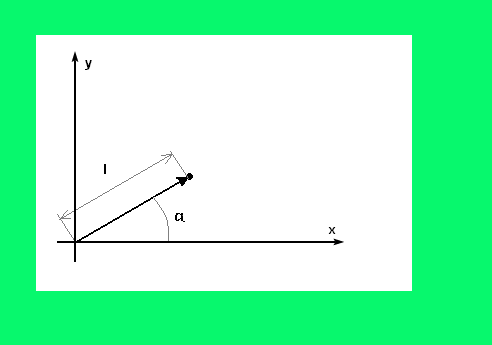
Компонентами вектора A называются длины проекций этого вектора на каждую из осей координат.

Если вкратце, то компоненты вектора – это просто координаты конечной точки вектора. Задание трехмерного вектора в виде компонент математически выглядит как:

Модулем вектора A называется длинна вектора, она равна по абсолютной величине квадратному корню из суммы квадратов компонент вектора. Любой вектор характеризуется направлением, которое задается одним или более углов между выбранными осями координат (ортами) и модулем этого вектора.

Теперь рассмотрим третий ключевое понятие DirectX – Матрицы. Матрицей называется объект, состоящий из наборов чисел, сгруппированных в столбцы и строки. В основном в DirectX используются четырехрядные матрицы:

Преобразования векторов и операции с ними

Вектора, можно рассматривать как обычные числа, ведь одной переменной можно присвоить целый вектор:

Математические операции с векторами

Так как теперь вектор является своего рода числом, то с ним можно осуществлять различные математические опреции, а именно:

• Сложение векторов

• Вычитание векторов

• Умножение векторов

• Деление вектора на число

Математически это выглядит следующим образом:

Модуль вектора

Модулем вектора называется длинна вектора, она равна по абсолютной величине квадратному корню из суммы квадратов компонент вектора.

Скалярное и векторное умножении векторов

Умножение векторов отличается от умножения обычных чисел. Во первых, существует два вида умножения векторов: скалярное и векторное.

Результатом скалярного умножения векторов является число, равное косинусу угла между векторами (этот угол определен в плоскости, на которой лежат эти вектора) умноженному на произведение модулей этих векторов:

Результатом векторного умножения вектокторов является вектор,

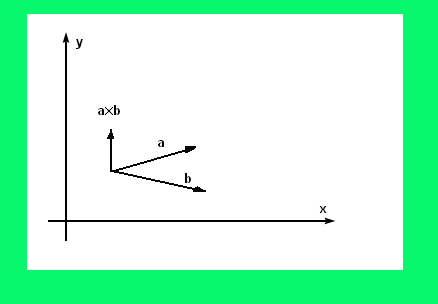
перпедникулярныйобеим исходным векторам, то есть перпендикулярной плоскости, в которой лежат эти вектора, этот вектор по модулю равен синусу угла между  векторами умноженному на произведение модулей этих векторов.

Норма вектора

Нормой вектора называется модуль вектора.