Максиминный критерий Вальда.

Согласно этому критерию в качестве оптимальной выбирается та стратегия игрока А, при которой минимальный выигрыш максимален, т. е. стратегия гарантирующая при любых условиях выигрыш не меньше,чем максимин:

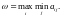(6.19)

Если руководствоваться этим критерием, нода всегда ориентироваться на худшие условия и выбирать ту стратегию, для которой в худших условиях выигрыш максимален. Пользуясь таким критерием в играх с природой, мы как бы ставим взамен нее активного и злонамеренного противника. Критерий крайнего пессимизма.

Критерий минимаксного риска Сэвиджа.

Этот критерий рекомендует в условиях неопределенности выбирать ту стратегию, при которой величина риска принимает наименьшее значение в самой неблагоприятной ситуации (когда риск максимален):

(6.20)

Сущность этого критерия в том, чтобы любыми путями избежать большого риска пи принятии решения.

Как и критерий Вальда это критерий крайнего пессимизма, но только пессимизм здесь понимается не как минимальный выигрыш, а как максимальная потеря выигрыша по сравнению с тем, чего можно было бы достичь в данных условиях (максимальный риск).

Критерий пессимизма-оптимизма Гурвица.

Критерий Гурвица имеет вид:

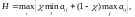(6.21)

где — коэффициент от 0 до 1.

При критерий Гурвица превращается в пессимистический критерий Вальда; при 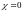— в критерий ‘‘крайнего оптимизма’’ (в наилучших условиях максимальный выигрыш).

При 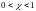получается нечто среднее между крайним пессимизмом и крайним оптимизмом. — ‘‘мера пессимизма’’ исследователя (чем опаснее ситуация, тем ближе к 1).

Пример 3. Рассматривается игра с природой 4´3 с четырьмя стратегиями игрока А₁, А₂, А₃, А₄ и тремя вариантами условий (состояний природы) П₁, П₂, П₃. Матрица выигрышей задана таблицей

aij	П1 П2 П3
A1 A2 A*3 A4	0.2 0.3 0.15 0.75 0.2 0.35 0.25 0.8 0.25 0.85 0.05 0.45

Найти оптимальное решение (стратегию), пользуясь критериями Вальда, Сэвиджа и критерием Гурвица при c=0.6.

Решение:

1. Критерий Вальда.

В каждой строке матрицы берем наименьший выигрыш:

aij	П1 П2 П3	ai
A1 A2 A3 A4	0.2 0.3 0.15 0.75 0.2 0.35 0.25 0.8 0.25 0.85 0.05 0.45	0.15 0.2 0.25* 0.05

Из величин a_i максимальная равна 0.25, следовательно, по критерию Вальда оптимальной является стратегия A₃.

2. Критерий Сэвиджа.

Стоим матрицу рисков и помещаем в правом добавочном столбце максимальный риск в каждой строке g_i:

rij	П1 П2 П3	gi
A1 A*2 A*3 A4	0.65 0.5 0.3 0.1 0.6 0.1 0.6 0 0.2 0 0.75 0	0.65 0.6* 0.6* 0.75

Максимальным из значений g_i является 0.6, следовательно, по критерию Сэвиджа оптимальной является любая из стратегий A₂, A₃.

3. Критерий Гурвица (c=0.6).

Записываем в правых трех столбцах матрицы “пессимистическую” оценку выигрыша a_i, “оптимистическую” w_i и их среднее взвешенное по формуле (6.21):

h_i=0.6a_i + 0.4w_i.

aij	П1 П2 П3	ai	wi	hi
A1 A2 A3 A4	0.2 0.3 0.15 0.75 0.2 0.35 0.25 0.8 0.25 0.85 0.05 0.45	0.15 0.2 0.25 0.05	0.3 0.75 0.8 0.85	0.21 0.42 0.47* 0.37

Максимальное значение h_i соответствует стратегии A₃. Следовательно по критерию Гурвица с легким перевесом в сторону пессимизма (c=0.6) оптимальной стратегией является A₃, которую мы имеем все основания выбрать.

Анализ матрицы игры с природой под угол зрения разных критериев часто дает лучшее представление о ситуации, о достоинствах и недостатках каждого решения, чем непосредственное рассмотрение матрицы, особенно, когда ее размеры велики.

Аналогичным образом каждый из критериев может быть сформулирован для смешанных стратегий. Решение будет найдено как решение задачи линейного программирования.

Основное содержание теории статистических решений — это планирование получения и использования дополнительной информации о состояниях природы, которую можно добыть путем эксперимента. Исследования показывают, что в типичных случаях, когда речь идет о получении сколько-нибудь значительного количества дополнительной информации, критерии, не пользующиеся вероятностями состояний (Вальда и другие), становятся практически равносильными критерию, основанному на вероятностях состояний. А для последних, мы знаем, использование смешанных стратегий не имеет смысла. Т. е., если мы можем получить сколько-нибудь дополнительной информации, применение смешанных стратегий теряет смысл (каким бы из критериев выбора решения мы не пользовались).