Оптимальной стратегией игрока А является чистая стратегия А₂, хотя это и не соответствует точке пересечения стратегий. Здесь стратегия А₂ игрока А явно (при любой стратегии противника) выгоднее стратегии А₁.

I II

B₂

B₁ B₂

a₁₂ B₁

a₁₁ = n a₂₂

a₂₁

0 1 x

S_A^*=A₁ p₁

Рис.6.4.

На Рис.6.4 изображен случай, когда заведомо невыгодная стратегия имеется у противника (игрока В).

I II

B₂ B₁

N

K L

B₂

n b

B₁ a

0 1 x

p₂ S_A^* p₁

Рис.6.5.

На Рис.6.5 геометрическая интерпретация дает возможность наглядно изобразить также нижнюю цену a и верхнюю b. На том же графике можно дать и геометрическую интерпретацию оптимальных стратегий противника В. Действительно, можно убедиться, что доля q₁ стратегии В₁ в оптимальной смешанной стратегии S_B^*=(q₁, q₂) равна отношению длины отрезка КВ₂ к сумме длин отрезков КВ₂+КВ₁ на оси I: q₁=КВ₂/(КВ₂+КВ₁), или, что то же, q₁=LB₂/(LB₂+LB₁) на оси II.

Оптимальную стратегию S_B^*=(q₁, q₂) можно найти и непосредственно, поменяв местами игроков А и В, и вместо максимальной нижней границы выигрыша рассматривать минимум верхней границы:

I II

A₂ A₁

N

A₁

a₂₂ n a₁₂

a₁₁ A₂

a₂₂

0 1 x

q₂ S_B^* q₁

Рис.6.6.

Геометрическая интерпретация решения игры “поиск”:

I II

B₁

B₂ N

B₁

n B₂

0 1 x

p₂ S_A^* p₁

Рис.6.7.

5. Игры 2´n и m´2.

Мы убедились, что любая игра 2´2 может быть решена элементарными приемами. Совершенно аналогично может быть решена любая игра 2´n, где у нас (А) имеется две стратегии, а у противника (В) - произвольное количество n.

Итак, пусть имеется матрица игры 2´n. Зададим геометрическую интерпретацию - n стратегий противника изобразятся n прямыми:

I II

B₂

B₃ B₁

N B₃

M K

B₂

B₄

0 1 x

B₁ p₂ S_A^* p₁

Рис.6.8.

Нижняя граница выигрыша - ломаная В₁MNB₂. Точка с максимальной ординатой на ней - N. Эта ордината - цена игры n, а абсцисса точки N будет равна вероятности р₂ стратегии А₂ в оптимальной смешанной стратегии игрока А:

S_A^*=(p₁,p₂).

Зная, какие стратегии пересекаются в точке N, можно указать активные стратегии противника: в данном случае оптимальная смешанная стратегия

S_B^*=(0,q₂,0,q₄)

состоит из смеси двух активных стратегий В₂ и В₄. Стратегия В₃ является заведомо невыгодной, а стратегия В₁ - невыгодна при оптимальной стратегии S_A^*. Вероятности q₂ и q₄ относятся как длины отрезков КВ₄ и КВ₂.

Если А будет пользоваться своей оптимальной стратегией S_A^*, то выигрыш не изменится, какой бы из своих активных стратегий ни пользовался В; однако он изменится, если В перейдет к стратегии В₁ или В₃.

У любой конечной игры m´n существует решение, в котором число активных стратегий каждой стороны не превосходит наименьшего из чисел m и n.

Из этого, в частности следует, что у игры 2´n всегда имеется решение, в котором с каждой стороны участвует не более двух активных стратегий. Когда эти стратегии найдены, игра 2´n превращается в игру 2´2, решение которой выше получено.

Практическое решение игры 2´n сводится к построению геометрической интерпретации (Рис.6.8) и нахождению пары стратегий, пересекающихся в точке (N), соответствующей решению игры (если пересекаются больше двух стратегий, то берется любая пара). Эти стратегии и представляют собой активные стратегии игрока В.

Очевидно, что игра m´2 может быть решена точно так же, с той лишь разницей, что строится не нижняя, а верхняя граница выигрыша, и на ней ищется не максимум, а минимум.

6. Решение игры m´n.

В общем случае, при m>2, n>2, решение игры m´n может быть сведено к уже известной задаче линейного программирования.

Рассмотрим игру m´n игрока А (стратегии А₁,А₂,..,А_m) и игрока В (стратегии В₁,В₂,...,В_n). Задана матрица игры (а_ij) (без седловой точки).

Требуется найти решение игры, то есть две оптимальные смешанные стратегии игроков А и В

S_A^*=(p₁, p₂,...,p_m), S_B^*=(q₁,q₂,...,q_n),

где p_i, q_j - вероятности применения чистых стратегий ( , ).

Найдем сначала оптимальную стратегию S_A^*. Эта стратегия должна обеспечить нам выигрыш, не меньше n, при любом поведение противника, и выигрыш, равный n, при его оптимальном поведении (то есть при стратегии S_B^*).

Цена игры n нам пока неизвестна. Не нарушая общности, можно предположить ее равной некоторому положительному числу n>0. Для этого достаточно, чтобы все элементы матрицы (а_ij) были неотрицательными, а этого можно добиться, прибавляя ко всем элементам матрицы (а_ij) одну и ту же достаточно большую положительную величину М. При этом цена игры увеличится на М, а решение не изменится.

Предположим, что мы применяем свою оптимальную стратегию S_A^*, а противник (В) - свою чистую стратегию В_j. Тогда наш средний выигрыш будет:

a_j=p₁ a_{1 j} +p₂ a_2j+...+p_m a_{m j} (j=1,...,n).

Наша оптимальная стратегия S_A^* обладает тем свойством, что при любом поведении противника обеспечивает нам выигрыш, не меньше n. Значит, любое из чисел a_j не может быть меньше n. Получаем условие:

(6.9)

Разделим неравенства (6.9) на n>0 и введем обозначения:

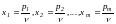(6.10)

Тогда условия (6.9) запишутся в виде:

" i x_i³0. (6.11)

Поскольку , то из (6.10) следует:

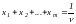. (6.12)

Мы хотим сделать свой гарантированный выигрыш максимально возможным; при этом правая часть (6.12) принимает минимальное значение. Таким образом, задача решения игры свелась к следующей математической задаче:

Определить неотрицательные значения переменных х₁, х₂,..., х_m так, чтобы они удовлетворяли линейным ограничениям (6.11) и при этом их линейная функция

L=x₁+x₂+...+x_m (6.13)

обращалась в минимум.

Это - типичная задача линейного программирования; решая ее, мы можем найти оптимальные стратегии S_A^* игрока А.

Теперь найдем оптимальную стратегию S_B^* игрока В. Все аналогично решению игры для игрока А, разница в том, что игрок В стремится не максимизировать, а минимизировать выигрыш, а значит, максимизировать величину 1/n. Вместо условий (6.11) должны выполняться условия:

"j y_j³0, (6.14)

y_j=q_j/n, j=1,...,n.

Требуется найти такие значения y_j, чтобы они удовлетворяли условиям (6.14) и обращали в максимум линейную функцию

L=y₁+y₂+...+y_n=1/n (6.15)

(либо L’=-L=-y₁-...-y_n=-1/n ® min).

Таким образом, решение любой конечной игры m´n сведено к паре задач линейного программирования.

Из особенностей задачи линейного программирования, к которой сводится решение любой конечной игры, вытекает

Основная теорема существования решения конечных игр:

Допустимое решение ЗЛП, соответствующей конечной игре m´n, всегда существует.

Доказательство:

Решение ЗЛП не существует, если

1) допустимая область пуста;

2) целевая функция не ограничена снизу (для канонического вида).

Проверим, как обстоит дело с ЗЛП, соответствующей конечной игре.

1) Сделаем элементы матрицы (а_ij) строго положительными (прибавим большое число М) и найдем наименьший элемент: .

Положим х₁=1/m , х₂=х₃=...=х_m=0 (цена игры n=m). Эта система значений переменных х₁, х₂,...,х_m представляет собой допустимое решение ЗЛП - все они неотрицательны и удовлетворяют условиям (6.11).

2) Убедимся, что линейная функция (6.13) не может быть неограниченной снизу. Действительно, все х_i неотрицательны, коэффициенты при них в (6.13) – положительны (+1), значит, функция L в формуле (6.13) тоже неотрицательна, значит, она ограничена снизу нулем, и решение ЗЛП (а, соответственно, и игры m´n) существует.

Пример. Найти решение игры “ три пальца”.

Матрица игры имеет вид:

	В1	В2	В3
А1	2	-3	4
А2	-3	4	-5
А3	4	-5	6

Прибавляя ко всем элементам матрицы число М=5, сделаем их неотрицательными:

	В1’	В2’	В3’
А1’	7	2	9
А2’	2	9	0
А3’	9	0	11

При этом цена игры увеличится на 5, а решение не изменится. Обозначим новую цену игры n’=n+5.

Найдем оптимальную смешанную стратегию игрока А S_A^*=(p₁, p₂, p₃).

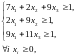
L=x₁+x₂+x_3®min

Для игрока В оптимальная смешанная стратегия S_B^*=(q₁, q₂, q₃) находится из задачи:

"j y_i³0,

L=y₁+y₂+y_{3 ®} max.

Решая сформулированную ЗЛП симплексным методом, получим оптимальную стратегию S_A^*=(1/4, 1/2, 1/4). Значение целевой функции L_min=1/5. Далее находим цену игры:

n’=1/ L_min=5 Þ n=n’-5=0.

Так как матрица (a_ij) – симметричная, то оптимальная стратегия игрока В будет такой же, как и у А:

S_В^*=(1/4, 1/2, 1/4).

В данном примере все три стратегии каждого игрока активны. Такая игра, в которой все стратегии игроков активны, называется полностью усредненной.

Если игра является полностью усредненной, т.е. все стратегии обеих сторон являются активными, неравенства (6.11) обращаются в равенства. Решив получившуюся систему уравнений, имеем положительные значения x₁, x₂,…,x_m. Отсюда цена игры:

,

а вероятности p₁, p₂,…, p_m в оптимальной стратегии S_A^*:

p_i=x_in, i=1,…,m.

Предположение о полной усредненности игры обычно делается в случае игры с квадратной матрицей (т.е. m=n). Такое решение существует по утверждению:

Для любой игры m´n существует решение, в котором с обеих сторон участвует число стратегий, равное min(m, n).

7. Элементы теории статистических решений.

В задачах теории игр, рассматривая операции, проводимые в условиях неопределенности, мы связывали эту неопределенность с неизвестным для нас поведением противника, который являлся ‘‘разумным и злонамеренным’’ и предпринимает только те действия, которые для нас наименее выгодны.

Однако, при исследовании операций приходится встречаться не только с таким видом неопределенности. Очень часто такая неопределенность связана не с сознательным противодействием противника, а с нашей недостаточной осведомленностью об условиях проведения операции. Например, могут быть заранее не известны: погода в некотором районе, покупательский спрос на определенную продукцию, объем перевозок, которые придется выполнить железной дороге, и так далее.

Все эти условия объективной действительности в теории решений принято называть ‘‘природой’’. Соответствующие ситуации часто называются ‘‘играми с природой’’. ‘‘Природа’’ в теории статистических решений рассматривается как некая незаинтересованная сторона, ‘‘поведение’’ которой не известно, но, во всяком случае, не содержит элемента сознательного противодействия нашим планам.

Рассмотрим такую ситуацию. Пусть у нас (сторона А) имеется m возможных стратегий А₁, А₂, …, А_m; относительно объективных условий можно сделать n предположений П₁, П₂,…, П_n — это ‘‘стратегии природы’’. Наш выигрыш при каждой паре стратегий А_i, П_j задан, как и раньше, матрицей игры (а_ij):

	П1	П2	. . .	Пn
A1	a11	a12	. . .	a1n
A2	a21	a22	. . .	a2n
. . .	. . .	. . .	. . .	. . .
Am	am1	am2	. . .	amn

Требуется выбрать такую стратегию игрока А (чистую или смешанную), которая является предпочтительнее (более выгодна).

В игре с природой, казалось бы, нам легче получить больший выигрыш, чем в игре с противодействующим противником; однако обоснованное решение, которое даст хороший выигрыш, здесь принять труднее. Действительно, ведь рассуждения о ‘‘наихудшем’’ для нас поведении противника снимает неопределенность в выборе. Если такого предположения нет, то неопределенность сказывается гораздо более сильно.

Как и в игре двух противников, матрицу игры с природой необходимо попытаться упростить. Однако надо учесть, что избавляться мы можем только от своих невыгодных стратегий, так как ‘‘природа’’ не выбирает свою стратегию ‘‘наихудшим’’ для нас образом.

Например, в следующей таблице можно отбросить стратегии А₁, А₂, заведомо невыгодные по сравнению с А₄, и стратегию А₅ – по сравнению с А₃, в результате чего матрица сведется к матрице 2´5.

	П1 П2 П3 П4 П5
A1 A2 A3 А4 А5	5 3 4 2 1 5 3 2 1 1 1 2 5 4 3 7 6 7 3 1 1 2 3 4 3

Þ

	П1 П2 П3 П4 П5
A3 А4	1 2 5 4 3 7 6 7 3 1

В дальнейшем будем предполагать, что анализ матрицы и отбрасывание заведомо не выгодных и дублирующих стратегий уже произведены.

В процессе принятия решения мы, конечно же, должны исходить из матрицы выигрышей (а_ij). Однако, иногда картина ситуации которую дает матрица выигрышей, содержит своего рода ‘‘искажения’’.

Например, выигрыш при стртегии А_i и состоянии природы П_j больше, чем при стратегии А_k и состоянии П_l :

a_ij>a_kl.

Но первый выигрыш может быть больше второго не за счет того, что мы выбрали более удачную стратегию, а за счет того, что состояние природы П_j “выгоднее” для нас, чем состояние П_l. Например, для какой – нибудь экономической операции (и не только экономической) состояние “отсутствие стихийных бедствий” вообще более благоприятно, чем состояние “наводнение”, “землетрясение” и тому подобное.

Поэтому желательно ввести такие показатели, которые не просто задавали бы выигрыш в каждой ситуации, но и описывали бы “удачность” или “неудачность” применения данной стратегии в данной ситуции, с учетом того, насколько вообще эта ситуация благоприятна для нас.

С этой целью в теории решений вводится понятие “риска”.

Риском игрока при пользовании стратегией А_i в условиях П_j называется разность между выигрышем, который он получил бы, если бы знал П_j, и выигрышем, который он подучит в тех же условиях, применяя стратегию A_i.

Обозначим r_ij риск игрока при его стратегии А_i в условиях П_j. Выразим риск r_ij через элементы матрицы выигрышей (а_ij). Очевидно, если бы игрок знал заранее состояния природы (условия) П_j, он выбрал бы ту стратегию, которой соответствует максимальный выигрыш в данном столбце — b_j. Тогда, согласно определению риска:

r_ij=b_j-a_ij, (6.16)

где

Из этого определения следует, что r_ij³0.

При вычислении риска величина b_j является уровнем благоприятности данного состояния для нас.

Матрица рисков (r_ij) дает зачастую более наглядную картину неопределенности ситуации, чем матрица выигрышей (а_ij).

Пример. Планируется операция в заранее не ясных условиях, например, касающихся рыночной конъюнктуры. Относительно этих условий можно сделать предположения П₁, П₂, П₃, П₄. Выгодность операций (ожидаемая прибыль) при наших стратегиях (A_i) для различных условий (П_j) задана матрицей выигрышей (a_ij).

	П1 П2 П3 П4
A1 A2 A3	1 4 5 9 3 8 4 3 4 6 6 2

Построить матрицу рисков (r_ij).

Решение: b₁=4, b₂=8, b₃=6, b₄=9.

Матрица рисков:

	П1 П2 П3 П4
A1 A2 A3	3 4 1 0 1 0 2 6 0 2 0 7

Сравним стратегии А₂ в условиях П₁ и в условиях П₄:

а₂₁=а₂₄=3.

В матрице же рисков соответствующие значения:

r₂₁=1 , r₂₄=6.

Если при состоянии природы П₁ и при выборе стратегии А₂ наш выигрыш всего на единицу меньше максимально возможного, и этот выбор очень хорош, то при состоянии П₄ и той же стратегии А₂ наши потери в выигрыше составят уже шесть единиц, и выбор стратегии А₂ очень плох.