Тема 3. Основы финансовой математики

В процессе оценочной деятельности при использовании доходного подхода важно располагать данными ценности (стоимости) денег во вре­мени, например:

1. Любой оцениваемый проект связан с инвестициями, при этом от момента вложения денег до момента получения результатов протекает определенное время.

2. Принимая решение об инвестировании денег в анализируемый про­ект, необходимо учитывать: инфляцию, риск и неопределенность, воз­можность альтернативного использования денег.

Таким образом, одна и та же денежная сумма имеет разную ценность во времени по отношению к текущему моменту. Для обращения к теории ценности денег введем условные обозначения:

FV — будущая ценность денег;

РV — текущая ценность денег (принципал или первоначальная цен­ность);

i — ставка процента;

t — продолжительность периода времени.

Расчет исчисления реальной ценности (стоимости) денег основан на временной оценке денежных потоков, которая основана на следующем. Цена приобретения объекта недвижимости определяется, в конечном счете, величиной дохода, который инвестор предполагает получить в будущем. Однако покупка объекта недвижимости и получение доходов происхо­дят в разные отрезки времени. Поэтому простое сопоставление величи­ны затрат и доходов в той сумме, в которой они будут отражены в фи­нансовой отчетности, невозможно (например, 10 млн. рублей готового дохода, полученные через 3 года, будут меньше этой суммы в настоящее время). Однако на стоимость денег оказывают влияние не только инфор­мационные процессы, но и основное условие инвестирования — вло­женные деньги должны приносить доход.

Приведение денежных сумм, возникающих в разное время, к сопо­ставимому виду называется временной оценкой денежных потоков. Вре­менная оценка денежных потоков основана на использовании шести функций денег (шести функций сложного процента): 3 функции основные и 3 функции, которые получают как обратные к основным функциям величины.

Основная функция	Обратная функция
1. Накопленная сумма единицы. 3. Текущая стоимость аннуитета. 5. Накопление единицы за период.	2. Текущая стоимость единицы. 4. Взнос на амортизацию единицы. 6. Фактор фонда возмещения.

Расчет факторов всех шести функций основан на использовании базовой формулы сложного процента или функции «Накопленная сумма единицы». Главным услови­ем, обеспечивающим математическую взаимосвязь между функциями, является предположение, что начисленный процент не снимается с де­позитного счета и капитализируется.

Теория и практика использования указанных функций денег, слож­ного процента базируется на ряде допущений:

1. Денежный поток, в котором все суммы различаются по величине, называют денежным потоком.

2. Денежный поток, в котором все суммы равновелики, называют аннуитетом.

3. Суммы денежного потока возникают через одинаковые промежутки времени, называемые периодом.

4. Суммы денежного потока могут возникать в конце периода, а также в начале и середине периода.

5. Предварительно рассчитанные таблицы сложного процента приме­нимы только к денежному потоку, возникающему в конце периода.

6. Доход, получаемый на инвестированный капитал, из хозяйствен­ного оборота не изымается, а присоединяется к основному капиталу.

7. Временная оценка денежных потоков учитывает инвестиционные риски, связанные с недвижимостью.

8. Риск — это вероятность получения в будущем дохода, совпадающе­го с прогнозной величиной.

9. Уровень риска должен иметь адекватную ставку дохода на вложен­ный капитал.

10. Ставка дохода на инвестиции — это процентное соотношение между чистым доходом и вложенным капиталом.

Рассмотрим подробнее шесть функций денег, шесть функций слож­ного процента.

1. Накопленная сумма единицы.

Данная функция позволяет определить будущую стоимость имеющейся денежной суммы исходя их предполагаемой ставки периодичности дохо­да, срока накопления и начисления процентов. Накопленная сумма еди­ницы — базовая функция сложного процента, позволяющая определить будущую стоимость при заданном периоде, процентной ставке и извест­ной сумме в будущем (рис. 1). Процесс начисления сложных процентов, позволяющий найти будущую ценность денег (FV), если известны их текущая ценность (РV), ставка процента (i), вре­менной интервал (t), называется компаундирование.

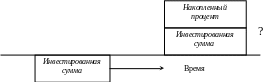
Рис. 1. Рост основной суммы по сложному проценту

Фактор накопления будущей стоимости основан на сложном про­центе. Сложный процент представляет геометрическую зависимость между первоначальным вкладом, процентной ставкой и периодом на­копления

где п — число периодов начисления.

Таким образом, сложный процент предполагает начисление процен­тов не только на основную сумму вклада, но и на соответствующую сум­му начисления процента. Это возможно только в случае реинвестирова­ния начисленных процентов, т. е. сохранения их на вкладе.

Период начисления по сложным процентам не всегда равен году, однако в условиях финансовой операции указывается не ставка за период, а годовая ставка с указанием периода начисления – номинальная ставка ( j ).

Номинальная ставка (nominal rate) – годовая ставка процентов, исходя из которой определяется величина ставки процентов в каждом периоде начисления, при начислении сложных процентов несколько раз в год.

Эта ставка

во-первых, не отражает реальной эффективности сделки;

во-вторых, не может быть использована для сопоставлений.

Если начисление процентов будет производиться m раз в год, а срок долга – n лет, то общее количество периодов начисления за весь срок финансовой операции составит:

N = n • m

Отсюда формулу сложных процентов можно записать в следующем виде:

FV = PV (1 + i/m)^{n m}

где i– годовая процентная ставка (коэфф.);

m – количество начислений в году;

n – срок вложения денежных средств, год.

Например, при квартальном накоплении применяется множитель: (1+i/4)^{n 4} , при месячном накоплении: ( 1 + i/12)^{n 12}

Для определения периода времени, необходимого для удвоения первоначального вклада, используется правило 72-х: удвоение первоначального вклада произойдет через число периодов, равное частному от деления 72 на процентную ставку соответствующего периода. Правило применимо для ставок дохода на капитал в интервале от 3% до 18%.

Например, если годовая ставка 18% и начисление процентов осуществляется ежегодно, удвоение вклада произойдет через 4 года:

72 : 18 = 4.

В ходе анализа эффективности двух и более вариантов инвестиций в различными интервалами наращения капитала необходимо использовать обобщающий финансовый показатель, позволяющий осуществить их объективную сравнительную оценку. Таким показателем является эффективная годовая процентная ставка, рассчитываемая по формуле:

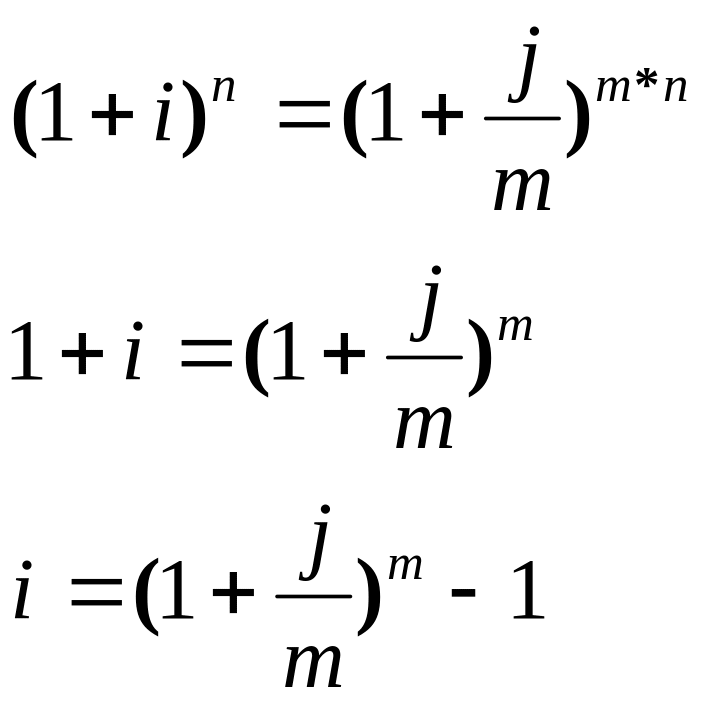
Эффективная годовая процентная ставка показывает, какая годовая ставка сложных процентов дает тот же результат, что и m – разовое начисление в год по ставке j/m, и позволяет сравнивать финансовые операции с различной частотой начисления и неодинаковыми процентными ставками. Именно эффективная процентная ставка характеризует реальную эффективность операции, т.к. измеряет тот реальный относительный доход, который получается в целом за год.