БАЛТИЙСКИЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ

ИМЕНИ ИММАНУИЛА КАНТА

Институт прикладной математики и информационных технологий

Кафедра математического моделирование и информационных систем

Направление бизнес-информатики

РЕФЕРАТ

По курсу: «Основы теории систем»

Тема: «Характеристика методов математического программирования. Линейное программирование.»

Выполнила студентка 1^ого курса

Кукса Анастасия Александровна

Преподаватель: Маклахова Ирина Сергеевна

гор. Калининград

2013 г.

Содержание:

1. Методы математического программирования

2. Линейное программирование

   • Задачи линейного программирования

   • Алгоритмы решения

   • Графический метод решения задачи линейного программирования

3. Нелинейное программирование

   • Методы решения задач

4. Целочисленное программирование

5. Динамическое программирование

   • Идея динамического программирования

   • Классические задачи динамического программирования

6. Теория графов

   • Некоторые задачи теории графов

   • Применение теории графов

7. Геометрическое программирование

8. Теория игр

9. Использованная литература

К математическому программированию относится:

1) Линейное программирование: состоит в нахождении экстремального значения линейной функции многих переменных при наличии линейных ограничений, связывающих эти переменные;

2) Нелинейное программирование: целевая функция и ограничения могут быть нелинейными функциями; 

3) Особым случаем в задачах линейного и нелинейного программирования является случай, когда на оптимальные решения накладывается условие целочисленности. Такие задачи относятся к целочисленному программированию;

4) Динамическое программирование: для отыскания оптимального решения планируемая операция разбивается на ряд шагов (этапов) и планирование осуществляется последовательно от этапа к этапу. Однако выбор метода решения на каждом этапе производится с учетом интересов операции в целом;

5) Теория графов: с помощью теории графов решаются многие сетевые задачи, связанные с минимальным протяжением сети, построение кольцевого маршрута и т.д.

6) Стохастическое линейное программирование.

Бывает много практических ситуаций, когда коэффициенты c_i целевой функции, коэффициенты a_ij в матрице коэффициентов, коэффициенты ограничений b_i - являются случайными величинами. В этом случае сама целевая функция становится случайной величиной, и ограничения типа неравенств могут выполняться лишь с некоторой вероятностью. Приходится менять постановку самих задач с учётом этих эффектов и разрабатывать совершенно новые методы их решения. Соответствующий раздел получил название стохастического программирования.

7) Геометрическое программирование.

Под задачами геометрического программирования понимают задачи наиболее плотного расположения некоторых объектов в заданной двумерной или трехмерной области. Такие задачи встречаются в задачах раскроя материала для производства каких-то изделий и т.п. Это - еще недостаточно разработанная область математического программирования и имеющиеся здесь алгоритмы в основном ориентированы на сокращение перебора вариантов с поиском локальных минимумов. 

8) Задачами теории массового обслуживания является анализ и исследование явлений, возникающих в системах обслуживания. Одна из основных задач теории заключается в определении таких характеристик системы, которые обеспечивают заданное качество функционирования, например, минимум времени ожидания, минимум средней длины очереди.

9) Теория игр пытается математически объяснить явления возникающие в конфликтных ситуациях, в условиях столкновения сторон. Такие ситуации изучаются психологией, политологией, социологией, экономикой.

Линейное программирование

Математическая дисциплина, посвящённая теории и методам решения экстремальных задач на множествах -мерного векторного пространства, задаваемых системами линейных уравнений и неравенств.

Линейное программирование является частным случаем выпуклого программирования, которое в свою очередь является частным случаем математического программирования. Одновременно оно — основа нескольких методов решения задач целочисленного и нелинейного программирования. Одним из обобщений линейного программирования является дробно-линейное программирование.

Многие свойства задач линейного программирования можно интерпретировать также как свойства многогранников и таким образом геометрически формулировать и доказывать их.

Задачи

Общей (стандартной) задачей линейного программирования называется задача нахождения минимума линейной целевой функции (линейной формы) вида:

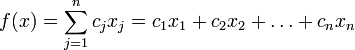
задача в которой фигурируют ограничения в форме неравенств, называется — основной задачей линейного программирования (ОЗЛП)

,

.

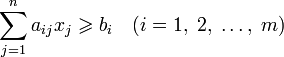Задача линейного программирования будет иметь канонический вид, если в общей задаче вместо первой системы неравенств имеет место система уравнений с ограничениями в форме равенства:

,

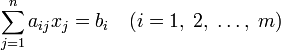Основную задачу можно свести к канонической путём введения дополнительных переменных.

Задачи линейного программирования наиболее общего вида (задачи со смешанными ограничениями: равенствами и неравенствами, наличием переменных, свободных от ограничений) могут быть приведены к эквивалентным (имеющим то же множество решени0й) заменами переменных и заменой равенств на пару неравенств.

Легко заметить, что задачу нахождения максимума можно заменить задачей нахождения минимума, взяв коэффициенты с обратным знаком.