1. Модель адаптивных ожиданий

Ожидания играют существенную роль в экономической активности, что затрудняет моделирование соответствующих экономических процессов. Особенно серьезна эта проблема на макроэкономическом уровне. Например, при прогнозировании объема инвестиций требуется учитывать не только процентную ставку, но и экономическую политику государства, на основе которой потенциальные инвесторы принимают свои решения.

Одним из направлений решения рассматриваемой задачи является модель адаптивных ожиданий. В данной модели происходит постоянная корректировка ожиданий на основе получаемой информации о реализации исследуемого показателя. Если реальное значение показателя оказалось больше ожидаемого, то ожидаемое в следующем периоде корректируется в сторону увеличения. В противном случае – наоборот. При этом величина корректировки должна быть пропорциональна разности между реальным и ожидаемым значениями.

В данной модели в уравнение регрессии в качестве объясняющей переменной вместо текущего значения вводится ожидаемое значение :

(7.11)

Так как ожидаемые значения не являются фактически существующими, выдвигается предположение, что эти значения связаны следующим соотношением:

(7.12)

Модель (7.12) называется моделью адаптивных ожиданий (или моделью обучения на ошибках). Коэффициент называется коэффициентом ожидания. Иногда в модели (7.12) вместо текущего значения используют предыдущее значение :

(7.13)

Перепишем соотношение (7.12) в виде:

(7.14)

Из (7.14) видно, что ожидаемое значение является взвешенным средним между текущим значением и его ожидаемым значением в предыдущий период с весами и соответственно. Если , то ожидания являются неизменными: . Если , то , что означает мгновенно реализуемые ожидания.

Подставим (7.14) в (7.11), в результате чего получим:

(7.15)

Определим по (7.15) значение в предыдущий момент времени, умноженное на :

(7.16)

Из (7.15) отнимем (7.16):

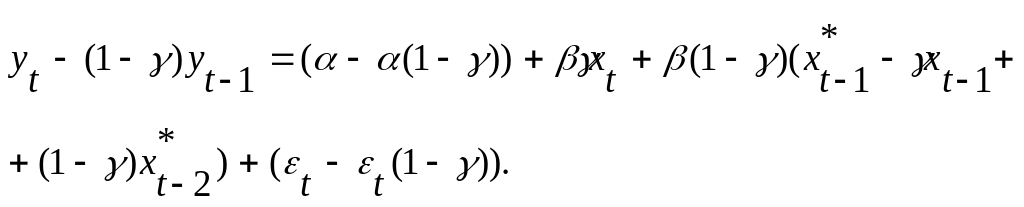
Так как из (7.14) , то:

(7.17)

где .

На практике при оценивании параметров авторегрессионного уравнения (7.17) вначале оценивается параметр , затем коэффициент при , затем свободный член .

Рассмотрим случай, когда зависимая переменная в текущий момент времени связана с ожидаемым в следующий период времени значением (например, зависимость спроса на деньги от ожидаемой процентной ставки), т.е.:

(7.18)

Допустим, что ожидаемое в следующий период времени значение переменной определяется как взвешенное среднее ее реального и ожидаемого значения в текущий период времени (аналогично 7.14):

(7.19)

Следовательно, . Отсюда (7.19) примет вид:

Из (7.19) следует, что , и т.д. С учетом этого (7.19) примет вид:

(7.20)

Подставив (7.20) в (7.18), получаем:

(7.21)

Обозначив через и через , получаем соотношение (7.6).