Задача 5

Задана консольная балка постоянной жесткости (EJ = const), рис. 5.

Требуется:

Определить по правилу Верещагина вертикальное перемещение точки В

Данные взять из табл. 5.

Таблица 5

Схема №	q, кН/м	F, кН	M, кН·м	l, м

Рис. 5

Обозначим на схеме балки:

т. А – жесткая заделка,

т. В – свободный конец балки,

С – точка приложения силы или момента либо граница участка действия распределенной нагрузки, расположенные между концами балки.

1. Эпюры изгибающего момента от отдельных видов нагрузки (грузовые).

а) от распределенной нагрузки:

Сеч. В: М_и = 0 кН,

сеч. С: М_и = = = кНм,

сеч. А: М_и = = = кНм.

Построим эпюру.

б) от силы (момента):

Сеч. В: М_и = = кНм,

сеч. А: М_и = = = кНм.

Если сила или момент приложены не на конце балки:

сеч. С (………): М_и = = = кНм,

сеч. С (………): М_и = = = кНм,

Построим эпюру.

в) приложим в т. В единичную нагрузку, направленную вверх, и построим эпюру изгибающего момента и от нее:

сеч. В: М_и = 0 кН,

сеч. А: М_и = = = м.

Построим эпюру.

2. Перемещение т. В от распределенной нагрузки. Вычислим площадь эпюры изгибающего момента, применяя готовые формулы (h – высота криволинейного треугольника, a – длина основания:

S = ah/3 = = кНм²,

координата ее центра тяжести

z = a/4 = = м,

ордината (высота графика) эпюры от единичной нагрузки под центром тяжести грузовой эпюры

у_с = 2l - z = = м,

перемещение т. В равно

у₁ = м.

3. Перемещение т. В от силы (момента). Вычислим площадь эпюры изгибающего момента, применяя готовые формулы:

S = = = кНм²,

координата ее центра тяжести

z = = = м,

ордината (высота графика) эпюры от единичной нагрузки под центром тяжести грузовой эпюры

у_с = 2l - z = = м,

перемещение т. В равно

у₂ = м.

4. Полное перемещение в точке В:

у = у₁ + у₂ = = м.

Отрицательный знак говорит о перемещении т. В в направлении, противоположном единичной нагрузке.

Задача 6

Вал трансмиссии (рис. 6) делает n оборотов в минуту и передаёт мощность N кВт.

Требуется:

1.Определить моменты, приложенные к шкивам 1 и 2.

2.Построить эпюру крутящих моментов Мкр.

3.Определить окружные усилия t₁ и t₂, действующие на шкивы 1 и 2, по найден­ным моментам и заданным диаметрам D₁ и D₂.

4.Построить эпюру изгибающих моментов.

5.Найти опасное сечение и определить величину максимального расчётного мо­мента по третьей теории прочности.

6.Подобрать диаметр вала d при [σ_р] = 70 МПа =70·10⁶ Па.

Данные взять из табл. 6

Таблица 6

№ строки	Схема	N, кВт	п, об/мин	а, м	в, м	с, м	D1, м	D2, м	а1, градус	а2, градус

N= ……·10³ Вт

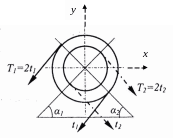
Рис. 6

Решение.

Угловая скорость вала:

= рад/с.

Моменты приложенные к шкивам:

= Нм.

Эпюра крутящих моментов:

M_к,1 = Нм,

M_к,2 = Нм ,

M_к,3 = Нм.

Окружные усилия. Из уравнения равновесия моментов, приложенных к шкиву:

следует

= Н,

= Н,

T₁ = 2t₁ = = H,

T₂ = 2t₂ = = H.

Разложим силы натяжения ремней на составляющие:

= H,

= H,

= H,

= H,

= H,

= H,

= H,

= H.

Нарисуем действующие силы.

Составим уравнения равновесия для вертикальных сил:

. = 0

= 0,

Решим уравнения:

R_Ву = = = Н,

R_Ау = = = Н.

Эпюра изгибающего момента. На концах вала он равен нулю.

От левого конца сеч. …..: М_х = = = Нм,

от правого конца сеч. ……: М_х = = = Нм.

Нарисуем эпюру.

Составим уравнения равновесия для горизонтальных сил:

= 0

= 0,

Решим уравнения:

R_Вх = = = Н,

R_Ах = = = Н.

Эпюра изгибающего момента. На концах вала он равен нулю.

От левого конца сеч. …..: М_у = = = Нм,

от правого конца сеч. ……: М_у = = = Нм.

Нарисуем эпюру.

Опасные сечения: в т. ….. и……. .

Вычислим расчетные моменты в этих сечениях по третьей теории прочности:

в т. …..

= Нм.

в т. …..

= Нм.

Выберем наибольшее Нм.

Диаметр вала подберем из условия прочности:

, где =70МПа=70∙10⁶Па

.

Для круга: _,

отсюда

·10^-2 м = мм.