
Задача 4
Даны две схемы стальных балок (рис. 4, а, б)
Требуется:
Для схемы «а»:
Построить эпюры поперечной силы Q и изгибающего момента M.
Проверить прочность по нормальным напряжениям в балке сложного поперечного сечения, уже рассмотренного в задаче 1.
3. Вычислить коэффициент использования прочности стали балки.
Определить прогиб конца консоли аналитическим методом.
Для схемы «б»:
Построить эпюры поперечной силы Q и изгибающего момента M.
Подобрать сечения следующей формы: прямоугольное (h/b = k); круглое; кольцевое (α = d/D); двутавровое.
Оценить эффективность формы сечения.
Для всех вариантов принять:
допускаемое
напряжение ![]() =
240 МПа = 240·106
Па,
=
240 МПа = 240·106
Па,
модуль упругости (модуль Юнга) E = 2∙105 МПа.
Остальные данные взять из табл. 4
Таблица 4
Схема № |
а1, м |
а2, м |
q, кН/м |
F, кН |
М, кН·м |
k |
α |
|
|
|
|
|
|
|
|
Рис.
4, а
Решение.
Схема «а» (рис.4, а ). Нарисуем балку так, чтобы опора была с левой стороны. Перевернуть зеркально вместе с нагрузкой, если в задании она изображена наоборот.
Определяем опорные реакции балки. Заданная балка зафиксирована жесткой заделкой. Характер прикладываемой нагрузки обуславливает необходимость определения только вертикальных реакций опор
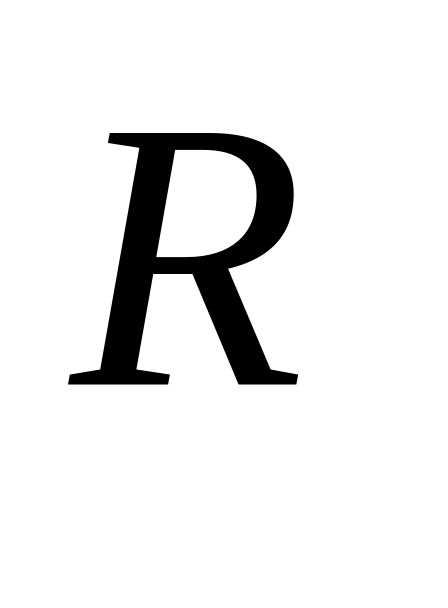 и
и
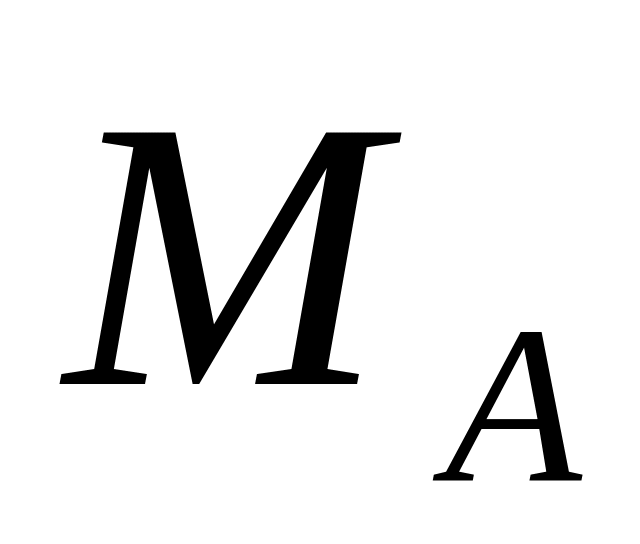 ,
так как горизонтальная составляющая
реакции в опоре А равна нулю
(
,
так как горизонтальная составляющая
реакции в опоре А равна нулю
(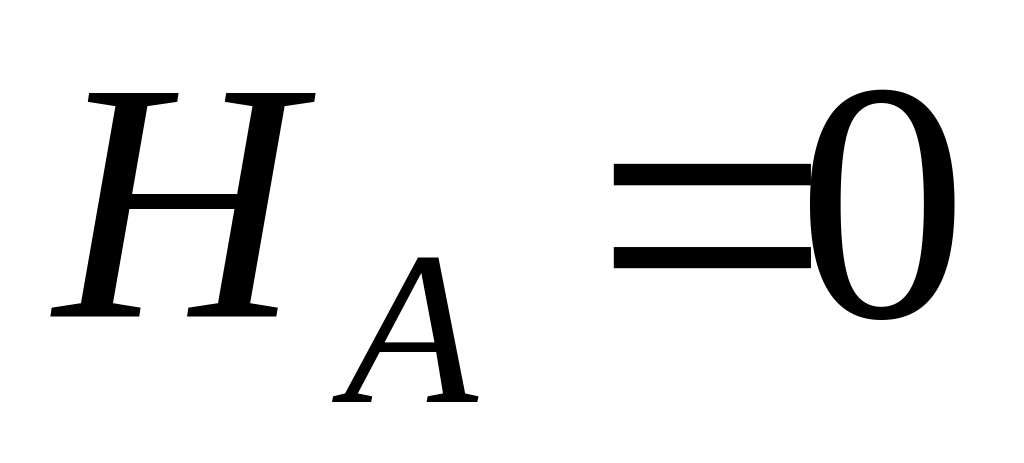 ).Направим
момент
против часовой стрелки, а силу
–
вверх.
).Направим
момент
против часовой стрелки, а силу
–
вверх.
![]() =
0
=
0
![]() = 0,
= 0,
Решим уравнения:
R = = = кН,
МА = = = кНм.
Эпюра поперечной силы. Для консольной балки строится, начиная со свободного конца.
Сеч. В: Q = = кН,
сеч. С (справа): Q = = = кН,
сеч. С (слева): Q = = = кН,
сеч. А: Q = = = кН.
Нарисуем эпюру (рис. 4, а).
Эпюра изгибающего момента. Строится, начиная со свободного конца.
Сеч. В: Ми = = кН,
сеч. С (справа): Ми = = = кНм,
сеч. С (слева): Ми = = = кНм,
сеч. А: Ми = = = кНм.
Нарисуем эпюру (рис. 4, а).
Проверка на прочность.
Максимальный (по модулю) изгибающий момент найдем на эпюре:
|Mи|max = кНм = ∙103Нм.
Момент сопротивления сечения изгибу из задачи 1:
Wx = см3 = ·10-6 м3.
Максимально нормальное напряжение найдем из формулы
![]()
Фактический коэффициент запаса прочности:
![]() = > 1 запас
прочности достаточный (или недостаточный,
если неравенство не выполняется).
= > 1 запас
прочности достаточный (или недостаточный,
если неравенство не выполняется).
5. Прогиб конца балки найдем с помощью универсального уравнения прогибов
![]()
Условия
на левом конце балки:
![]() ,
,
В нашем случае
![]()
Знаки определяются по правилу знаков для изгиба (при отсутствии какой-либо величины слагаемое выбрасывается).
Координата правого (свободного) конца z = a1 + a2 = = м,
координата момента М: а = = м,
координата силы F: в = = м,
координата участка действия равномерно-распределенной нагрузки:
c = = м,
d = = м,
момент инерции сечения берется из задачи 1:
Jx = см4 = ·10-8 м4.
E = 2·1011Па
Подставим данные
Найдем прогиб
y = м = мм.
Схема «б» (рис.4, б ).
1. Определяем
опорные реакции балки. Заданная балка
зафиксирована в двух сечениях с помощью
шарнирно-подвижной и шарнирно-неподвижной
опор. Характер прикладываемой нагрузки
обуславливает необходимость определения
только вертикальных реакций опор
![]() и
и
![]() ,
так как горизонтальная составляющая
реакции в опоре А равна нулю (
).
,
так как горизонтальная составляющая
реакции в опоре А равна нулю (
).
. = 0
= 0,
Решим уравнения:
RВ = = = кН,
RА = = = кН.
Эпюра поперечной силы:
Сеч. C: Q = = кН,
сеч. В (справа): Q = = = кН,
сеч. B (слева): Q = = = кН,
сеч. А: Q = = = кН.
Нарисуем эпюру (рис. 4, б).
Эпюра изгибающего момента.
Сеч. C: Ми = = кН,
сеч. B (справа): Ми = = = кНм,
сеч. B (слева): Ми = = = кНм,
сеч. А: Ми = = = кНм.
Нарисуем эпюру (рис. 4, б).
Рис. 4, б
Определение размеров сечений. Максимальный (по модулю) изгибающий момент найдем на эпюре:
|Mи|max = кНм = ∙103Нм.
Момент сопротивления
сечения изгибу из условия прочности![]()
![]() = ·10-3
м3.
= ·10-3
м3.
Подбираем прямоугольное сечение. Соотношение сторон
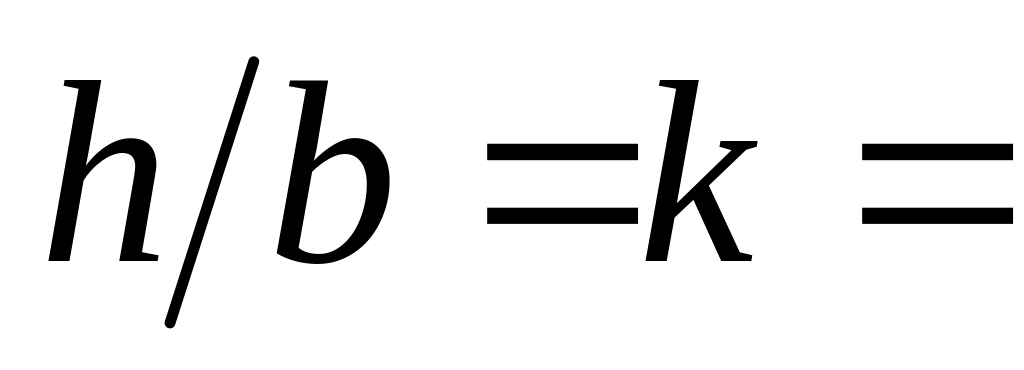 .
.
Так как для
прямоугольного сечения момент
сопротивления относительно оси X
:
![]() и по условию
и по условию
![]() ,
то:
,
то:
![]()
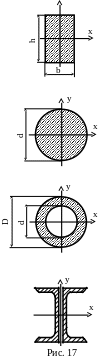 ,
откуда
,
откуда
![]() = ·10-1
м = см,
= ·10-1
м = см,
![]() = см.
= см.
Подбираем круглое сечение.
Для круглого
сечения осевой момент сопротивления
![]() ;
тогда
;
тогда
![]() =
·10-1 м = см.
=
·10-1 м = см.
.
Подбираем кольцевое сечение. Отношение диаметров
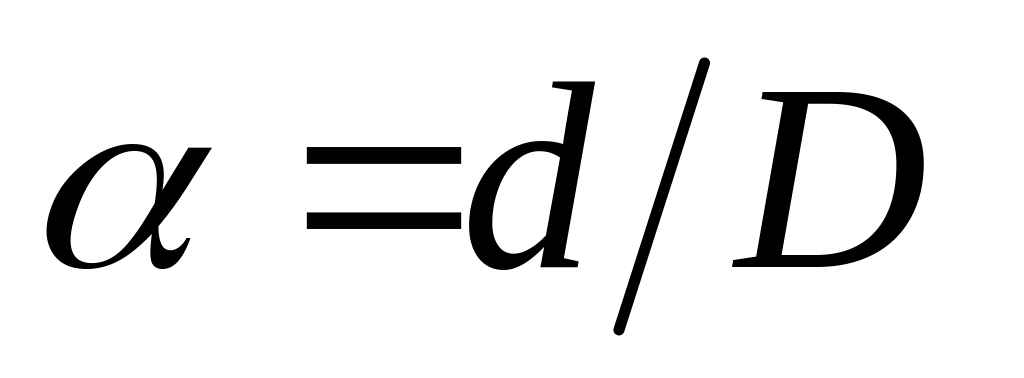 .
.
Для кольцевого
сечения осевой момент сопротивления
![]() .
Тогда
.
Тогда
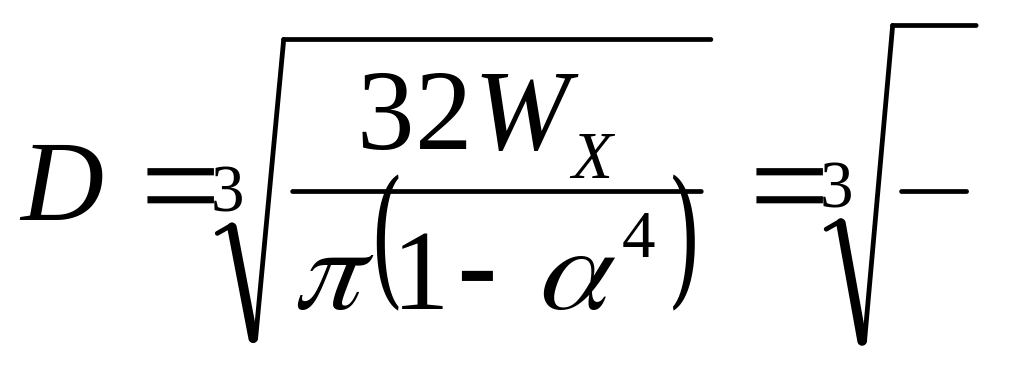
 = ·10-1
м = см,
= ·10-1
м = см,
![]() =
см.
=
см.
.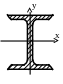
Подбираем двутавровое сечение.
Момент сопротивления двутавра должен быть не менее требуемого WХ = см3.
По ГОСТ 8239-89 принимаем двутавровую балку № … с ближайшим бóльшим значением момента сопротивления, значение которого отвечает условию проектировочной задачи:
![]() см3.
см3.
3. Оцениваем эффективность формы сечения.
Для чего сравниваем площади всех подобранных сечений.
![]() = см2,
= см2,
![]() = см2,
= см2,
![]() = см2,
= см2,
см2.
Наиболее эффективной формой сечения балки (балка с наименьшим весом) является двутавровое сечение, наименее эффективной – круглое сплошное сечение.
