
- •Алматинский институт энергетики и связи 2004г.
- •1.6 Используя программный продукт «Пакет экономических расчетов» рассмотрим решение примера 1.
- •3.3.2 Работа нагруженного трансформатора
- •3.3.3 Мощность трансформатора и к.П.Д.
- •I Электромеханическое преобразование энергии не может осуществляться с кпд, равным 100%.
- •II Все эп обратимы, т.Е. Они могут работать как в двигательном, так и в генераторном режимах.
- •III Электромеханическое преобразование энергии осуществляется полями, неподвижными относительно друг друга.
- •4.4 Математические модели электромагнитных процессов в обобщенной асинхронной машине
4.4 Математические модели электромагнитных процессов в обобщенной асинхронной машине
Уравнения математической модели асинхронного двигателя в токах имеет вид /3/
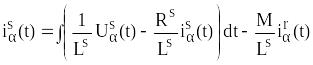 (4.7)
(4.7)
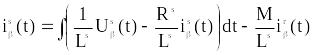 (4.8)
(4.8)
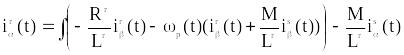 (4.9)
(4.9)
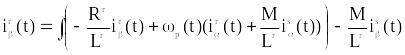 (4.10)
(4.10)
![]() (4.11)
(4.11)
![]() (4.12)
(4.12)
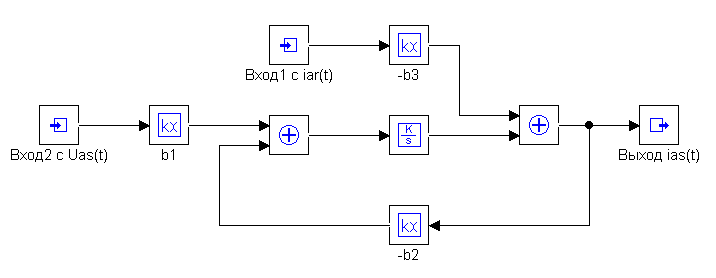
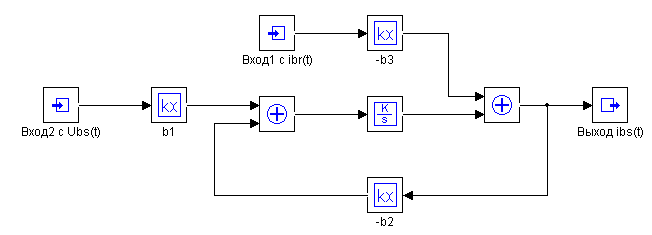
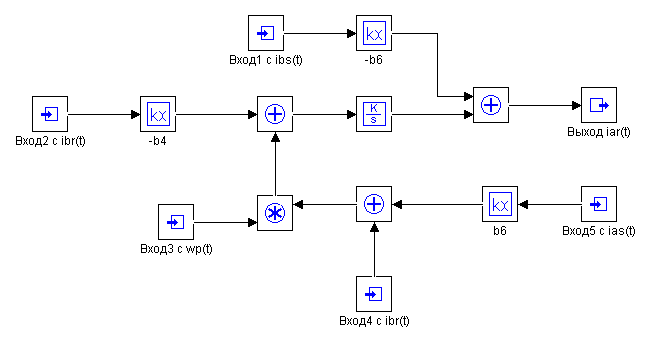
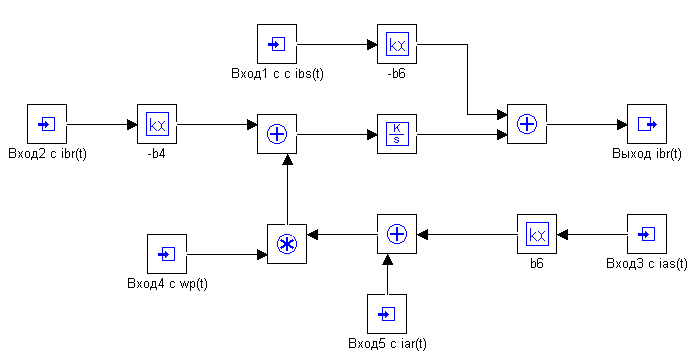
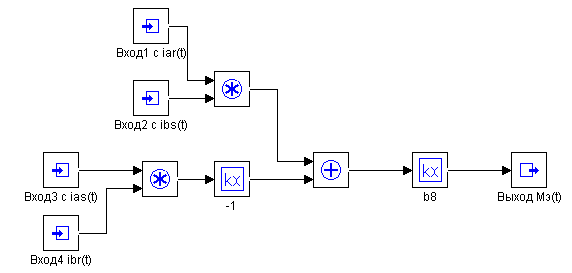
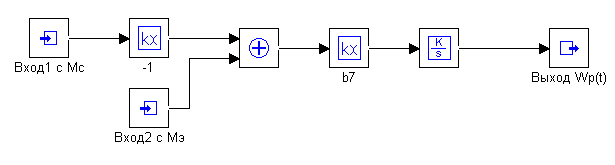
Схема модели электромагнитных и электромеханических процессов (по току) асинхронного двигателя (4.7)-(4.12) приводятся на рисунке 4.4.
Схема модели электромагнитных и электромеханических процессов (по току) асинхронного двигателя
а)
|
б)
|
в)
|
г)
|
е)
|
д)
|
ж)
|
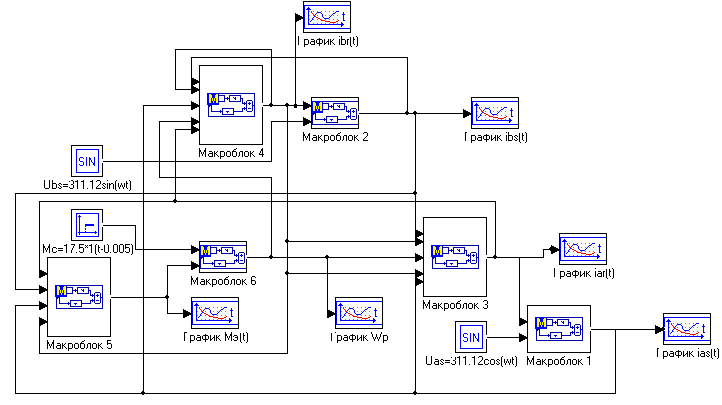
Рисунок 4.4
а) – Макроблок №1, б) – Макроблок №2, в) – Макроблок №3, г) – Макроблок №4, д) – Макроблок №5, е) – Макроблок №6, ж) – Схема модели.
Программный аналог модели (4.7)-(4.12) в среде программной системы MVTU получил имя LAB16_1.prj.
Исходные данные (для нечетных вариантов) приводятся в таблице 4.1.
Примечание: Rr = rαr = rβr; Rs = rαs = rβs; Ls = Lαs = Lβs; Lн = Lαн = Lβн
Условия математической модели асинхронного двигателя в потокосцеплениях имеет вид
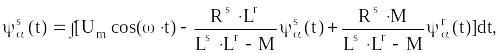 (4.13)
(4.13)
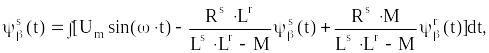 (4.14)
(4.14)
 (4.15)
(4.15)
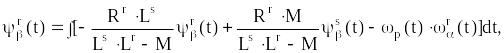 (4.16)
(4.16)
![]() , (4.17)
, (4.17)
![]() , (4.18)
, (4.18)
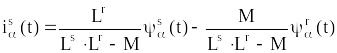 , (4.19)
, (4.19)
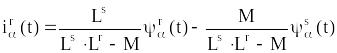 , (4.20)
, (4.20)
 , (4.21)
, (4.21)
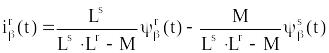 . (4.22)
. (4.22)
На рисунках 4.4 введены следующие обозначения в модели по току
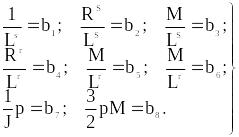 (4.23)
(4.23)
В модели на потокосцепление
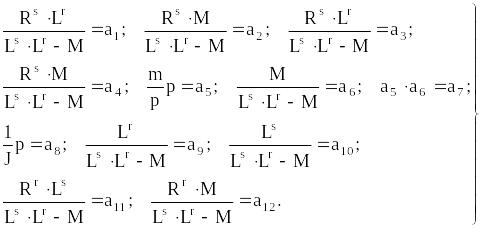 (4.25)
(4.25)
Исходные данные модели асинхронного двигателя в потокосцеплениях (для четных вариантов) приводятся в таблице 4.1.
4.5 Содержание лабораторной работы
4.5.1 По заданию преподавателя рассчитать коэффициенты ai и bi для заданных преподавателем вариантов l, l+1, где l - нечетный номер из таблицы 4.1 (т.е. для модели по току и по потокосцеплению)
4.5.2 Провести моделирование процессов в асинхронном двигателе для математической модели по току и потокосцеплению для двух значений тормозного момента:
Mc(t)=Mн×1(t-t), (4.26)
Me(t)=0.5×Mн×1(t-t), Mн=17.5 Н×м, t=0.005. (4.27)
Для экспериментов выбран трехфазный короткозамкнутый двигатель А 42‑6. Двигатель имеет следующие номинальные данные Р2н=1.7 кВт,
Uн=220 В, Iн=7.5 А, nн=930 об/мин, Мн=9550Р/n=17.5 Н×м. Параметры двигателя при рабочей температуре 750С:
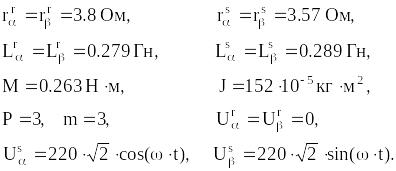
4.5.3
Принять в качестве напряжений на обмотках
статора следующие значения: w=2×pf,
f=50,
Uм=Uн×![]() =220×
.
=220×
.
4.5.4 В модели по току результатом исследований, представленных в виде временных зависимостей, принять:
![]() .
.
4.5.5 Модель по потокосцеплению студенту предлагается разработать самостоятельно. В модели по потокосцеплению результатом исследований, представленных в виде временных зависимостей, принять:
![]()
![]()
4.5.6 Провести анализ результатов полученных в пп. 4.5.4, 4.5.5.
4.6 Контрольные вопросы
4.6.1 Сформулируйте и поясните первый закон электромеханического преобразования энергии.
4.6.2 Сформулируйте и поясните второй закон электромеханического преобразования энергии.
4.6.3 Сформулируйте и поясните третий закон электромеханического преобразования энергии.
4.6.4 От чего зависит электромагнитный момент асинхронного двигателя?
4.6.5 Какая связь существует между электромагнитным моментом асинхронного двигателя и динамическим моментом электропривода с асинхронным двигателем?
4.7 Список файлов к лабораторной работе № 4
LAB16_1.prj — в среде MVTU.
4.8 Контрольный пример
Контрольный пример по лабораторной работе № 4 приводится в файле LAB16_1K.prj.
Таблица 4.1 - Исходные данные
№№ п/п |
Параметры двигателя |
|||||
|
|
|
M |
|
p |
|
|
|
|
|
|
|
|
*
