АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ

И СВЯЗИ

Кафедра электроснабжения промышленных предприятий

МАТЕМАТИЧЕСКИЕ ЗАДАЧИ ЭНЕРГЕТИКИ И КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ

Методические указания к выполнению лабораторных работ

для студентов электроэнергетических специальностей

Алматы 2004

АЛМАТИНСКИЙ ИНСТИТУТ ЭНЕРГЕТИКИ И СВЯЗИ

Кафедра электроснабжения промышленных предприятий

УТВЕРЖДАЮ

Проректор по учебно-методической работе

______________________

“___”_________________2004 г.

МАТЕМАТИЧЕСКИЕ ЗАДАЧИ ЭНЕРГЕТИКИ И

КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ

Методические указания к выполнению лабораторных работ

для студентов электроэнергетических специальностей

СОГЛАСОВАНО Рассмотрено и одобрено на

Начальник УМО заседании кафедры ЭПП

________________ Протокол № _5__

“___”___________2004г. от “_09_”_января__ 2004г.

Зав. кафедрой ЭПП,

д.т.н., профессор

_____________А.В. Болотов

Редактор Составители:

Старший преподаватель

________________ кафедры ЭПП

__________Н.А. Туканова

“___”___________2004г. Инженер кафедры ЭПП

___________М.М. Махмат

Алматы 2004

СОСТАВИТЕЛИ: Н.А. Туканова, М.М. Махмат. Математические задачи энергетики и компьютерное моделирование. Методические указания к выполнению лабораторных работ для студентов электроэнергетических специальностей - Алматы, АИЭС, 2004. - 34 с.

Методические указания по курсу «Математические задачи энергетики и компьютерное моделирование», включают задания на выполнение лабораторных работ, исходные данные, указания и перечень рекомендуемой литературы.

Методические указания предназначены для студентов очного и заочного обучения.

Ил. 6, табл. 14, библиогр. - 11 назв.

Рецензент: к.т.н., доцент С.А. Бугубаев

Печатается по плану издания Алматинского института энергетики и связи на 2004 год.

С

Алматинский институт энергетики и связи 2004г.

В ведение

С развитием промышленности получили дополнительное развитие электрические системы. Чтобы управлять и развивать электрические системы на помощь приходят математические методы прогнозирования, анализа и оптимизации. Решение оптимизационных задач очень важно для инженера-энергетика. Здесь необходимо учесть, что управление энергосистемой и её проектирование должны обеспечивать не только необходимые значения параметров режима, но и максимальную экономичность режима системы в целом при полном удовлетворении потребителей электроэнергией.

Зная алгоритм решения задачи линейного программирования, можно составить программу ее решения на ЭВМ. На сегодняшний день существуют много языков программирования (Pascal, Delhpi, С++, FoxPro, Basic)с помощью которых можно составлять программы для решения задач линейного программирования, математической статистики и т.д. Однако такие программы составить достаточно сложно, поэтому студентам предлагается решить поставленные задачи (на симплекс метод, транспортные задачи, задачи динамического программирования, сетевого моделирования) с помощью специально разработанной программы ПЭР (Пакет экономических расчетов).

При расчете оптимизационных режимов электроэнергетических систем неоценимую помощь оказывают универсальные компьютерные программы-симуляторы электрических систем. Они позволяют на модели произвести экспериментальные исследования, которые сложно и трудоемко выполнять в реальной системе.

Лабораторная работа № 1

Решение систем линейных уравнений и нахождение оптимальных решений с помощью Симплекс метода

1.1 Цель работы

Целью настоящей работы является решение математических задач энергетики с помощью линейного программирования.

1.2 Порядок проведения работы

1.2.1 Найти первоначальный опорный план.

1.2.2 Составить симплекс - таблицу (см. пример таблица 1.6.1).

1.2.3 Определить оптимальность опорного плана и при необходимости перейти к новому опорному плану.

1.2.4 Определить направляющие столбцы и строки.

1.2.5 По методу Жордана - Гаусса определить положительные компоненты нового опорного плана и записать в новой симплекс-таблице.

1.2.6 Проверить план на оптимальность. Если план не оптимален, то вернуться к пункту 1.2.3, а в случае оптимального плана или неразрешимости плана процесс решения заканчивается.

1.3 Оформление результатов работы

Отчет должен содержать:

1.3.1 Исходные данные в виде уравнения функции и системы линейных уравнений.

1.3.2 Первоначальный опорный план, записанный в виде симплекс-таблицы.

1.3.3 Все этапы решения (все симплекс – таблицы) до получения оптимального плана или неразрешимости плана.

1.4 Методические указания

Симплексный метод решения задачи линейного программирования основан на переходе от одного опорного плана к другому, при котором значение целевой функций возрастает (при условии, что данная задача имеет оптимальный план и каждый ее опорный план является невырожденным). Рассмотрим задачу, для которой требуется найти максимальное значение функции

п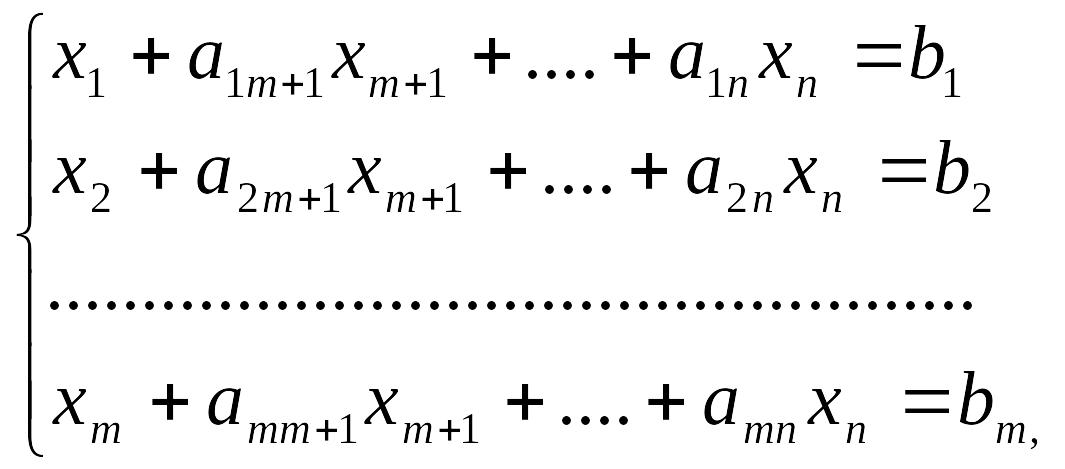 ри условиях

,

где, ,( и )- заданные постоянные числа. Векторная форма данной задачи имеет следующий вид

(1.1)

при условиях

(1.2)

( ), (1.3)

где , , , , , .

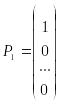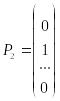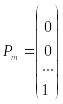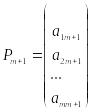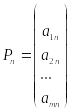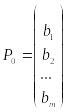Так как , то по определению опорного плана является опорным планом данной задачи (последние компонентов вектора равны нулю). Этот план определяется системой единичных векторов которые образуют базис -мерного пространства. Поэтому каждый из векторов а также вектор могут быть представлены в виде линейной комбинации векторов данного базиса. Пусть . Так как векторы - единичные, то и , а .

Признаки оптимальности опорного плана:

1) Опорный план задачи (1.2)-(1.3) является оптимальным, если для любого ( ).

2) Если для некоторого и среди чисел нет положительных , то целевая функция (1.1) задачи (1.2)-(1.3) не ограничена на множестве ее планов.

3) Если опорный план задачи (1.2)-(1.3) не вырожден и , но среди чисел есть положительные (не все ), то существует опорный план такой, что .

1.4.1 Этапы нахождение оптимального опорного плана симплекс-методом:

1 Найти опорный план

2 Составить симплекс – таблицу (таблица 1.6.1)

3 Проверить опорный план на оптимальность. Если имеется ли хотя бы одно отрицательное число , то либо устанавливают неразрешимость задачи, либо переходят к новому опорному плану. Если нет, то найденный опорный план оптимален.

4 Найти направляющие столбец и строку. Направляющий столбец определяется наибольшим по абсолютной величине отрицательным числом , а направляющая строка - минимальным из отношений компонент столбца вектора к положительным компонентам направляющего столбца.

5 По методу Жордана - Гаусса определить положительные компоненты нового опорного плана, коэффициенты разложения векторов по векторам нового базиса и числа . Все числа записать в новой симплекс-таблице.

6 Проверить план на оптимальность. Если план не оптимален, то возвращаемся к 4 этапу, а в случае оптимального плана или неразрешимости плана процесс решения заканчивается.

1.5 Задание и исходные данные

Требуется найти максимальное или минимальное значение функции

при условиях

,

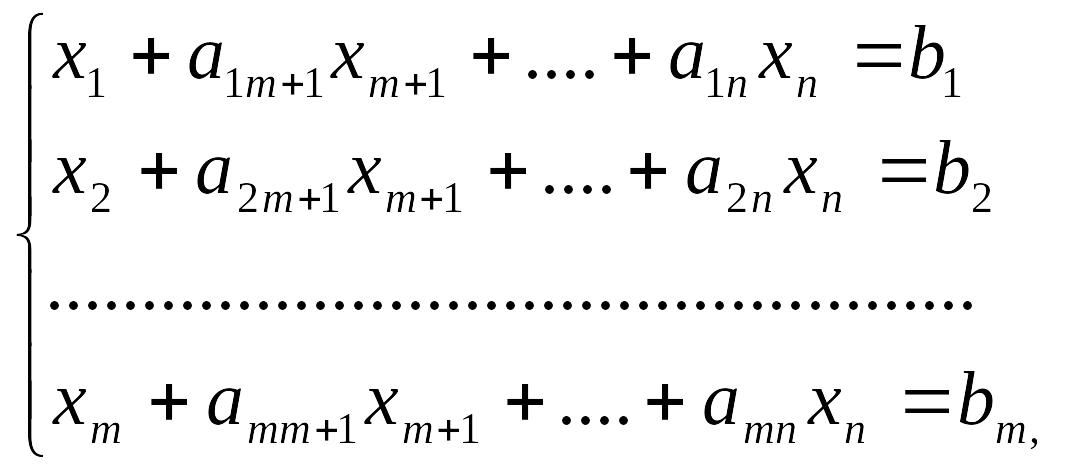где, и f(x) min или max студент выбирает под начальной буквой фамилий, а элементы , и знаки ограничений выбираем по последней цифре номера зачетной книжки.

Таблица 1.5.1 – Исходные данные

Начальная буква фамилии студента	А, Д	Б, Е	В, Г, Я	Ж, З, И, Л	К	М, О	Н, П	Р, Т, У, Ф	С, Ч	Х, Ш, Щ, Э, Ю
Элементы целевой функций
C1	1	2	1	-1	5	2	2	1	-4	5
C2	-2	1	5	3	2	1	3	-2	5	1
C3	3	-1	4	2	-1	-1	6	-3	6	-3
C4	10	-1	-6	-	-	-1	3	-	-	1
f(x)	max	min	max	min	max	min	max	min	max	min