Вопрос 26.

Равновесие между водой и гидрофобными жидкостями. Коэффициенты растворимости и распределения органических компонентов и методы их определения.

Параметры равновесия

Подземный газ и вода в геологических условиях обмениваются преимущественно газовыми и летучими органическими компонентами. При высоких давлении и температуре в этом процессе могут участвовать и вещества, которые в нормальных условиях находятся в жидком или даже в твердом состоянии. Поступление этих компонентов в подземный газ называют улетучиванием или испарением, а их абсорбцию водой - растворением.

Этот массообмен всегда направлен в сторону среды с более низкими величинами фугитивности или парциальных давлений. В связи с этим в качестве показателя степени насыщения воды компонетом i относительно подземного газа можно использовать отношение 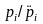, а в качестве индекса неравновесности - 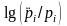. При равновесии степень насыщения равна 1, а индекс – нулю. Если степень насыщения больше 1 (индекс <0), вода перенасыщена относительно подземного газа, если меньше (индекс > 0), вода недонасыщена.

При отсутствии парциальных давлений (фугитивностей), сравнивают фактические концентрации отдельных компонентов в разных средах, как правило, в мольных долях. Если 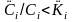, то компонент i мигрирует из воды в подземный газ, а если 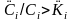, то из подземного газа в воду. При достижении равновесия .

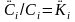В связи с этим для оценки поведения газовых и летучих компонентов на границе воды и подземного газа необходимо сравнить либо их парциальные давления, либо концентрации в этих средах.

При полном равновесии суммы парциальных давлений компонентов в воде и в подземном газе равны:

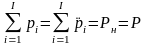, (II‑1)

и соблюдается равенство (II-359). В условиях низких давлений (около 0,1 МПа) и температур парциальные давления в составе подземного газа определяется по уравнению (II-374).

Парциальное давления любого газового компонента в воде в тех же условиях можно определить с помощью коэффициентов растворимости Гери или Бунзена, определенных для парциальных давлений 1 атм. При наличии величин коэффициента растворимости Генри парциальное давление компонента i определяется по уравнению (II-352). Величины коэффициентов растворимости Генри можно найти в справочной литературе (Таблица II-33). Однако эти величины применимы только для разбавленных растворов при давлении около 1 атм в ограниченном диапазоне температур.

Рисунок II-1. Коэффициенты растворимости Генри при давлении 0,1 МПа в ат·м³·моль^-1 (по данным Мишниной Т.А. и др., 1961, Pagenkopf, 1978)

Температура, oC	O2	N2	CO2	H2S	CH4	C2H6	C3H8	He	Ar
0	0,46	0,95	0,013	0,005	-	-	-	-	-
5	0,52	1,07	0,016	0,006	0,46	-	-	2,38	0,46
10	0,58	1,20	0,019	0,007	0,53	0,39	0,41	2,46	0,54
15	0,66	1,33	0,022	0,008	0,60	0,46	0,49	2,55	0,61
20	0,73	1,45	0,026	0,009	0,67	0,52	0,58	2,61	0,67
25	0,79	1,56	0,030	0,010	0,74	0,59	0,68	2,64	0,73
30	0,86	1,65	0,034	0,011	0,82	0,66	0,77	2,67	0,79
35	0,92	1,78	0,038	0,012
40	0,97	1,88	0,043	0,013	0,94	0,78	0,97	2,67	0,90
50	1,07	2,02	0,052	0,016	1,03	0,90	1,17	2,61	1,00
60	-	2,08	-	-	1,11	1,00	1,34	2,49	1,07
70	-	2,11	-	-	1,17	1,17	1,49	2,38	1,15

Гораздо чаще используется коэфффициент растворимости Бунзена. При его использовании парциальное давление определяется по уравнению:

. (II‑2)

Коэффициенты растворимости Бунзена для дистиллированной воды в нормальных или стандартных условиях, которые часто называемые просто растворимостью, можно найти с указанием температуры в справочной литературе. Их величины для минерализованных вод можно рассчитать, либо используя непосредственно коэффициенты Савченко, либо с помощью уравнений Рея Вайса. В первом случае

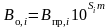. (II‑3)

Здесь S_i – коэффициент Савченко, величины которого можно найти в таблице II-34.

Рисунок II-2. Величины коэффициентов И.М. Сеченова (Мишнина Т.А., и др., 1961.)

Температура, oC	Коэффициенты Сеченова, Si
	O2	CH4	C2H6	C3H8	nC4H10	N2	Ar	He
0	0,180	-	-	-	-	-	-	-
5	0,168	0,172	-	-	-	-	0,169	0,073
10	0,160	0,159	0,188	0,219	0,247	0,160	0,155	0,074
15	0,156	0,148	0,181	0,202	0,239	0,148	0,145	0,076
20	0,149	0,140	0,174	0,205	0,231	0,137	0,137	0,077
25	0,145	0,133	0,168	0,199	0,224	0,129	0,133	0,079
30	0,139	0,127	0,162	0,194	0,217	0,121	0,130	0,080
35	-	0,122	0,157	0,189	0,210	0,117	0,128	0,082
40	-	0,118	0,153	0,185	0,205	0,113	0,126	0,084
45	-	0,114	0,148	0,181	0,199	0,109	0,124	0,086
50	-	0,111	0,145	0,178	0,194	0,106	0,123	0,085
55	-	0,108	0,142	0,174	0,189	0,106	0,120	-
60	-	0,106	0,140	0,171	0,185	0,106	0,119	0,087
65	-	0,104	0,138	0,168	0,181	0,106	0,118	-
70	-	0,102	0,136	0,165	0,177	0,106	0,117	0,090
75	-	0,101	0,133	0,163	0,174	-	0,116	-

Во втором случае используется уравнение (II-365). Параметры этого уравнения для наиболее распространенных в поверхностных водах газовых компонентов представлены в Таблице II-35.

Рисунок II-3. Константы уравнения Рея Вайса (II-365) для определения величин коэффициента растворимости Бунзена в мл·л^-1атм^-1.

Газовые компоненты	Коэфф. Бунзена (T=25oC, pi=1 атм, mв=0‰)	Константы уравнения (II-360)						Стандартная ошибка		Источник
		A1	A2	A3	B1	B2	B3
N2	14,8	-52,7196	85,7661	24,3696	-0,05158	0,026329	-0,0037252		-		Weiss R. F., 1970
O2	28,2	-51,4797	85,8079	23,8439	-0,034892	0,015568	-0,0019387		-		Weiss R. F., 1970
CH4	30,1	-61,9782	101,4956	28,7314	-0,076146	0,04397	-0,0068672		±0,5%		Wiesenburg D.A., et al., 1979
CO2	757	-48,0757	90,5069	22,294	0,027766	-0,025888	0,0050578		±0,2%		Weiss R. F., 1974
CO	21,4	-40,7068	69,5068	18,7397	0,045657	-0,040721	0,00797		±0,4%		Wiesenburg D.A., et al., 1979
H2	17,5	-40,9868	65,0368	20,1709	-0,82225	0,049564	-0,0078689		±0,46%		Wiesenburg D.A., et al., 1979
Ar	30,6	-48,7498	82,0262	22,5929	0,036267	0,016241	-0,0020114		-		Weiss R. F., 1970
Ne	12,2	-32,2891	51,8013	15,7699	-0,124695	0,078374	-0,0127972		±0,3%		Weiss R. F., 1971
He	8,5	-27,7181	43,0285	14,1391	-0,042340	0,022624	-0,0033120		±0,3%		Weiss R. F., 1971

На глубинах, где пластовое давление заметно выше 1 атм, необходимо учитывать взаимодействие компонентов подземного газа между собой. Группа Женхуа Дуана комбинируя уравнение К.С. Питцера (II-366) и уравнения состояния реального газового раствора рассчитала коэффициенты Бунзена для O₂, N₂, CH₄, H₂S и CO₂ в условиях температуры от 0 до 200-300^oC, давления от 1 до 200-2000 бар и минерализации воды от 0 до 6 моль·кг^-1 NaCl (Duan Z., Mao S., 2006; Duan Z., Sunc R., 2003; Duan Z., SunR., Liu R., Zhu C., 2007; Mao S., Duan Z., 2006; Geng M., Duan Z., 2010 ).

Однако, при использовании коэффициентов растворимости не учитывается влияние растворенных летучих компонентов. Чтобы учесть влияние летучих на растворимость друг друга в воде воспользуемся давлением насыщения. В момент, когда давление насыщения достигнуто в воде появляется ничтожная по объему газовая фаза. Для неё справедливо равенство II-370. В то же время для воды справедливо равенство II-359. В случае равновесия справедливо равенство II-378, и поэтому:

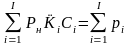(II‑4)

Тогда, согласно уравнениям II-351 и II-368, имеем два равенства:

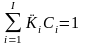и . (II‑5)

Так как в этом случае P_н =P, величины коэффициентов распределения определяются как функция давления насыщения, температуры и минерализации. Если давление насыщения известно, то величина коэффициента распределения подбирается непосредственно по его величине. Если давление насыщения не известно, его величина определяется путем подбора при заданной температуре и минерализации таких коэффициентов распределения, при которых соблюдается первое равенство в II-381. При этом предварительно учитывается влияние минерализации по уравнению:

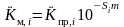. (II‑6)

где S_i - коэффициент Савченко.

Пример II‑1.

Необходимо определить парциальные давления газовых компонентов с помощью коэффициентов растворимости Бунзена, если их концентрации имеют значения, показанные в строке 1 таблицы. Минерализация воды 118 г/л, плотность 1,08 г/мл, температура +40^oС.

Величины коэффициентов растворимости Бунзена (строка 2) и коэффициентов Сеченова (строка 3) для температуры 40^o С подбираются в справочной литературе или приложениях. При использовании коэффициента Сеченова минерализация выражается числом молей NaCl, поэтому m =118/58 =2,03 моль/л. Рассчитываем коэффициенты Бунзена с учетом влияния минерализации (строка 4):

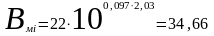мл∙л^-1∙ат^-1.

Парциальное давление каждого компонента равно отношению его концентрации к величине исправленного коэффициента растворимости Бунзена. В случае метана p_CH4=510/34,66=14,7 ат.

№	Компоненты	CH4	C2H6	N2	Ar	He
1	Объемное содержание, мл/л	510	12	72	3	3
2	Коэффициент растворимости Бунзена, мл∙л-1∙ат-1	22	17,4	11	25,2	8,8
3	Коэффициент Сеченова	0,097	0,087	0,11	0,126	0,084
4	С поправкой Сеченова, мл∙л-1∙ат-1	34,7	26,2	18,4	45,5	13,0
6	Парциальное давление, ат	14,7	0,46	3,91	0,066	0,23

Пример II‑21.

Согласно примерам, рассмотренным выше, подземная вода содержат мольные доли газовых компонентов, показанные в столбце 4 таблицы ниже. Необходимо определить их парциальные давления, если минерализация воды 156,6 г/л, плотность 1,08 г/мл и температура +100^o С.

Для решения поставленной задачи необходимо прежде всего подобрать коэффициенты распределения для пресных вод, величина которых зависит только от температуры и давления насыщения. Температура известна, а давление насыщения нет. Следовательно, надо подбирать коэффициент распределения, как функцию давления насыщения при заданной температуре. Ориентировочную оценку величины давления насыщения дает парциальное давление преобладающего газового компонента, рассчитанное по коэффициенту растворимости. Согласно данным предыдущей задачи давление насыщения может быть больше 14,7 атм. Коэффициенты распределения этого давления и константы будут равны: для метана, для азота, для этана, для аргона, для гелия 3230. Используя формулу и коэффициенты Савченко, рассчитаем константы равновесия для воды с минерализацией 118 г/л, т.е. приблизительно 2 г-экв/л. Исправленные константы равновесия будут равны: для метана 2550, для азота 4460, для этана 3140, для аргона, для гелия 4750. Подставляем полученные значения в уравнение равновесия и получаем 1,4016. Так как полученная величина больше 1, задаемся новым более высоким давлением 5,0 МПа. Операции продолжаются до тех пор, пока сумма главного уравнения не станет равной 1. В нашем примере это достигается при давлении равном 5,6 МПа. Это означает, что газовые компоненты исследуемой воды начнут образовывать подземный газ при давлении 5,6 МПа. Содержание каждого компонента в этом газе равняется соответствующему слагаемому решаемого уравнения, т.е. произведению константы равновесия на мольную долю газового компонента в воде:

и .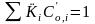

Тогда парциальное давление газовых компонентов, как в равновесном подземном газе, так и в подземной воде будет равняться произведению водном растворе будет равно произведению давления насыщения на мольную долю газового компонента в составе равновесного подземного газа:

.

№ п/п	Компоненты	CH4	C2H6	N2	Ar	He
1	Мольные доли, ‰	0,426	0,01	0,06	0,0025	0,0025
2	4МПа, прес.	1480	1550	2650	1020	3230
3	4МПа, 2 г-экв/л	2550	3140	4460	1820	4750	1,4016
4	5 МПа, 2 г-экв/л
5
6
7

. Решение задачи

Компоненты	Состав пробы природного газа, мольные %	Состав той же пробы без компонентов воздуха, мольные %	Содержание газовых компонентов в воде		I. Коэффициенты распределения при давлении насыщения 15 МПа		Состав равновесного подземного газа при пластовом давлении 15 МПа, в мольных долях	II. Коэффициенты распределения при давлении насыщения 20 МПа		Состав равновесного подземного газа при пластовом давлении 20 МПа, в мольных долях	III. Коэффициенты распределения при давлении насыщения 25 МПа		Состав равновесного подземного газа при пластовом давлении 25 МПа, в мольных долях		Парциальные давления газовых компонентов при давлении насыщения 25 МПа, в МПа
			в мл/л	в мольных долях	в пресной воде	в минерализованной воде		в пресной воде	в минерализованной воде		в пресной воде	в минерализованной воде
1	2	3	4	5	6	7	8	9	10	11	12	13		14		15
He	0,09	0,095	1,08	8,64·10-07	800	1445,7	0,0012	540	975,8	0,00084	455	822,2		0,00071		0,018
Ar	0,037	0,037	0,42	3,39·10-07	523	1127,9	0,00038	412	888,6	0,00030	365	787,2		0,00027		0,0067
O2	0,5	0	0	0		0	0		0	0		0		0		0
N2	11,3	9,94	112,80	9,05·10-05	880	2214,2	0,20	680	1711,0	0,15	570	1434,2		0,13		3,25
CO2	1	1,05	11,94	9,59·10-06	54,6	95,7	0,00092	48,5	85,0	0,00081	47,7	83,6		0,00080		0,020
CH4	79,1	83,30	945,52	75,89·10-05	589	1189,3	0,90	466	940,91	0,71	397	801,6		0,61		15,21
C2H6	3,4	3,58	40,64	3,26·10-05	1078	2458,6	0,080	1007	2295,8	0,075	933	2127,1		0,069		1,73
C3H8	0,41	0,43	4,90	3,93·10-06	3089	8537,0	0,034	2970	8206,9	0,032	2883	7966,5		0,031		0,78
C4H10	1,48	1,56	17,69	1,42·10-05	7352	21237,2	1,22	7260	20971,8	0,30	7170	20711,8		0,29		7,35
Сумма	97,317	100	1135	91,10·10-06			2,44			1,28				1,13		28,37
NaCl				0,048160723
H2O				0,950928245