Раздел 1.

Точка, прямая, плоскость и их взаиморасположение.

Тема 1. Точка.

Упражнение 1.

Задача 1. По данным координатам точки А (4; 3; 6) постройте косоугольную изометрию (рис.1а) и ортогональные проекции (рис 1б) этой точки (4 – координата точки А по оси OХ; 3 – по оси OY; 6 - по оси OZ).

Задача 2. Постройте недостающие проекции точки А, расположенной в I, II, III, IV четвертях пространства.

Тема 2. Точка в различных четвертях (октантах).

Упражнение 2.

Задача 1. Постройте проекции точек, заданных координатами из табл. 1.2. Каждую точку задайте двумя проекциями.

Точки	x	y	z
A	1	4	3
B	2	-2	4
C	3	-3	-1
D	4	4	-5
E	5	4	4
F	6	-3	3
G	7	-2	-2
J	8	5	-5
K	9	-4	0
L	10	0	-3
M	11	0	0

Задача 2. Постройте недостающие проекции точек C, D и E.

Тема 3. Прямая линия.

Упражнение 3.

Следы прямой линии.

Следом прямой называется точка, в которой прямая пересекается с плоскостью проекций ( N – фронтальный след, М – горизонтальный).

Задача 1 а, б. Постройте косоугольно – изометрический чертеж 1а) и эпюр (1б) отрезка прямой АВ: А (3,1,8); В (10,7,1). По эпюру отрезка определите: а) истинную длину отрезка – на плоскостях Н и V по способу прямоугольной трапеции, а на плоскостях W – по способу прямоугольного треугольника; б) углы наклона α, β, γ к плоскостям Н, V, W; в) следы М и N на плоскостях Н и V.

1а) 1б)

На косоугольно – изометрическом чертеже постройте следы М и N и обозначьте Н.В. отрезка АВ и углы наклона α, β, γ к плоскостям проекций.

Задача 2. Постройте следы прямых АВ и CD и определите Н.В. этих прямых.

Тема 4. Плоскость.

Упражнение 4.

Задача 1. Постройте следы плоскости, заданной треугольником АВС.

Задача 2. Достройте горизонтальную проекцию треугольника АВС, лежащего в плоскости Р.

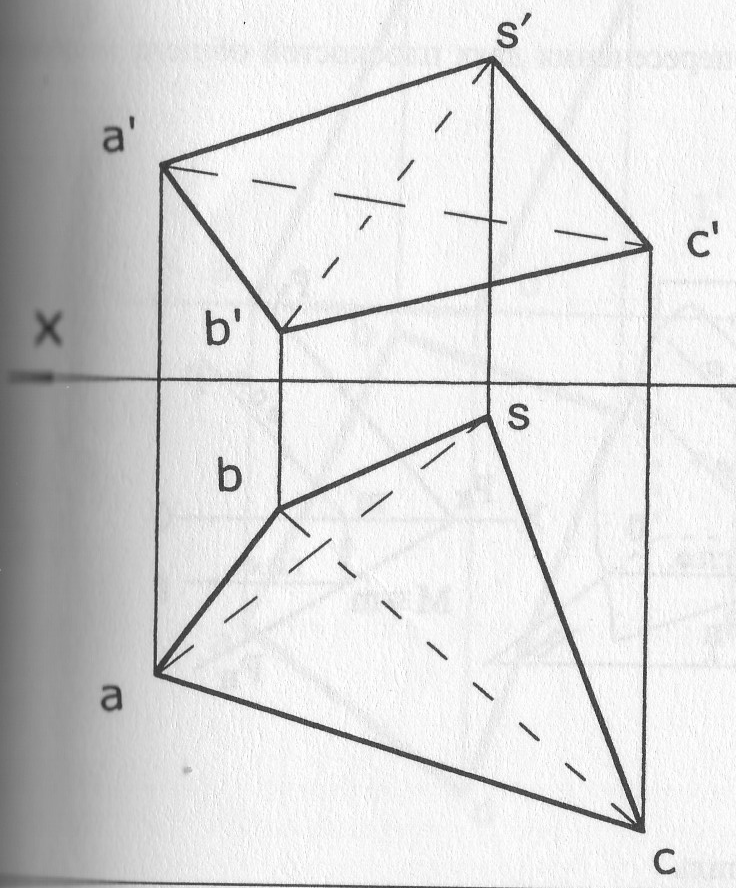
Задача 3. Определите видимость ребер пирамиды SABC.

Задача 4. Через прямые EF проведите следующие плоскости:

а) плоскость Р – горизонтально проецирующую;

б) плоскость Q – фронтально проецирующую;

в) плоскость R – профильно проецирующую.

Указанные плоскости изобразите двумя пересекающимися прямыми и следами.

Задача 5. Через точку Е проведите отрезок прямой ЕF произвольной длины, параллельный отрезку АВ, и определите расстояние между ними.