Двоичная запись цифровых данных

Унарная система чрезвычайно неэф­фективна для записи больших чисел. Поэто­му мы по большей части будем использовать вышеописанную двоичную систему. Однако, сделать это напрямую и попытаться читать ленту просто как двоичное число мы не смо­жем. Дело в том, что мы не имеем возможно­сти сказать, когда кончается двоичное пред­ставление числа и начинается бесконечная последовательность нулей справа, которая отвечает пустой ленте. Нам нужен способ как-то обозначать конец двоичной записи числа. Более того, часто нам будет нуж­но вводить в машину несколько чисел, как, например, в случае с алгоритмом Евклида, когда требуется пара чисел '²'. Но в двоич­ном представлении мы не можем отличить пробелы между числами от нулей или стро­чек нулей, входящих в записи этих двоич­ных чисел. К тому же, помимо чисел нам может понадобиться и запись всевозмож­ных сложных инструкций на той же ленте. Для того чтобы преодолеть эти трудности, воспользуемся процедурой, которую я буду в дальнейшем называть сокращением и со­гласно которой любая строчка нулей и еди­ниц (с конечным числом единиц) не просто считывается как двоичное число, но заме­щается строкой из нулей, единиц, двоек, троек и т.д. таким образом, чтобы каждое число в получившейся строчке соответство­вало числу единиц между соседними нулями в исходной записи двоичного числа. Напри­мер, последовательность:

превратиться в

Мы теперь можем считывать числа 2, 3, 4, ... как метки или инструкции опреде­ленного рода. Действительно, пусть 2 будет просто «запятой», указывающей на пробел между двумя числами, а числа 3, 4, 5, ... могли бы по нашему желанию символизиро­вать различные инструкции или необходи­мые обозначения, как, например, «минус», «плюс», «умножить», «перейти в позицию со следующим числом», «повторить пре­дыдущую операцию следующее число раз» и т.п. Теперь у нас есть разнообразные по­следовательности нулей и единиц, разде­ленные цифрами большей величины. Эти последовательности нулей и единиц будут представлять собой обычные числа, запи­санные в двоичной форме. Тогда записанная выше строка (при замене двоек «запятыми») примет вид:

Используя обычные арабские числа «9», «3», «4», «О» для записи соответствующих двоич­ных чисел 1001, 11, 100 и 0, получаем но­вую запись всей последовательности в виде:

Такая процедура дает нам, в частно­сти, возможность указывать, где заканчива­ется запись числа (и тем самым отделять ее от бесконечной полосы пустой ленты спра­ва), просто используя запятую в конце этой записи. Более того, она позволяет закоди­ровать любую последовательность натураль­ных чисел, записанных в двоичной систе­ме, как простую последовательность нулей и единиц, в которой для разделения чисел мы используем запятые. Посмотрим, как это сделать, на конкретном примере. Возьмем последовательность:

В двоичном представлении она эквивалент­на последовательности

что на ленте можно записать с помощью операции расширения (обратной по отноше­нию к описанной выше процедуре сокраще­ния) как

Такое кодирование легко выполнить, если в исходной двоичной записи чисел про­вести следующие замены:

и после этого добавить бесконечные после­довательности нулей с обеих сторон вновь полученной записи. Чтобы сделать более по­нятной эту процедуру в применении к наше­му примеру, разделим полученные двоичные числа пробелами:

Я буду называть этот способ представле­ния (наборов) чисел расширенной двоичной записью. (Так, в частности, в расширенной двоичной форме записи число 13 выглядит как 1010010.)

Есть еще одно, последнее, замечание, которое надо сделать в связи с этой систе­мой записи. Это не более, чем техничес­кая деталь, но она необходима для полно­ты изложения. Двоичная (или десятич­ная) запись натуральных чисел в некоторой степени избыточна в том смысле, что ну­ли, расположенные слева от записи числа, «не считаются» и обычно опускаются, так что 00110010 представляет собой то же са­мое двоичное число, что и 110010 (а 0050 — то же самое десятичное число, что и 50). Эта избыточность распространяется и на нуль, который может быть записан и как 000, и как 00, и, конечно, как 0. На самом деле и пустое поле, если рассуждать логически, должно обозначать нуль! В обычном пред­ставлении это привело бы к большой пута­нице, но в описанной выше системе коди­рования никаких затруднений не возникает: нуль между двумя запятыми можно запи­сать просто в виде двух запятых, следующих подряд (,,). На ленте такой записи будет со­ответствовать код, состоящий из двух пар единиц, разделенных одним нулем:

Тогда исходный набор из шести чисел может быть записан в двоичной форме как

и на ленте при кодировании в расширен­ной двоичной форме мы получим последо­вательность

в которой на один нуль меньше по сравне­нию с предыдущим кодом того же набора.

Теперь мы можем рассмотреть машину Тьюринга, реализующую, скажем, алгоритм Евклида в применении к паре чисел, за­писанных в расширенной бинарной форме. Для примера возьмем ту же пару чисел — 6 и 8, которую мы брали ранее. Вместо преж­ней унарной записи

воспользуемся двоичным представлением 6 и 8, т.е. ПО и 1000, соответственно. Тогда эта пара имеет вид: 6, 8, или в двоичной форме 110, 1000, и в расширенной двоичной записи на ленте она будет выглядеть следующим образом

Для этой конкретной пары чисел двоичная форма записи не дает никакого выигрыша по сравнению с унарной. Предположим, од­нако, что мы берем для вычислений (деся­тичные) числа 1 583 169 и 8610. В двоичной записи они имеют вид

На ленте при расширенном двоичном коди­ровании им будет соответствовать последо­вательность

которая занимает менее двух строк, тогда как для унарной записи пары чисел «1 583 169, 8610» не хватило бы места на страницах этой книги!

Машину Тьюринга, выполняющую ал­горитм Евклида для чисел, записанных в расширенной двоичной форме, при жела­нии можно получить из EUC с помощью пары дополнительных алгоритмов, которые переводили бы числа из расширенной дво­ичной формы в унарную и обратно. Однако, такой подход чрезвычайно неэффективен, ибо громоздкость унарной системы записи была бы по-прежнему «внутренне» прису­ща всему устройству, что проявилось бы в его низком быстродействии и потребно­сти в огромном количестве «черновиков» (на левой стороне ленты). Можно постро­ить и более эффективную машину Тьюрин­га для алгоритма Евклида, оперирующуюисключительно расширенными двоичными числами, но для понимания принципов ее работы это не особенно важно.

Для того чтобы показать, каким обра­зом машина Тьюринга может работать с чи­слами в расширенном двоичном представле­нии, обратимся к значительно более про­стой, чем алгоритм Евклида, процедуре -просто прибавлению единицы к произвольно­му натуральному числу. Ее можно выпол­нить с помощью следующей машины Тью­ринга (которую я назову XN + 1):

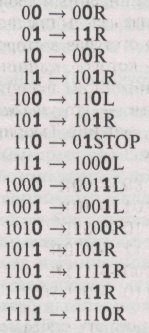
И вновь некоторые дотошные читатели могут захотеть проверить, вправду ли эта ма­шина Тьюринга действует так, как должна, если взять, скажем, число 167. Это чис­ло имеет двоичное представление 10100111 и записывается на ленте как

Чтобы прибавить единицу к двоичному чис­лу, мы просто находим в его записи по­следний нуль и меняем его на единицу, а все непосредственно следующие за ним единицы — на нули. Так что 167 + 1 = 168 в двоичной форме записывается в виде

Таким образом, наша «прибавляющая еди­ницу» машина Тьюринга должна превратить предыдущую запись на ленте в

что она и делает.

Обратите внимание, что даже самая простая операция прибавления единицы в такой записи выглядит довольно сложно, включая в себя 15 инструкций и восемь различных внутренних состояний! Конечно, в случае унарной записи все было значи­тельно проще, поскольку тогда «прибавле­ние единицы» означало удлинение строчки единиц еще на одну, поэтому не удивитель­но, что машина UN+ 1 была более простой. Однако, для очень больших чисел UN + 1 была бы слишком медленной из-за чрез­мерной длины ленты, и тогда более сложная машина XN + 1, но работающая с более компактным расширенным двоичным пред­ставлением, оказалась бы предпочтительнее. Несколько отступая в сторону, я укажу операцию, для которой машина Тьюринга проще в расширенной двоичной, нежели в унарной форме — это умножение на два. Действительно, машина Тьюринга XN x 2, заданная в виде:

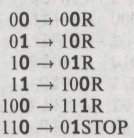
запросто выполнит эту операцию в расши­ренной двоичной форме, тогда как соответ­ствующая унарная машина UN x 2, описан­ная ранее, гораздо сложнее!

Этот раздел дает определенное предста­вление о том, на что способны в простейших случаях машины Тьюринга. Как и следовало ожидать, при выполнении более или менее сложных операций эти машины могут стано­виться, и действительно становятся, несрав­ненно более сложными. Каковы же прин­ципиальные возможности таких устройств? Мы рассмотрим этот вопрос в следующем параграфе.