Вариант 15

1. Прибор работает в двух режимах: в нормальном и в условиях перегрузки. Нормальный режим осуществляется в 80% времени, условия перегрузки – в 20%. Вероятность выхода прибора из строя равна 0,1 в нормальных условиях и 0,6 в условиях перегрузки. Найти вероятность выхода прибора из строя при произвольном режиме.

2. Решить предыдущую задачу при условии, что прибор вышел из строя. Найти вероятность того, что это произошло в условиях перегрузки.

3. В партии 10% нестандартных деталей. Найти вероятность того, что среди четырех отобранных деталей две нестандартные.

4. Вероятность появления события в каждом из 100 испытаний равна 0,2. Найти вероятность того, что событие появится не менее 75 раз.

Задание III.

1. Найти закон распределения случайной величины X. Вычислить M(X) и D(X). Найти функцию распределения F(x) д.с.в. X и построить ее график.

2. Дискретная случайная величина X может принимать только два возможных значения и , причем 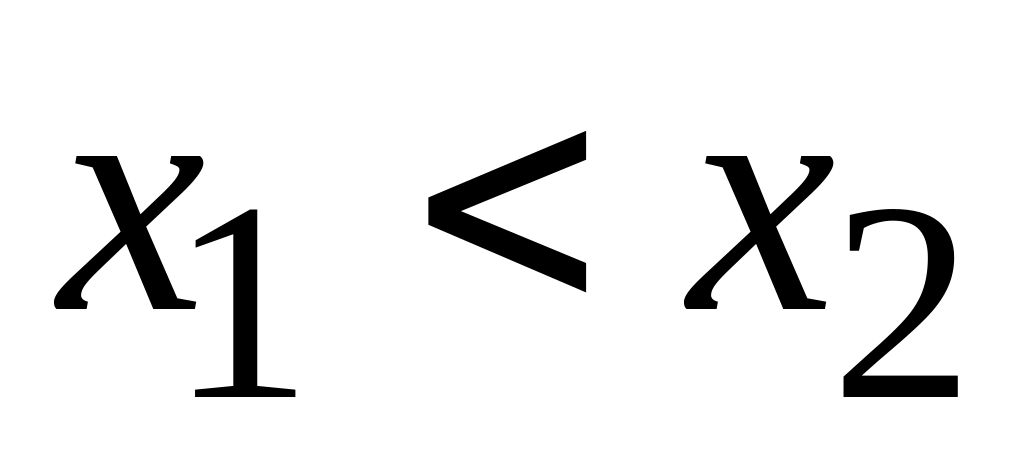. Известны вероятность возможного значения , математическое ожидание M(X) и дисперсия D(X). Найти закон распределения случайной величины.

3. Непрерывная случайная величина X задана функцией распределения F(x). Найти плотность вероятности f(x), математическое ожидание M(X) и дисперсию D(X) непрерывной случайной величины . Построить графики функций f(x) и F(x).

4. Найти вероятность попадания случайной величины X в замкнутый интервал 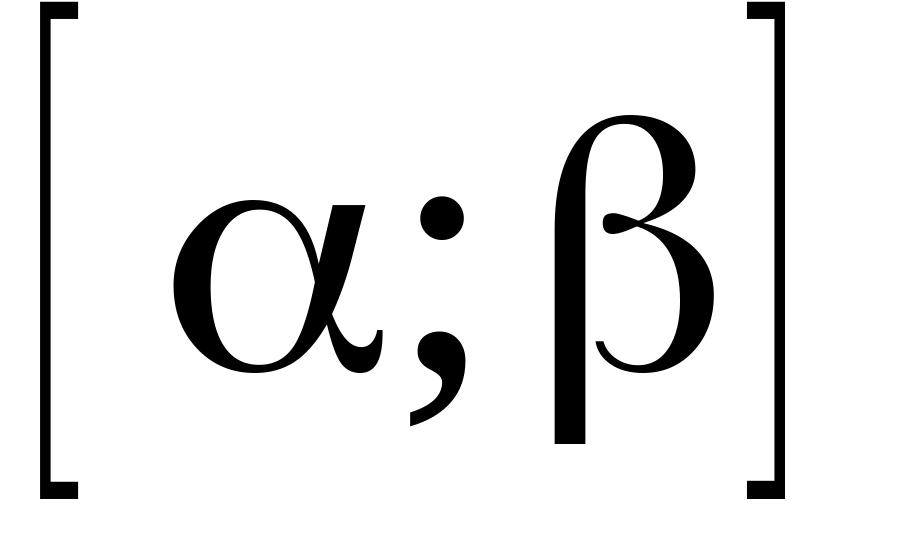, если она распределена:

1. равномерно на отрезке ;

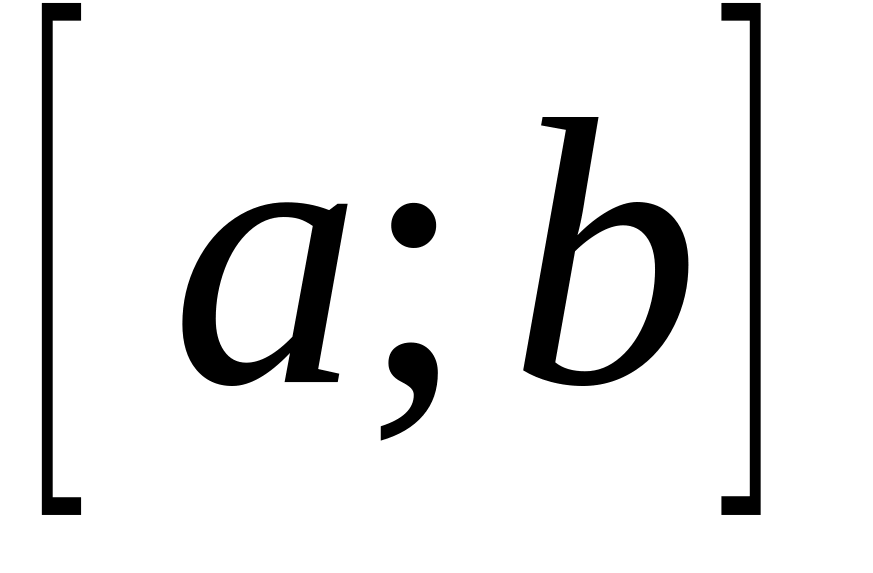2. по показательному закону и имеет математическое ожидание ;

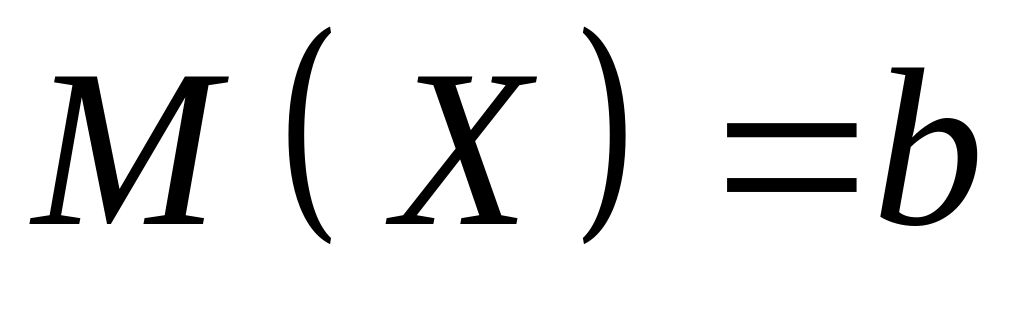3. по нормальному закону, при этом .

5. Решить задачу.

Вариант 1

1. Вероятности рождения мальчика и девочки предполагаются одинаковыми. X – число мальчиков в семье, имеющей пять детей.

2. 

3. 

4. 

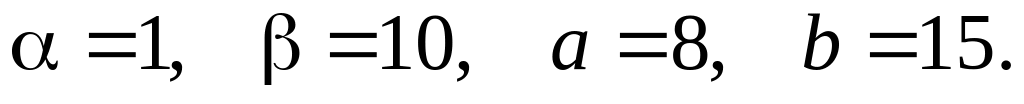
5. Срок службы прибора представляет собой случайную величину, имеющую нормальное распределение, с гарантией на 15 лет и с.к.о., равным 3 годам. Какова вероятность того, что три таких прибора прослужат от 10 до 20 лет?

Вариант 2

1. Охотник стреляет по дичи до первого попадания, но успевает сделать не более четырех выстрелов. Вероятность попадания в цель при одном выстреле равна 0,7. X – число выстрелов.

2. 

3. 

4. 

5. Вес мотка пряжи – случайная величина, имеющая нормальное распределение с математическим ожиданием 100 г. Найти ее дисперсию, если отклонение веса мотка от среднего, превышающее 10 г, происходит с вероятностью 0,05.

Вариант 3

1. Из урны, в которой 4 белых и 6 черных шаров, вынимают шары по одному без возврата до появления черного шара. X – число появлений белых шаров.

2. 

3. 

4. 

5. Процент содержания крахмала в картофеле является нормально распределенной случайной величиной с математическим ожиданием 18% и с.к.о. 3%. Какова вероятность того, что обе наудачу взятые картофелины содержат от 16% до 22% крахмала?

Вариант 4

1. В урне находятся 3 белых и 2 черных шара. Шары извлекают по одному без возврата до появления черного шара. X – число извлеченных шаров.

2. 

3. 

4. 

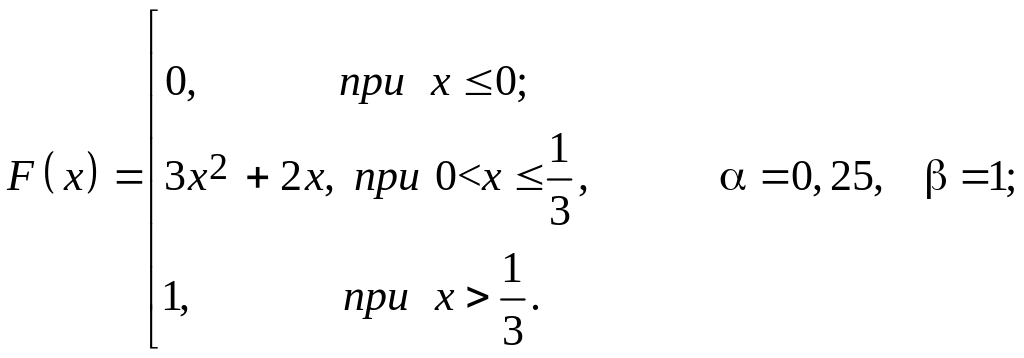
5. Размер детали подчинен нормальному закону с параметрами = 30 микрон и  = 5 микрон. Детали считаются годными, если их размер находится в пределах от 20 до 40 микрон. Если размер детали больше 40 микрон, она подлежит переделке. Каково число деталей, подлежащих переделке, из произведенных 1000 деталей?