1.3 Статические и динамические модели

Другим принципом классификации целей моделирования может служить деление моделей на статические и динамические.

По признаку учета зависимости объекта моделирования от времени различают статические и динамические характеристики систем, отражаемые в соответствующих моделях.

Статические модели (модели статики) отражают функцию системы - конкретное состояние реальной или проектируемой системы (своего рода его «мгновенную фотографию»)

Примеры. Закон Ома, описание показателей эффективности организацией в некоторый момент времени.

Динамические модели (модели динамики) отражают функционирование системы - процесс изменения состояний реальной или проектируемой системы. Они показывают различия между состояниями, последовательность смены состояний и развитие событий с течением времени.

Примеры. Описание процесса изменения спроса на какой-либо товар под влиянием рекламы, изменение температуры электроплиты при ее включении, описание процесса изменения показателей эффективности за некоторый период времени.

Отличие статических и динамических моделей заключено в учете времени: в статике его как бы не существует, а в динамике это основной элемент.

Статические характеристики систем.

В узком смысле к статической характеристике системы можно отнести ее структуру. Однако нас чаще будут интересовать свойства системы по преобразованию ходов и выходов (т.е. функция системы) в установившемся режиме, когда отсутствуют изменения значений как входных, так и выходных переменных. Такие свойства определяются как статические характеристики.

Статическая характеристика - это зависимость между входной и выходной величинами в установившемся режиме. Статическая характеристика может быть представлена:

• математической моделью вида Y = F(X)

• графической моделью.

Динамические характеристики систем

Следующий шаг в исследовании систем состоит в том, чтобы понять и описать, как система «работает», что происходит с ней самой и с окружающей средой в ходе реализации поставленной цели. Для описаний функционирования системы используются динамические модели.

Динамическая характеристика - это реакция системы на возмущение (зависимость изменения выходных переменных входных и от времени).

Динамическая характеристика может быть представлена:

• математической моделью в виде дифференциального уравнения (или уравнений) вида:

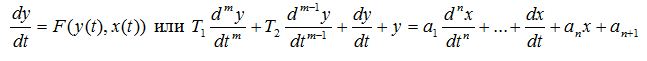
• математической моделью в виде решения дифференциального уравнения;

• графической моделью, состоящей из двух графиков: графика изменения возмущения во времени и графика реакции выхода на это возмущение - графической зависимости изменения выхода во времени.

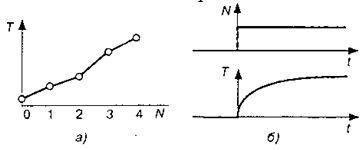
Рисунок 3- Статическая (а) и динамическая (б) характеристики электроплиты

При исследовании динамики систем часто невозможно составить математическое описание всей системы сразу. Для отображения динамических свойств элементов системы независимо от их физической природы используют понятие динамического звена.

Динамическое звено - это часть системы или элемента, описываемая определенным дифференциальным уравнением. Динамическим звеном можно представить элемент, совокупность элементов, автоматическую систему в целом.

Любую динамическую систему можно условно разложить на динамические «атомы» - элементарные динамические звенья. Упрощенно элементарным динамическим звеном можно считать звено с одним входом и одним выходом

Рисунок 4 - Элементарное динамическое звено.

Математическое описание всей системы в целом может быть получено как совокупность независимых друг от друга уравнений или характеристик отдельных звеньев, образующих систему, дополненных уравнениями связи между звеньями.

Дифференциальные уравнения элементов имеют порядок не выше второго, поэтому типовые звенья описываются дифференциальными уравнениями нулевого, первого и второго порядка. При математическом моделирований некоторого процесса его конкретная реализация описывается в виде соответствия между элементами множества Х возможных “значений” х и элементов упорядоченного множества Т “моментов времени” t, т.е. в виде отображения TX: x(t)  X^T, tT. С помощью этих понятий можно строить математические модели систем.

Рисунок 5 - Элементарное динамическое звено. (зависимость от времени)

Статическое моделирование служит для описания состояния объекта в фиксированный момент времени, а динамическое — для исследования объекта во времени. При этом оперируют аналоговыми (непрерывными), дискретными и смешанными моделями.