5.4.3. Пример разложения в комплексный ряд Фурье
В качестве примера попробуем разложить в ряд Фурье прямоугольный сигнал с периодом T, изображенный на Рис. 5.14. Коэффициенты Фурье выражаются следующим образом:
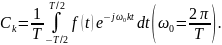
Но
поскольку функция f(t)
при
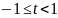равна 1, а в остальных случаях она равна
0, то при
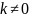
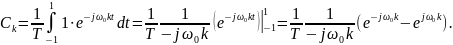
Исходя из формулы Эйлера
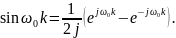
а значит,
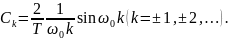
При k = 0
а)
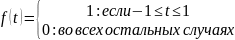
Последовательность
прямоугольных импульсов и ее спектр
Функция
f(t)
– четная, поэтому коэффициенты Фурье
состоят только из действительных частей
б)
Функция
выборочного значения
Действительные
части коэффициентов Фурье
в)
При
Т
= 8
Рис. 5.14. Последовательность прямоугольных импульсов и ее спектр
Понятно,
что коэффициенты Ck
являются
действительными числами. Это также ясно
и из того, что f(t)
– четная функция. Величина фазы при
положительном значении Ck
равна 0. Если Ck
принимает отрицательные значения, то
величина фазы равна
.
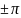Функцию
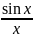
можно
представить графически, как показано
на Рис.
5.14б.
Эта функция называется функцией
выборки (единичного
отсчета). Если считать, ч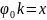то
,
то
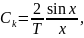
т.е. коэффициенты Ck принимают вид, подобный функции выборки.
Попробуем изобразить графически коэффициенты Фурье. Пусть значение k отложено по оси абсцисс, а Re(Ck) – по оси ординат. На Рис.5.14в в качестве примера представлен спектр последовательности прямоугольных импульсов при T = 8.
1 Вишневский В.М., Портной С.Л., Шахнович И.В. Энциклопедия WiMax. Путь к 4G. М.: Техносфера, 2009. – 472 с.
2 Сато Юкио. Обработка сигналов. Первое знакомство / Под ред. Есифуми Амэмия, М.:Додека, 2002. – 175 с.
3 Харкевич А.А. Теоретические основы радиосвязи. М.: Гос. из-во технико-теоретической литературы, 1957. – 347 с.
4 Харкевич А.А. Теоретические основы радиосвязи. М.: Гос. из-во технико-теоретической литературы, 1957. – 347 с.
5 Сато Юкио. Обработка сигналов. Первое знакомство / Под ред. Есифуми Амэмия, М.:Додека, 2002. – 175 с.