3.5 Переход от векторного пространства к пространству функций:

Мы уже знаем, как выразить скалярное произведение и расстояние между векторами в двумерном пространстве. А как быть в случае пространства большего числа измерений. Рассмотрим, например, вектор трехмерного пространства:

f =(f_1, f_2, f₃)

Известно, что его норму или расстояние от исходной точки до точки

(f_1,f_2,f₃) можно выразить как:

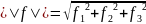(3.10)

Обобщая выражение (3.10), можно предположить, что норма вектора

f =( f_1,f_2,……,f_N) N- мерного пространства определяется как:

(3.11)

А как же будет выглядеть норма вектора в случае пространства бесконечной размерности, иначе говоря, пространства функций. Норма функции ʃ(t) в этом случае является величиной функции. Каким же образом её определять? Это становится понятным, если обратиться к формуле, которая часто используется применительно к физическим явлениям(см. памятку ниже).

Норма функции f(t) (а≤t≤b) определяется соотношением:

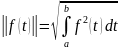
Как обобщение N-векторной нормы. Это определение, в общем, нас устраивает. Но чем больше интервал в этой формуле, тем больше значение нормы. Поэтому удобнее пронормировать норму функции f(t) относительно длины интервала

(3.12)

3.6. Система ортонормированных функций:

Мы уже знаем, как выразить вектор f двумерного пространства через ортонормированный базис векторов (V_1,V₂):

f = С₁v₁+C₂v₂

Таким же образом через ортонормированный базис можно выразить и в N-мерном пространстве (На рис.3.9 показан ортонормированный вектор в трехмерном пространстве).

Рис. 3.9 - Выражение вектора 3-мерного пространства через ортонормированный базис

Ортонормированный базис – это множество взаимно перпендикулярных единичных векторов. Множество векторов (V_k, k=1,2,….N) в N-мерном пространстве, где:

(т.е. V_m и V_n взаимно перпендикулярны и являются единичными), называется ортонормированным базисом N-мерного пространства. Для их выражения используется символ Кронекера δ_mn:

И в упрощённом виде записывается следующим образом:

(V_m, V_n)=δ_mn

Если все векторы взаимно перпендикулярны, то ни один из них нельзя выразить через другие векторы. Иначе, говоря, они независимы.

Используя ортонормированный базис векторов, можно представить вектор в виде линейной комбинации базисных векторов, можно представить вектор в виде линейной комбинации базисных векторов. Иначе говоря, N-мерный вектор можно представить в виде:

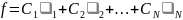
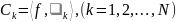
Пример

Образует ли система функций 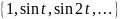на отрезке систему ортонормированных функций?

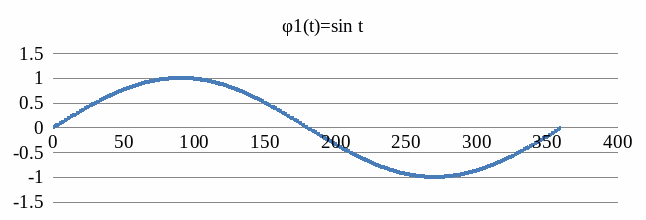
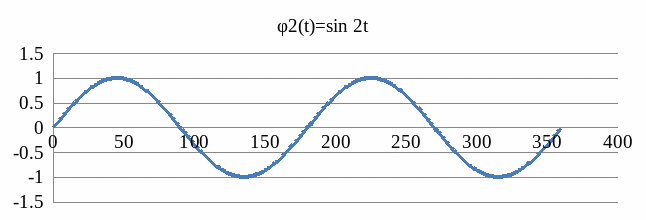
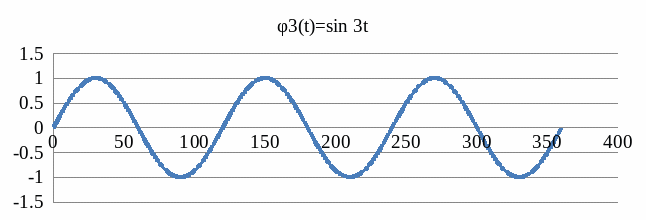
Следовательно, 1 и 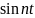взаимно перпендикулярны.

Если 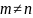, то

Следовательно, 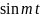и 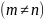также взаимно перпендикулярны.

Шпаргалка

Формулы разложения произведения тригонометрических функций на сумму

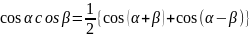
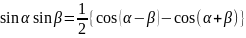
Из вышеизложенных результатов ясно, что множество функций образуют систему ортогональных функций. Однако норма каждой функции:

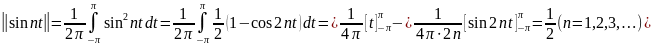
Шпаргалка

Формулы половинного угла

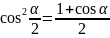
Норма каждой функции не равна 1, следовательно функции не являются ортонормированными

Если норма ||f(t)|| функции f(t) не равна 1, то создадим новую функцию f^*(t):

Очевидно, что норма f^*(t) равна 1. Подобная операция называется нормировкой системы функций. В нашем случае:

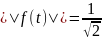
Поэтому, представляя исходную систему функций в новом виде:

(1, …).

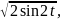Получим множество функций, образующих систему ортонормированных функций.

Обобщение:

1. Если для непрерывного сигнала f(t) произведена выборка из N значений, то этот сигнал можно представить в виде N-мерного вектора, который соответствует одной точке N-мерного пространства.

2. Величина сигнала выражается нормой вектора, а отличие двух сигналов - расстоянием между векторами. Скалярное произведение векторов - это произведение проекции одного вектора на длину другого. Коэффициент корреляции выражает угол между векторами, а также степень похожести сигналов. Чем больше по абсолютной величине коэффициент корреляции, тем более похожи сигналы. Если он равен 0, то векторы, отображающие сигналы, взаимно перпендикулярны.