5) Ортогональные проекции отрезка прямой общего положения. Прямые уровня и их проекции. Проецирующие прямые и их проекции.

Комплексный чертёж линии представляет собой совокупность проекций точек этой линии на две или три плоскости проекций. На комплексном чертеже необходимо установить связь между проекциями точек. В этом случае линия будет определена однозначно. По расположению относительно плоскостей проекций прямые могут быть общего и частного положений.  Прямой общего положения называется прямая, не параллельная ни одной из плоскостей проекций.

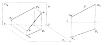
Прямые уровня - это прямые, принадлежащие плоскости и параллельные какай - либо плоскости проекций. Эти прямые называют прямыми уровня, так как они принадлежат плоскости уровня. Существует три вида прямых уровня:

Прямая h, параллельная горизонтальной плоскости проекций, называется горизонталью. На горизонтальную плоскость проекций горизонталь проецируется в натуральную величину.

Прямая уровня f, параллельная фронтальной плоскости проекций, называется фронталью. На фронтальную плоскость проекций фронталь проецируется в натуральную величину.

Профильная прямая p по отношению к профильной плоскости также является прямой уровня, поскольку параллельна ей. На профильную плоскость проекций профильная прямая проецируется в натуральную величину.

Прямая называется проецирующей, если она перпендикулярна одной из плоскостей проекций. Одна из проекций такой прямой есть точка. Эта проекция называется главной или вырожденной. Все точки проецирующей прямой являются конкурирующими.

1. Горизонтально проецирующая прямая - прямая   горизонтальной плоскости проекций. Горизонтальной проекцией такой прямой является точка, а фронтальная и профильная проекции || оси z.

2. Фронтально проецирующая прямая - прямая  фронтальной плоскости проекций. Фронтальной проекцией такой прямой является точка, а горизонтальная и профильная проекции || оси y.

3. Профильно проецирующая прямая - прямая  профильной плоскости проекций. Профильной проекцией такой прямой является точка, а горизонтальная и фронтальная проекции || оси x.

6) Следы прямой.

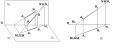
Точки пересечения прямой с плоскостями проекций называются следами прямой (рисунок 19)

.Следы прямой являются точками, одновременно принадлежащими как плоскости проекций, так и прямой. Фронтальная проекция фронтального следа и горизонтальная проекция горизонтального следа будут лежать в плоскостях проекций и совпадать с самим следом. Фронтальная проекция горизонтального следа и горизонтальная проекция фронтального следа будут лежать на оси проекций. Прямая, расположенная параллельно плоскости проекций, как находящаяся на всем своем протяжении на одинаковом расстоянии от плоскости, следа на ней не имеет.

7) Взаимное расположение точки и прямой. Взаимное расположение точки и плоскости.

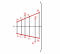
Если точка принадлежит прямой, то её проекции должны принадлежать одноименным проекциям этой прямой (аксиома принадлежности точки прямой).

Из четырех предложенных на рисунке точек, только одна точка С лежит на прямой АВ.

В тех случаях когда точка и прямая лежат в плоскости уровня (параллельной какой-либо из плоскостей проекций П₁, П₂ и П₃), то вопрос о взаимном расположении прямой и точки решается при построении проекций на плоскость соответственно П₁, П₂ или П₃. Например, прямая АВ и точка К лежат в плоскости параллельной профильной плоскости  проекций.

Возможны два варианта взаимного  расположения точки и плоскости: либо точка принадлежит плоскости, либо нет.

Если точка принадлежит плоскости то из трех проекций, определяющих положение точки в пространстве, произвольно задать можно только одну.