
- •22. Барометрическая формула. Распределение Больцмана.
- •24. Первый закон термодинамики
- •25. Второй закон термодинамики
- •100% Энергии не может быть преобразовано в работу
- •26. Третье начало термодинамики может быть сформулировано так:
- •27. Закон Кулона и напряженность электростатического поля.
- •28. Потенциал электростатического пoля.
- •29. Связь силовой и энергетической характеристик электрического поля.
- •30. Теорема Остроградского - Гаусса для поля в вакууме.
30. Теорема Остроградского - Гаусса для поля в вакууме.
Из
определения потока вектора напряженности
сквозь замкнутую поверхность, поток
вектора напряженности сквозь сферическую
поверхность радиуса r, которая охватывает
точечный заряд Q, находящийся в ее центре
(рис. 1), равен
![]() Этот
результат справедлив для замкнутой
поверхности произвольной формы.
Действительно, если заключить сферу
(рис. 1) в произвольную замкнутую
поверхность, то каждая линия напряженности,
которая пронизывает сферу, пройдет и
сквозь эту поверхность.
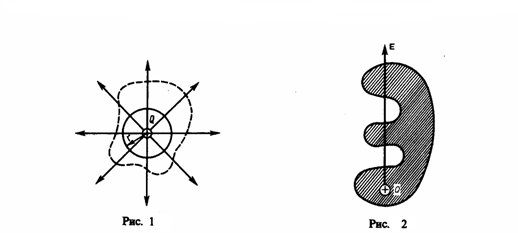
В случае,
если замкнутая поверхность любой формы
охватывает заряд (рис. 2), то при пересечении
любой линии напряженности с поверхностью
она то входит в нее, то выходит из нее.
При вычислении потока нечетное число
пересечений в конечном счете сводится
к одному пересечению, так как поток
полагается положительным, если линии
напряженности выходят из поверхности,
и отрицательным для линий, которые
входят в поверхность.
Этот
результат справедлив для замкнутой
поверхности произвольной формы.
Действительно, если заключить сферу
(рис. 1) в произвольную замкнутую
поверхность, то каждая линия напряженности,
которая пронизывает сферу, пройдет и
сквозь эту поверхность.
В случае,
если замкнутая поверхность любой формы
охватывает заряд (рис. 2), то при пересечении
любой линии напряженности с поверхностью
она то входит в нее, то выходит из нее.
При вычислении потока нечетное число
пересечений в конечном счете сводится
к одному пересечению, так как поток
полагается положительным, если линии
напряженности выходят из поверхности,
и отрицательным для линий, которые
входят в поверхность.
Если
замкнутая поверхность не охватывает
заряда, то поток сквозь нее равен нулю,
так как число линий напряженности,
которые входят в поверхность, равно
числу линий напряженности, которые
выходят из нее.
Значит, для
поверхности произвольной формы, если
она замкнута и заключает в себя точечный
заряд Q, поток вектора Е будет равен
Q/ε0, т. е.
![]() (1)
Знак
потока совпадает со знаком заряда
Q.
Исследуем общий случай
произвольной поверхности, окружающей
n зарядов. Используя с принцип суперпозиции,
напряженность Еполя, которая
создавается всеми зарядами, равна сумме
напряженностей Ei полей, которые
создаваются каждым зарядом в отдельности.
Поэтому
(1)
Знак
потока совпадает со знаком заряда
Q.
Исследуем общий случай
произвольной поверхности, окружающей
n зарядов. Используя с принцип суперпозиции,
напряженность Еполя, которая
создавается всеми зарядами, равна сумме
напряженностей Ei полей, которые
создаваются каждым зарядом в отдельности.
Поэтому
![]() Согласно
(1), каждый из интегралов, который стоит
под знаком суммы, равен Qi/ε0.
Значит,
Согласно
(1), каждый из интегралов, который стоит
под знаком суммы, равен Qi/ε0.
Значит,
![]() (2)
Формула
(2) выражает теорему Гаусса для
электростатического поля в вакууме:
поток вектора напряженности
электростатического поля в вакууме
сквозь произвольную замкнутую поверхность
равен алгебраической сумме заключенных
внутри этой поверхности зарядов, деленной
на ε0. Эта теорема получена математически
для векторного поля произвольной природы
русским математиком М.В.Остроградским
(1801—1862), а затем независимо от него
применительно к электростатическому
полю — К. Гауссом.
В общем
случае электрические заряды могут быть
распределены с некоторой объемной
плотностью ρ=dQ/dV, которая различна в
разных местах пространства. Тогда
суммарный заряд, заключенный внутри
замкнутой поверхности S, которая
охватывает некоторый объем
V,
(2)
Формула
(2) выражает теорему Гаусса для
электростатического поля в вакууме:
поток вектора напряженности
электростатического поля в вакууме
сквозь произвольную замкнутую поверхность
равен алгебраической сумме заключенных
внутри этой поверхности зарядов, деленной
на ε0. Эта теорема получена математически
для векторного поля произвольной природы
русским математиком М.В.Остроградским
(1801—1862), а затем независимо от него
применительно к электростатическому
полю — К. Гауссом.
В общем
случае электрические заряды могут быть
распределены с некоторой объемной
плотностью ρ=dQ/dV, которая различна в
разных местах пространства. Тогда
суммарный заряд, заключенный внутри
замкнутой поверхности S, которая
охватывает некоторый объем
V,
![]() (3)
Используя
формулу (3), теорему Гаусса (2) можно
записать так:
(3)
Используя
формулу (3), теорему Гаусса (2) можно
записать так:
![]()
