- •22. Барометрическая формула. Распределение Больцмана.
- •24. Первый закон термодинамики
- •25. Второй закон термодинамики
- •100% Энергии не может быть преобразовано в работу
- •26. Третье начало термодинамики может быть сформулировано так:
- •27. Закон Кулона и напряженность электростатического поля.
- •28. Потенциал электростатического пoля.
- •29. Связь силовой и энергетической характеристик электрического поля.
- •30. Теорема Остроградского - Гаусса для поля в вакууме.
28. Потенциал электростатического пoля.
Потенциал электрического поля представляет собой отношение потенциальной энергии к заряду. Как известно электрическое поле является потенциальным. Следовательно, любое тело находящиеся в этом поле обладает потенциальной энергией. Любая работа, которая будет совершаться полем, будет происходить за счет уменьшения потенциальной энергии.
![]()
Формула 1 — Потенциал
Потенциал электрического поля это энергетическая характеристика поля. Он представляет собой работу которую нужно совершить против сил электрического поля для того чтобы переместить единичный положительный точечный заряд находящийся на бесконечности в данную точку поля.
Измеряется потенциал электрического поля в вольтах.
В случае если поле создается несколькими зарядами, которые расположены в произвольном порядке. Потенциал в данной точке такого поля будет представлять собой алгебраическую сумму всех потенциалов, которые создают заряды каждый в отдельности. Это так называемый принцип суперпозиции.
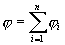
Формула 2 — суммарный потенциал разных зарядов
Допустим, что в электрическом поле заряд перемещается из точки "a" в точку "b". Работа совершается против силы электрического поля. Соответственно потенциалы в этих точках будут отличаться.
Разность потенциалов двух точек поля будет равна одному Вольту, если для того чтобы переместить заряд в один кулон между ними необходимо совершить работу в один джоуль.
Если заряды имеют одинаковые знаки, то потенциальная энергия взаимодействия между ними будет положительна. В этом случае заряды отталкиваются друг от друга.
Для разноименных зарядов энергия взаимодействия будет отрицательна. Заряды в этом случае будут, притягивается друг к другу
29. Связь силовой и энергетической характеристик электрического поля.
Будем
искать, каким образом связаны напряженность
электростатического поля, которая
является его силовой характеристикой,
и потенциал, который есть его энергетическая
характеристика поля.
Работа
по перемещению единичного точечного
положительного электрического заряда
из одной точки поля в другую вдоль оси
х при условии, что точки расположены
достаточно близко друг к другу и x2—x1=dx,
равна Exdx. Та же работа равна φ1—φ2=dφ.
Приравняв обе формулы, запишем
![]() (1)
где
символ частной производной подчеркивает,
что дифференцирование осуществляется
только по х. Повторив эти рассуждения
для осей у и z, найдем вектор Е:
(1)
где
символ частной производной подчеркивает,
что дифференцирование осуществляется
только по х. Повторив эти рассуждения
для осей у и z, найдем вектор Е:
![]() где i, j, k —
единичные векторы координатных осей
х, у, z.
Из определения градиента
следует, что
где i, j, k —
единичные векторы координатных осей
х, у, z.
Из определения градиента
следует, что
![]() или
или ![]() (2)
т.
е. напряженность Е поля равна
градиенту потенциала со знаком минус.
Знак минус говорит о том, что вектор
напряженности Е поля направлен
в сторону уменьшения потенциала.
Для
графического представления распределения
потенциала электростатического поля,
как и в случае поля тяготения,
пользуютсяэквипотенциальными
поверхностями — поверхностями, во
всех точках которых потенциал φ имеет
одинаковое значение.
Если поле
создается точечным зарядом, то его
потенциал, согласно формуле потенциала
поля точечного заряда, φ=(1/4πε0)Q/r .Таким
образом, эквипотенциальные поверхности
в данном случае — концентрические сферы
с цетром в точечном заряде. Заметим
также, линии напряженности в случае
точечного заряда — радиальные прямые.
Значит, линии напряженности в случае
точечного зарядаперпендикулярны эквипотенциальным
поверхностям.
Линии напряженности
всегда перпендикулярны к эквипотенциальным
поверхностям. В самом деле, все точки
эквипотенциальной поверхности обладают
одинаковым потенциалом, поэтому работа
по перемещению заряда вдоль этой
поверхности равна нулю, т. е.
электростатические силы, которые
действуют на заряд, всегда направлены
по перпендикурярам к эквипотенциальным
поверхностям. Значит, вектор Е всегда
перпендикулярен к эквипотенциальным
поверхностям, а поэтому линии
вектора Е перпендикулярны этим
повер¬хностям.
Эквипотенциальных
поверхностей вокруг каждого заряда и
каждой системы зарядов можно провести
бесконечное множество. Но обычно их
проводят так, чтобы разности потенциалов
между любыми двумя соседними
эквипотенциальными поверхностями были
равны друг другу. Тогда густота
эквипотенциальных поверхностей наглядно
характеризует напряженность поля в
разных точках. Там, где гуще расположены
эти поверхности, напряженность поля
больше.
Значит, зная расположение
линий напряженности электростатического
поля, можно нарисовать эквипотенциальные
поверхности и, наоборот, по известному
нам расположению эквипотенциальных
поверхностей можно найти в каждой точке
поля направление и модуль напряженности
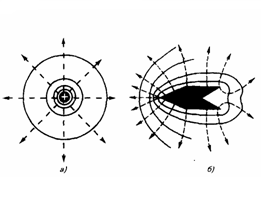
поля. На рис. 1 в качестве примера показан
вид линий напряженности (штриховые
линии) и эквипотенциальных поверхностей
(сплошные линии) полей положительного
точечного электрического заряда (а) и
заряженного металлического цилиндра,
который имеет на одном конце выступ, а
на другом — впадину (б).
(2)
т.
е. напряженность Е поля равна
градиенту потенциала со знаком минус.
Знак минус говорит о том, что вектор
напряженности Е поля направлен
в сторону уменьшения потенциала.
Для
графического представления распределения
потенциала электростатического поля,
как и в случае поля тяготения,
пользуютсяэквипотенциальными
поверхностями — поверхностями, во
всех точках которых потенциал φ имеет
одинаковое значение.
Если поле
создается точечным зарядом, то его
потенциал, согласно формуле потенциала
поля точечного заряда, φ=(1/4πε0)Q/r .Таким
образом, эквипотенциальные поверхности
в данном случае — концентрические сферы
с цетром в точечном заряде. Заметим
также, линии напряженности в случае
точечного заряда — радиальные прямые.
Значит, линии напряженности в случае
точечного зарядаперпендикулярны эквипотенциальным
поверхностям.
Линии напряженности
всегда перпендикулярны к эквипотенциальным
поверхностям. В самом деле, все точки
эквипотенциальной поверхности обладают
одинаковым потенциалом, поэтому работа
по перемещению заряда вдоль этой
поверхности равна нулю, т. е.
электростатические силы, которые
действуют на заряд, всегда направлены
по перпендикурярам к эквипотенциальным
поверхностям. Значит, вектор Е всегда
перпендикулярен к эквипотенциальным
поверхностям, а поэтому линии
вектора Е перпендикулярны этим
повер¬хностям.
Эквипотенциальных
поверхностей вокруг каждого заряда и
каждой системы зарядов можно провести
бесконечное множество. Но обычно их
проводят так, чтобы разности потенциалов
между любыми двумя соседними
эквипотенциальными поверхностями были
равны друг другу. Тогда густота
эквипотенциальных поверхностей наглядно
характеризует напряженность поля в
разных точках. Там, где гуще расположены
эти поверхности, напряженность поля
больше.
Значит, зная расположение
линий напряженности электростатического
поля, можно нарисовать эквипотенциальные
поверхности и, наоборот, по известному
нам расположению эквипотенциальных
поверхностей можно найти в каждой точке
поля направление и модуль напряженности
поля. На рис. 1 в качестве примера показан
вид линий напряженности (штриховые
линии) и эквипотенциальных поверхностей
(сплошные линии) полей положительного
точечного электрического заряда (а) и
заряженного металлического цилиндра,
который имеет на одном конце выступ, а
на другом — впадину (б).