26. Третье начало термодинамики может быть сформулировано так:
«Приращение энтропии при абсолютном нуле температуры стремится к конечному пределу, не зависящему от того, в каком равновесном состоянии находится система».
или
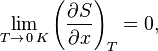
где 
—
любой термодинамический параметр.
Третье начало термодинамики относится только к равновесным состояниям.
Поскольку на основе второго начала термодинамики энтропию можно определить только с точностью до произвольной аддитивной постоянной (то есть, определяется не сама энтропия, а только её изменение):
,
третье начало термодинамики может быть использовано для точного определения энтропии. При этом энтропию равновесной системы при абсолютном нуле температуры считают равной нулю.
Третье
начало термодинамики позволяет находить
абсолютное значение энтропии, что нельзя
сделать в рамках классической термодинамики
(на основе первого и второго начал
термодинамики). В классической
термодинамике энтропия может быть
определена лишь с точностью до произвольной
аддитивной постоянной 
,
что не мешает термодинамическим
исследованиям, так как реально измеряется
разность энтропий 
в
различных состояниях. Согласно третьему
началу термодинамики, при 
значение 
.
В 1911
году Макс
Планк сформулировал
третье начало термодинамики как условие
обращения в нуль энтропии всех тел при
стремлении температуры к абсолютному
нулю: 
.
Отсюда 
,
что даёт возможность определять
абсолютное значения энтропии и
других термодинамических
потенциалов.
Формулировка Планка соответствует
определению энтропии в статистической
физике через термодинамическую
вероятность 
состояния
системы 
.
При абсолютном нуле температуры система
находится в основном квантово-механическом
состоянии. Если оно невырожденно,
то 
(состояние
реализуется единственным микрораспределением)
и энтропия 
при
равна
нулю. В действительности при всех
измерениях стремление энтропии к нулю
начинает проявляться значительно
раньше, чем могут стать существенными
дискретность квантовых уровней
макроскопической системы и влияние
квантового вырождения.
27. Закон Кулона и напряженность электростатического поля.
Закон Кулона - это закон взаимодействия двух неподвижных точечных зарядов. Закон Кулона формулируется следующим образом: Сила электрического взаимодействия между двумя точечными зарядами в вакууме пропорциональна этим зарядам и обратно пропорциональна квадрату расстояния между ними.
При взаимодействии одноименные заряды отталкиваются, разноименные притягиваются. Силы Кулона направлены по прямой, соединяющей заряды.
Закон Кулона для взаимодействия точечных зарядов Q1 и Q2, находящихся на расстоянии r друг от друга, записывается формулой:
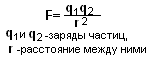
Напряженность электрического поля. Количественной характеристикой силового действия электрического поля на заряженные тела служит векторная величина E, называемая напряжённостью электрического поля.
E = F / q пр.
Она определяется отношением силы F, действующей со стороны поля на точечный пробный заряд qпр, помещенный в рассматриваемую точку поля, к величине этого заряда.
Понятие «пробный заряд» предполагает, что этот заряд не участвует в создании электрического поля и так мал, что не искажает его, т. е. не вызывает перераспределения в пространстве зарядов, создающих рассматриваемое поле. В системе СИ единицей напряженности служит 1 В / м, что эквивалентно 1 Н / Кл