21. Если газ находится в равновесии, молекулы движутся хаотически, и все направления их движения равновероятны. Скорости молекул могут быть самыми различными по модулю и при каждом соударении с другими молекулами изменяются случайным образом.

В газе, находящемся в состоянии равновесия, устанавливается стационарное распределение молекул по скоростям, подчиняющееся закону. Максвелла. Максвелл предполагал, что вещество состоит из очень большого числа тождественных молекул, находящихся в состоянии беспорядочного теплового движения при одинаковой температуре. Также предполагалось, что силовые поля на газ не действуют.

Закон Максвелла описывается некоторой функцией f(v), называемой функцией распределения молекул по модулям скоростей. Если разбить диапазон скоростей молекул на малые интервалы, равные dv, то на каждый интервал скорости будет приходиться некоторое число молекул dN(v), скорости которых заключены в этом интервале.

Функция f(v) определяет относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, то есть:

dN(v)/N=f(v)dv, откуда f(v)=dN(v)/Ndv

Применяя методы теории вероятностей, Дж. Максвелл нашел вид функции распределения молекул идеального газа по модулям скоростей хаотического движения:

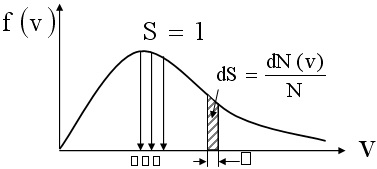  Рис. 5. График функции распределения молекул по скоростям

Выражение dN(v)/N=f(v)dv представляет собой вероятность встретить молекулу со скоростью, принадлежащей интервалу (v;v+dv). Эта вероятность равна площади заштрихованной полоски с основанием dv (рис. 5). Относительная доля молекул, имеющих определенную скорость, равна нулю.

Площадь под кривой f(v) равна вероятности достоверного события – встретить молекулу со скоростью, принадлежащей интервалу (0;∞), то есть равна единице. Это означает, что функция удовлетворяет условию нормировки:

Выражение для средней скорости <v> определяется по формуле:

<v>= vf(v)dv=√(8kT/πm₀)=√(8kN_AT/πm₀N_A)=√(8RT/πM) (32)

выражение для среднеквадратичной скорости:

<v_кв>= v²f(v)dv.

Произведя интегрирование, получим:

<v_кв>=√(3RT/M) (33)

Из функции распределения молекул по модулям скоростей можно получить функцию распределения молекул по кинетическим энергиям теплового движения:

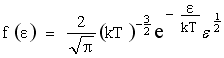
22. Барометрическая формула. Распределение Больцмана.

 При выводе основного уравнения МКТ газов и максвелловского распределения молекул по скоростям предполагалось, что на молекулы газа внешние силы не действуют, поэтому молекулы равномерно распределены по объему. Однако молекулы любого газа находятся в потенциальном поле тяготения Земли. Тяготение и тепловое движение молекул приводят к некоторому стационарному состоянию газа, при котором давление газа с высотой убывает. Больцман обобщил распределение Максвелла на случай поведения частиц в произвольном силовом поле.

Гидростатическое давление столба жидкости или газа:     ,   где   .

,   тогда          =>           =>         ;

В итоге мы получаем:      −   барометрическая формула. Барометрическую формулу можно преобразовать, если воспользоваться выражением  :

   −    распределение Больцмана во внешнем потенциальном поле. Из нее следует, что при постоянной температуре плотность газа больше там, где меньше потенциальная энергия его молекул. Если частицы имеют одинаковую массу и находятся в состоянии хаотического теплового движения, то распределение Больцмана справедливо в любом внешнем потенциальном поле, а не только в поле сил тяжести.

23. Средние скорости молекул, газа очень велики - порядка сотен метров в секунду при обычных условиях. Однако процесс выравнивая неоднородности в газе вследствие молекулярного движения протекает весьма медленно. Это объясняется тем, что молекулы при перемещении испытывают соударения с другими молекулами. При каждом соударении скорость молекулы изменяется по величине и направлению. Вследствие этого, скорость, с которой молекула диффундирует из одной части газа в другую, значительно меньше средней скорости молекулярного движения. Для оценки скорости движения молекул вводится понятие средней длины свободного пробега. Таким образом, средняя дли свободного пробега   - это среднее расстояние, которое проходит молекула от столкновения до столкновения.

Для определения   вычислим среднее число соударений   выбранной молекулы с другими молекулами за единицу времени. Будем считать, что молекула после соударения продолжает двигаться по прямой со средней скоростью движения   .

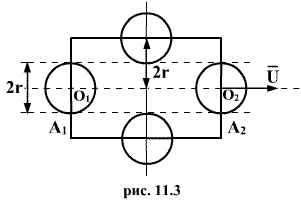
Молекулы, с которыми соударяется выбранная молекула, в первом приближении считаем неподвижными и принимаем их за сферические тела радиуса r. Пусть выбранная молекула движется вправо из положения   в положение   по прямой   (рис.11.3). Движущаяся со средней скоростью молекула в течении одной секунды столкнется со всеми молекулами, центры которых находятся в объеме ограниченном цилиндром с радиусом 2r и длиной   , т.е.

.

Если концентрация молекул n , то внутри рассмотренного цилиндра находится число молекул, равное

Это число   и определяет среднее число соударений за единицу времени.

В действительности все молекулы движутся, и возможность соударения двух частиц зависит от их относительной скорости. Поэтому вместо среднеарифметической скорости   должны входить средняя относительная скорость молекул   . Если скорости молекул распределены по закону Максвелла, то средняя относительная скорость двух молекул однородного газа в   раз превышает   . Таким образом, среднее число соударений должно быть увеличено в   раз

(11.7)

Средний путь, проходимый молекулой за единицу времени, численно равен   . Поэтому средняя длина свободного пробега равна   или

(11.8)

Таким образом, средняя длина свободного пробега   не зависит от температуры газа, т.к. с ростом температуры одновременно возрастают и   , и   . При подсчете числа соударений и средней длины свободного пробега молекул за модель молекулы было принято шарообразное упругое тело. В действительности каждая молекула представляет собой сложную систему элементарных частиц и при рассмотрении упругого соударения молекул имелось в виду, что центры молекул могут сблизиться до некоторого наименьшего расстояния. Затем возникает силы отталкивания которые вызывают взаимодействие, подобное взаимодействию при упругом ударе. Среднее расстояние между центрами молекул, взаимодействующих, как при упругом ударе, называют эффективным диаметром   . Тогда

(11.9)