5. Контрольные вопросы (тесты самопроверки)

5.1. Написать выражение для линейной модели статической системы с тремя входами и одним выходом.

5.2. Составить матрицу планирования эксперимента вида 2⁴.

5.3. Как вычисляются коэффициенты полиноминальной модели статической системы?

5.4. Почему повторные опыты позволяют уменьшить влияние случайных ошибок?

5.5. Как производится проверка модели на адекватность?

5.6. Написать выражение нерекурсивного описания динамической системы.

5.7. Найти математическую модель дискретной системы, прототипом которой является аналоговая система с импульсной реакцией g(t) = Ae^-5tsin100t.

5.8. Написать выражение рекурсивного описания динамической системы.

5.9. Найти рекурсивное выражение модели системы эквивалентной аналоговой, описываемой дифференциальным уравнением

и нарисовать схему системы.

5 .10. Рассчитать трудоемкость алгоритма вычислительного процесса, заданного графом

Трудоемкость операторов q_i = i операций, i = 1, 2, …, 8.

5.11. Определить среднее время пребывания заявки в вычислительной сети,

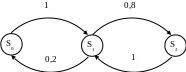
где S₁ и S₂ – одноканальные системы обслуживания со средним временем обслуживания τ₁ = 0,2 с, τ₂ = 0,6 с. Источник заявок имеет интенсивность λ₀ = 0,1 с^-1.

5.12. Оценить сравнительную производительность мультипроцессорной системы с индивидуальной памятью для каждого процессора и мультипроцессорной системы с общей памятью.

5.13. Найти рекурсивный алгоритм формирования сигнала S(t) = Ae^-5tsin100t.

5.14. Определить алгоритм формирования случайных чисел, распределенных по закону ω(y) = λe^-λy, y≥0, методом Неймана с использованием генератора стандартных случайных чисел с равномерным законом распределения.

5.15. Дать определение корреляционной функции случайного процесса и указать ее свойства.

5.16. Описать последовательность определения алгоритма формирования случайного процесса, заданного корреляционной функцией.

5.17. Нарисовать схему формирования случайного процесса.

5.18. Каковы преимущества и недостатки имитационного моделирования по сравнению с аналитическим?

5.19. Как производится описание и моделирование систем на языке GPSS?

5.20. Как производится описание и моделирование цифровых устройств на языке VHDL?

6. Теоретические сведения

Основные теоретические сведения дисциплины содержатся в учебном пособии Вишнякова В.А. Моделирование. – Рыбинск: РГАТА, 2002.

7. Указания к выполнению работы

Задания к контрольной работе содержат 10 вариантов. Каждый студент выполняет один вариант. Номер варианта соответствует последней цифре зачетной книжки.

Индивидуальное задание состоит из теоретического вопроса и двух задач.

Теория должна быть изложена компактно с полным раскрытием содержания предмета. Источником информации должны быть несколько различных книг, возможно использование сети Интернет.

Решение задач выполняется в развернутом виде.

8. Варианты заданий

Вариант 1.

1. Физическое, математическое и имитационное моделирование, построение концептуальной модели и ее формализация.

2. Построить матрицу планирования для дробного эксперимента 2⁵ и указать ее свойства.

3. Определить алгоритмы формирования случайных чисел X, плотность распределения вероятностей w(x) которых имеет вид

методами: а) функционального преобразования, б) Неймана, с использованием генератора равномерно распределенных чисел.

Вариант 2.

1. Средства моделирования и модели, применяемые в процессе проектирования вычислительных систем.

2. Нарисовать схему дискретной системы, описываемой уравнением

Y_k=a₁Y_k-1 + a₂Y_k-3 + b₁X_k-1 + b₂X_k-2,

где X_k, Y_k – входной и выходной дискретные сигналы системы, и описать как она функционирует.

3. Определить трудоемкость алгоритма вычислительного процесса, заданного следующим графом

Трудоемкость операторов равна q_i = i + 5 (операций), i = 1, 2, …, 9.

Вариант 3.

1. Моделирование статических безынерционных систем с использованием регрессионного анализа, планирование эксперимента.

2. Определить среднее время пребывания заявки в вычислительной сети, заданной графом

где S₁, S₂, S₃, S₄ – одноканальные устройства обработки со средним временем обслуживания заявок соответственно: τ₁ = 0,2 с, τ₂ = 0,6 с, τ₃ = 0,1 с, τ₄ = 0,3 с. Источник заявок S₀ имеет интенсивность λ₀ = 0,05 с^-1.

3. Определить алгоритм формирования случайной величины X, плотность распределения вероятностей w(x) которого равна

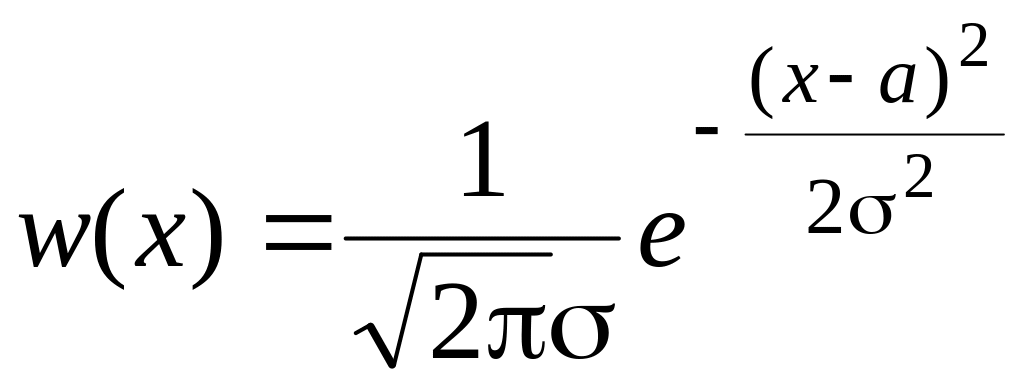
с использованием генератора равномерно распределенных случайных чисел методом Неймана.

Вариант 4.

1. Оценка точности и достоверности экспериментальных исследований при определении параметров моделей статических безынерционных систем, адекватность моделей.

2. Нарисовать схему дискретного моделирования аналоговой системы, описываемой уравнением

где X(t), Y(t) – входной и выходной сигналы системы.

3. Определить среднее время пребывания заявки в вычислительной сети заданной графом

где где S₁, S₂, S₃, – одноканальные устройства обработки со средним временем обслуживания соответственно: τ₁ = 0,01 с, τ₂ = 0,03 с, τ₃ = 0,05 с. Источник заявок S₀ имеет интенсивность λ₀ = 1 с^-1.

Вариант 5.

1. Нерекурсивные и рекурсивные модели динамических систем.

2. Проверить, есть ли грубые измерения в выборке X = (10, 15, 17, 20, 21) при пороговом уровне 1,5.

3. Определить трудоемкость алгоритма вычислительного процесса, заданного графом

Трудоемкость операторов равна q_i = i + 2 (операций), i = 1, 2, …, 7.

Вариант 6.

1. Марковские модели вычислительных процессов.

2. Проверить адекватность уравнение связи Y = 2X + 10 для статической модели системы при пороговом уровне 2, если имеются следующие статистические данные

X	0	1	2	3	4
Y	11	10	12	14	15

и среднее значение статистической дисперсии равно 1,9.

3. Найти рекуррентный алгоритм формирования сигнала S(t) = 10t sin200t. Выбрать период дискретизации.

Вариант 7.

1. Модели вычислительных систем и сетей с использованием теории массового обслуживания.

2. В результате экспериментальных исследований статической системы, имеющей 3 входных параметра (безразмерные корни равные значения X₁, X₂, X₃) и выходной Y получены следующие данные

X1	X2	X3	Y
-1	-1	+1	10
-1	+1	-1	5
+1	-1	-1	7
+1	+1	+1	8

Определить аналитическую зависимость Y = f(X₁,X₂,X₃) и преобразовать ее в зависимость – размерные входные параметры.

3. Определить рекуррентный алгоритм формирования сигнала

.

Вариант 8.

1. Статистическая имитация случайных величин, формирование случайных чисел по заданному закону распределения.

2. Определить алгоритм дискретного моделирования аналоговой динамической системы с импульсной переходной характеристикой

q(t) = Ae^-5tsin100t,

Выбрать период дискретизации.

3. Проверить на адекватность уравнение связи Y = 2X + 9 для модели статической системы при пороговом уровне 1,8 если имеются следующие экспериментальные данные

X	0	1	2	3	4
Y	8	12	13	15	17

а средняя статистическая дисперсия равна 2.

Вариант 9.

1. Цифровое моделирование детерминированных и случайных сигналов.

2. Определить алгоритм дискретного моделирования аналоговой динамичной системы с импульсной переходной характеристикой

q(t) = A₁e^-10t – A₂e^-0,1t,

Выбрать период дискретизации.

3. Определить трудоемкость алгоритма вычислительного процесса заданного графом

если трудоемкость выполнения операторов равна q_i = i (операций), i = 1, 2, …, 10.

Вариант 10.

1. Имитационное моделирование систем.

2. Определить алгоритм формирования случайных чисел X, плотность распределения вероятностей которых имеет следующий вид

методом функционального преобразования равномерно распределенных чисел.

3. Составить рекуррентное уравнение функционирования дискретной системы.