Статистический ряд вероятностей всех возможных значений при т попаданиях и остальных промахах в серии из 10 выстрелов

тi	0	1	2	3	4	5
P10(mi)	10-10	9×10-9	3,64×10-7	8,73×10-6	1,4×10-4	1,62×10-3
... mi	6	7	8	9	10
P10(mi)	1,13×10-2	5,82×10-2	0,196	0,393	0,35

Если сложить все вероятности событий, то получим åР₁₀(m) = 1, т.е. имеем полную группу событий Изобразим графически полученный статистический ряд. Такой график называется полигоном или многоугольником распределения вероятностей.

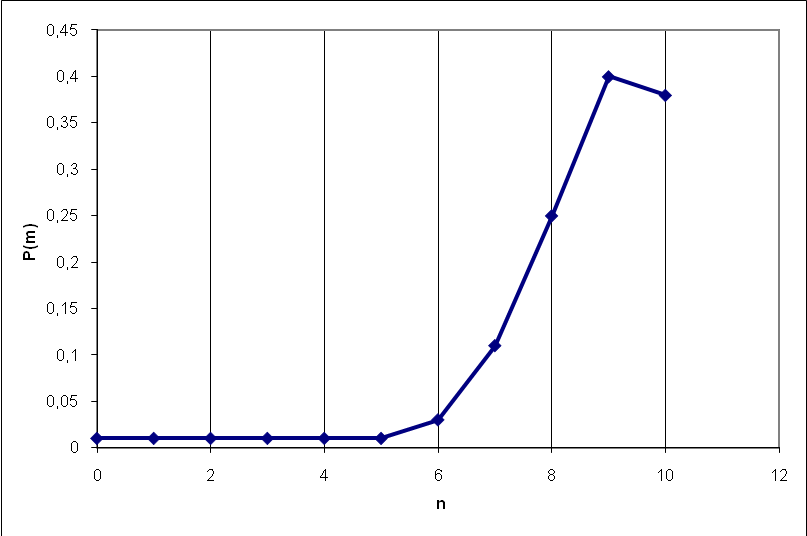
Рис. 3.1. Полигон распределения вероятностей биноминального закона при n=10, p=0.9, q=0.1.

Определение. Распределение вероятностей, определяемое формулой Бернулли (2,1), называется биномиальным распределением вероятностей дискретной случайной величины. Это название связано с тем, что формула Бернулли очень похожа на бином Ньютона. Иногда этот закон называют альтернативным, поскольку его элементарные исходы – противоположные события, отвечающие принципу «да-нет».

Математическое ожидание и дисперсия, их свойства

Определение: Математическим ожиданием дискретной случайной величины Х называется сумма произведений каждого ее значения на свою вероятность (или на практике на относительную частоту появления этого значения):

(3.5)

Знак М есть оператор, который «командует», что надо сделать со стоящей справа от него случайной величиной Х. Он означает, что нужно взять 1-е значение случайной величины и умножить его на частоту р₁ (в идеале – на вероятность), затем сложить с аналогично полученным произведением 2-го значения на его частоту, и т.д. МХ – средневзвешенное значение случайной величины. Понятие средневзвешенности можно проиллюстрировать на следующей механической модели. Пусть х₁, х₂, ..., х_n – точки на отрезке числовой оси. В этих точках сосредоточены различные веса: р₁, р₂ ,...., р_n , причем åp = 1. Тогда МХ есть точка центра тяжести на оси.

Выясним статистический смысл оценки математического ожидания. Пусть проведено п испытаний, при которых случайная величина Х приняла т₁ раз значение х₁, т₂ раз значение х₂ и т.д., причем т₁+ т₂+.....+т_к = п. Возьмем среднюю арифметическую величину

(3.6)

Относительная частота т_i/п появления любого значения х_i случайной величины Х равна статистической вероятности появления этого значения, если п конечно. Разумеется, это случайная, т.е. неабсолютно точная величина. Если же п стремится к бесконечности, то относительная частота т_i/п стремится к некоей константе, которая в пределе стремится ко все более и более точной, устойчивой, а тем самым неслучайной величине (см. выше опыты Бюффона и Пирсона с монетой. Тогда среднее значение случайной величины в пределе совпадет с ее математическим ожиданием. Например, математическое ожидание для цифр на идеально симметричной и однородной 6-гранной кости при однократном испытании точно равно 42/6 = 7/2. Такие задачи, однако, на практике нечасты, а идеальная точность никогда не достигается из-за того, что над случайной ошибкой начинает превалировать систематическая ошибка (например, отклонение формы монеты от идеально симметричной).

Поэтому математическое ожидание МХ нужно, строго говоря, приравнивать к средней оценке с помощью волнистого знака равенства:

(3.7)

Здесь математическое ожидание приблизительно равно среднему арифметическому наблюдаемых значений случайной величины с учетом их весов, т.е. частот. Если все значения появились только по одному разу, т.е. все m_i=1, то

= (х₁+х₂+...+х_п)/п » МХ.

Свойства математического ожидания:

Пусть С – константа, т.е. неслучайная величина.

1) МС = С, т.е. математическое ожидание константы есть сама эта константа.

2) М(СХ) = СМХ (это соответствует изменению масштаба случайной величины – операция неслучайная).

3) М(Х+С) = МХ + С (например, если сместить толчковую планку при прыжках в длину, то ко всем результатам следует прибавить С).

4) М ( Х₁ + Х₂) = МХ₁ + МХ₂, если Х₁, Х₂ – независимые случайные величины (например, если суммируют результаты двух попыток при прыжках в длину, причем на каждый последующий прыжок никак не влияет исполнение предыдущего прыжка спортсменом, На практике, это, разумеется, часто бывает не так: например, прыгун потянул ногу, расстроился или же наоборот настроился на результат после беседы с тренером – это все отклонения от идеальной схемы Бернулли, способные заметно изменить константу р при каждом прыжке.

* * *

Опять вернемся к примеру со стрелками. Там все Р₁₀(m) различны для случайной величины, принимающей значения конечное число точных значений m=0,1, 2,...,10. Поэтому если взять их среднеарифметическое значение, то получим точное равенство (0+1+2+...+10):11=5,5. Это среднее далеко, однако, от истинного математического ожидания, для вычисления которого нужно учесть различные веса значений:

МХ = 0× Р₁₀(0)+1× Р₁₀(1) + ....+10× Р₁₀(10) = 9

Найдем теперь суммарную вероятность того, что в Примере 1 стрелок попадет в мишень, допустим, 7, 8 или 9 раз? Вероятности Р₁₀(7), Р₁₀(8), Р₁₀(9) надо сложить, ибо это вероятности событий, попарно несовместных в одной серии из 10 выстрелов. Так получают формулу Бернулли для интервала вероятностей при m₁ £ m < m₂:

Р_n(m₁m₂)=P_n(m₁)+P_n(m₁+1)+...+P_n(m₂-1) (3.8)

(Обычно крайнее правое значение m₂ не включают в интервал, но это не принципиально.)

* * *

Определение. Отклонением случайной величины Х называется разность Х – МХ.

Определение. Дисперсией случайной величины Х называется математическое ожидание квадрата ее отклонения:

DХ=М(Х–МХ)²= (х_i – МХ)² × p_i (3.9)

Определение. Средним квадратичным отклонением случайной величины Х называется корень квадратный из ее дисперсии.

(3.10)

По-русски дисперсия это рассеяние. Ясно, что если величина Х неслучайная, то статистических отклонений нет и DХ = 0. Обычно в статистике используют квадрат отклонения. Если суммировать сами отклонения, то положительные и отрицательные их значения компенсируют друг друга, что не позволяет видеть истинное рассеяние случайной величины. Можно возразить: не обязательно брать квадраты отклонений, можно брать отклонения по модулю. Иногда так и делают при обработке результатов измерений. Но, как мы увидим дальше, именно среднее квадратичное отклонение (СКО=s), а не модуль отклонения, входит в формулу нормального закона распределения и многих других законов распределения случайных величин.

Важным свойством СКО является его размерность, такая же, как у самой случайной величины. Дисперсия же имеет размерность квадрата случайной величины, что приводит к потере наглядности (например, если случайная величина есть расстояние в метрах, то дисперсия измеряется в м², как и площадь). В математической статистике дисперсию чаще используют в теоретических выкладках, а СКО – в практических задачах.

Свойства дисперсии:

1) Дисперсия постоянной величины равна нулю: DС = 0, так как МС=С.

2) D(СХ) = С²DХ, т. е., если выносить константу из-под оператора дисперсии, то надо возводить ее в квадрат. Это нетрудно проверить:

D(СХ)= М(СХ-М(СХ))²=М(СХ-СМХ)²=С²М(Х-МХ)²=С²DХ.

3) D(Х+С)=DХ, т.е. дисперсия не зависит от смещения случайной величины на константу. (Например, можно сдвинуть планку для отталкивания при прыжках в длину. Рассеяние длины прыжков тогда просто сместится на величину этого сдвига, однако облако рассеяния вокруг нового среднего значения – математического ожидания – не изменится ни по величине, ни по форме.)

4) D( Х₁ + Х₂) = DХ₁ + DХ₂, если Х₁, Х₂ – две независимые случайные величины.

Для вычисления дисперсии часто применяют следующую удобную формулу:

DХ= М(Х²) -(МХ)² (3.11)

Её можно вывести в качестве упражнения:

DХ=М(Х-МХ)²=М(Х²-2Х×МХ+(МХ)²)=М(Х²)-2МХ×М(МХ)+М(МХ)²=

=М(Х²)-2МХ×МХ+(МХ)²=М(Х²) - (МХ)².

Напоминаем: МХ есть константа, и потому М(МХ)=МХ.

Пример 1 со стрелком (n=10; p=0,9, см. выше). Найти дисперсию и СКО.

Решение. Можно пренебречь вкладом значений случайных величин: m=0,1,2,3,4, так как соответствующие отклонения умножаются на пренебрежимо малые вероятности (см. статистический ряд выше для этой задачи и формулу для DХ). Остальные члены дают:

DХ»(5-9)²0,0016+(6-9)²×0,011+(7-9)²×0,0582+(8-9)²×0,196+(9-9)²×0,393+

+(10-9)²×0,353=0,026+0,099+0,233+0,196+0,353»0,91;

s = » 0,95.

Таким образом, СКО в нашей задаче почти равно одному выстрелу. Забегая вперед, заметим, что по правилу трех сигм (см. Лекцию 4) вероятность попаданий в данном примере 9±3 раза составляет примерно 0,997.