1. Вычисляем матрицу смежности . Переходим к п.2.

2. Определяем локальную степень каждой вершины .

3. Выбираем строку в матрице смежности, соответствующую вершине x_s с наибольшей локальной степенью. Номер выбранной строки соответствует номеру КМ.

4. Размещаем выбранный КМ в первую позицию на КМП. Исключаем первую позицию из подмножества , а вершину x_s из подмножества .

5. Для каждого неразмещенного элемента е_j вычисляем характеристику .

6. Размещаем КМ с наибольшим значением a_j в очередную позицию из подмножества . Исключаем номер очередной занятой позиции из подмножества , а вершины x_s из подмножества .

7. Если подмножество не пусто, то переходим к п.5.

8. Конец работы алгоритма.

Задания для курсовой работы

Задание 15

Итерационный алгоритм размещения на основе парных перестановок

Замечание. Пусть для определенности в качестве критерия используется суммарная длина соединений

,

где р(j)  номер позиций для j-го конструктивного элемента р(i)  номер позиций для i-го конструктивного элемента. Обозначим p(i)=h, p(j) = k.

Алгоритм.

1. Вычислить матрицу смежности .

2. Определить локальную степень каждой вершины .

3. Выполнить начальное размещение n конструктивных модулей заданной схемы в n позиций МКП.

4. Упорядочить конструктивные элементы в соответствии с убыванием характеристики .

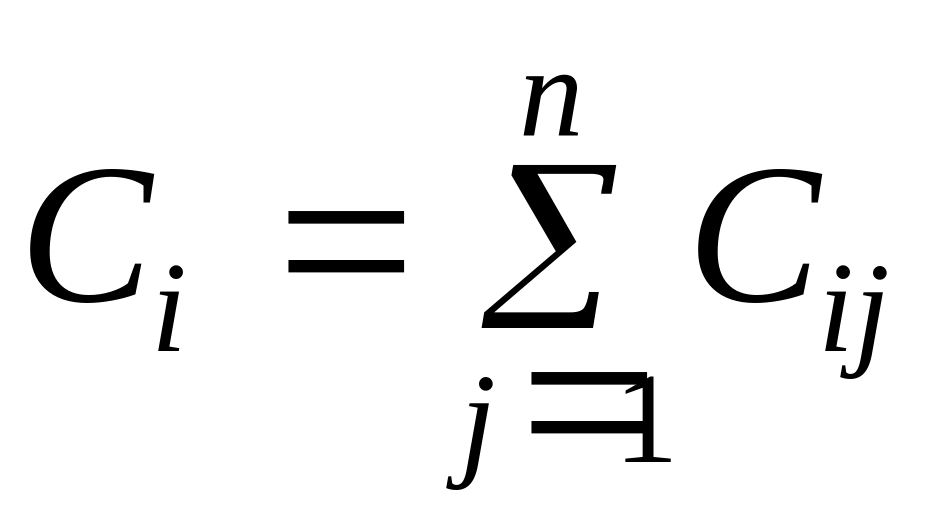
5. Выбрать очередную пару элементов е_i и e_j для возможной перестановки.

6. Вычислить значение целевой функции до перестановки местами элементов е_i и e_j ,

где D  длина соединений между элементами, не затрагиваемыми перестановкой е_i и e_j.

7. Вычислить значение целевой функции после возможной перестановки e_i и e_j местами

.

8. Вычислить приращение значения целевой функции в результате перестановки

F .

9. Выбрать из всех значений 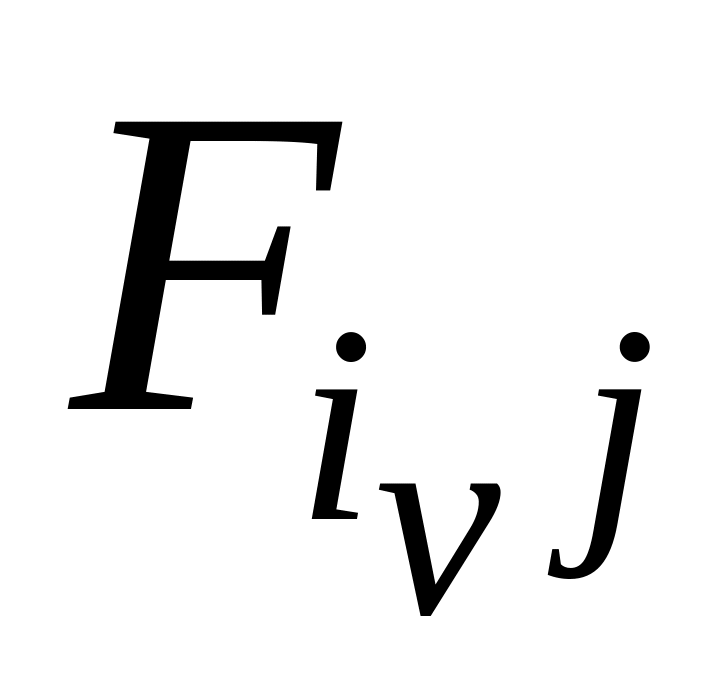 >0 наибольшее положительное и переставить местами элементы e_i и e_j. В матрице смежности i-я и j-я строки и столбцы поменяются местами. Если для некоторого элемента 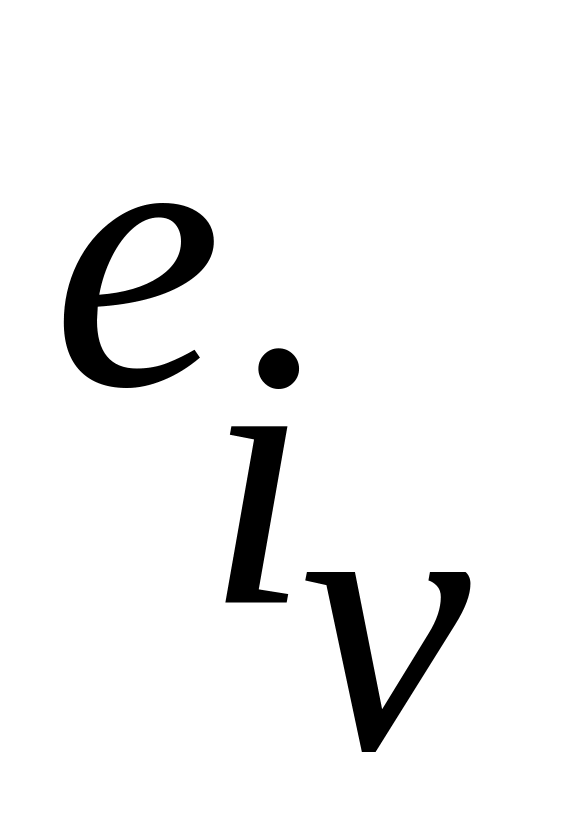не окажется приращения  >0, то этот элемент останется на месте.

10. Если ещё не все перестановки осуществлены, то переход к п.5.

11. Конец работы алгоритма.

Задания для курсовой работы

Задание 16

Алгоритм парных перестановок

Замечание. При решении задачи размещения могут появиться связи, длина которых превышает критическую.

Введем матрицу , в которой

где c_ij – элементы матрицы смежности .

Введем множество перестановочных матриц {X}: , для которых

В данных матрицах номер строки – это номер элемента, а номер столбца – это номер позиции.

Сформулируем задачу размещения следующим образом: найти перестановочную матрицу, для которой имеет место

.

Алгоритм.

1. Найти элемент e_i со связью максимальной длины.

2. Найти другой элемент e_j такой, что перестановка пары e_i и e_j местами уменьшает число связей максимальной длины и не приводит к образованию еще более длинных связей. Таких элементов может быть больше одного.

3. Среди всех элементов e_j, отобранных во втором пункте, выбрать такой элемент e_j*, что перестановка пары e_ie_j* ликвидирует наибольшее число связей максимальной длины. Осуществить такую перестановку.

4. Повторять п.п. 1  3 до тех пор, пока либо не исчезнут все связи максимальной длины (в этом случае переход к п. 5), либо ни одна из допустимых перестановок не уменьшит число связей максимальной длины. В этом случае переход к п.6.

5. Рассмотреть следующую по длине наибольшую связь и перейти к п. 1.

6. Конец работы алгоритма.

Задания для курсовой работы

Задание 17

Алгоритм построения кратчайшего покрывающего дерева Прима

Замечание. В выбранной метрике создается матрица расстояний R= между точками x_iX. При этом

Алгоритм.