Метод обратного размещения

Замечание. Предварительно оценивается каждый из элементов e₁,e₂,…,e_n и каждая из позиций: S₁, S₂,…,S_n . Затем все элементы размещаются одновременно.

Дано: матрица смежности С=║С_ij║_nn и матрица расстояний R=║r_ij|| _nn .

Для каждой строки матрицы смежности вычисляется оценка C_i= (i= ), а для каждой позиции  характеристика (i= ) – сумма расстояний от i-й позиции до остальных позиций. Очевидно, что позиции в центральной части коммутационного поля имеют меньшую характеристику r_i, чем позиция на периферии платы. Поэтому естественно, что позиции в центральной части наиболее благоприятны для размещения сильно связанных элементов.

Размещение элементов е_i (i= ) в позиции S_j (i= ) представляет собой некоторую перестановку Р(1),Р(2),…,Р(n), где Р(i) – номер позиции, присвоенной i-у элементу. Рассмотрим векторы =(С₁,С₂,…,С_n) и =(r₁,r₂,…,r_n) и их скалярное произведение .

Свойство на множестве всех перестановок Р соответствует расположению составляющих вектора по возрастанию, а составляющих вектора по убыванию.

Алгоритм.

1. Упорядочиваются элементы е_i (i= ) по возрастанию характеристики

С_i: i₁,i₂,…,i_n (C_i1 C_i2 … C_in ).

2. Упорядочиваются позиции S_j по убыванию характеристики_.

r_j : j₁,j₂,…,j_n (r_j1 r_j2 …r_jn).

3. Определяется размещение P(i_)= j_ (= ).

4. Конец работы алгоритма.

Задания для курсовой работы

Задание 24

Матричные схемы выбора размещения

Замечание. Основой для выбора элемента е_i и позиции s_j на k-м шаге размещения служит специальная матрица назначения , где а_ij представляет собой цену назначения элемента е_i в позицию s_j при условии, что (к-1)-й элемент уже размещен.

Алгоритм ( принцип максимина).

1. Для каждой строки матрицы А определяется наименьший элемент .

2. Для каждого столбца матрицы А определяется наименьший элемент .

3. Номер размещаемого конструктивного элемента и номер позиции под этот конструктивный элемент определятся элементом матрицы А, для которого имеет место .

4. Удаляется из матрицы А строка i_o (номер элемента) и столбец j_o (номер установочного места).

5. Пересчитывается цена назначения а_ij в матрице А. Она определяется как приращение целевой функции при установке каждого неразмещенного элемента e_i  в каждую незанятую позицию s_jS_к.

6. Определяется, все ли конструктивные элементы размещены. Если нет, то переход к п.1.

7. Конец работы алгоритма.

Задания для курсовой работы

Задание 25

Алгоритм минимизации числа изгибов соединений

Замечание. Критерий минимизации числа изгибов соединений важен при ортогональной трассировке. Такая трассировка возникает при конструировании двухслойных коммутационных схем, в которых горизонтальные и вертикальные отрезки соединений располагаются в разных слоях, а их электрический контакт обеспечивается специальными технологическими переходами. Определим расстояние между позициями следующим образом

Обозначим M_ih – число соединений элемента e_i с элементами, стоящими в h-м горизонтальном ряду, а N_ik – число соединений элемента e_i с элементами, стоящими в k-м вертикальном ряду,  - контактный переход.

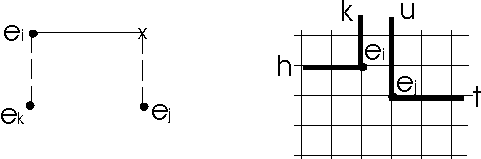
Алгоритм.

1. Поставим элемент e_i в позицию, которую занимает элемент e_j.

2. Вычислим приращение целевой функции F

 ,

где H = 2, если r_ij=1, H = 1, если r_ij=0.

3. Поставим элемент e_j в позицию, которую занимает элемент e_i.

4. Вычислим приращение целевой функции F

 .

5. Вычислим приращение целевой функции F при смене местами пары е_ie_j

 .