Построение векторной диаграммы.

Задаемся масштабом по току, например, m_i = 0,001 А/см, и по напряжению m_u = 1 B/см.

В масштабе тока откладываем вектора токов İ₁, İ₂, İ₃ под углами соответственно ψ₁=-8,26^о, ψ₂=24,3^о, ψ₃=-38,03^о к действительной оси.

Строим векторную диаграмму напряжений по контуру :

Откладываем вектор напряжения , совпадающий по фазе с током İ₁, из конца вектора строим вектор напряжения , опережающий по фазе ток İ₁ на 90^о. С вектором суммируем вектора напряжений , совпадающие по фазе с током İ₃. Сумма всех этих напряжений дает напряжение на входе цепи .

Построим диаграмму напряжений вдоль контура, содержащего . В этом случае к вектору прибавляем вектор напряжения , отстающий на 90^о от вектора тока İ₂, и из конца вектора строим вектор напряжения , совпадающий по фазе с током İ₂. В результате получим напряжение на входе цепи . При этом сумма векторов равна сумме векторов .

Векторная диаграмма представлена на рис. 3.2.2.

3.2. Пример расчета коэффициентов четырехполюсника

Ч етырехполюсник нагружен на сопротивление Z_H = 1,06 e ^j45° Ом, сопротивления четырехполюсника: Z₁ = j∙2 Ом; Z₂ = 2 Ом ; Z₃ = - j∙2 Ом. Входное напряжение U₁ = 10 B

1. Найти коэффициенты уравнений Z формы.

2. От этих коэффициентов перейти к А форме.

Решение

1. Коэффициенты уравнений Z формы.

Уравнения четырехполюсника в Z форме имеют вид

, ,

Воспользуемся опытом холостого хода со стороны вторичных зажимов, тогда , откуда:

, .

, .

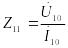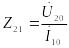Из этих уравнений видно, что коэффициент представляет собой входное сопротивление четырехполюсника по отношению к зажимам 1-1’ при холостом ходе

получаем, что

.

Найдем Z₂₁.

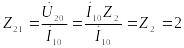Ом.

Так как при холостом ходе ,

Для определения Z₂₁ и Z₂₂ составим уравнение по 2-му закону Кирхгофа:

,

где , следовательно:

или .

т.к. , то Ом,

а

Найдем Z₁₂:

,

по аналогии с получим:

Ом

3. Перейдем к коэффициентам А формы.

Z - форма А - форма

Из второго уравнения Z - формы выразим :

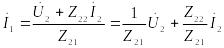отсюда:

; ;

;

Подставим полученное выражение в первое уравнение Z – формы:

тогда:

;

3.3. Примеры расчета переходных процессов.

Рассмотрим методику расчета переходных процессов на примере цепи, представленной на рис. 3.4.1.

Параметры цепи:

U = 220 B

R₁ = 50 Ом

R₂ = 80 Ом

L = 100 мГн =10^-1 Гн

С = 2 мкФ = 2·10^-6 Ф

Рис.3.4.1

Требуется определить закон изменения тока в неразветвленной части цепи при включении цепи на постоянное напряжение.