Контрольные вопросы

1. Какие цепи называют дифференцирующими? Нарисуйте схемы пассивных диф­ференцирующих цепей на основе емкостного и индуктивного элемента. Какие требования предъявляются к параметрам этих цепей?

2. Можно ли построить пассивную цепь, которая осуществляет дифференцирование абсолютно точно? Почему?

3. Какие цепи называют интегрирующими? Нарисуйте схемы пассивных интегри­рующих цепей на основе емкостного и индуктивного элемента Какие требования предъявляются к параметрам этих цепей?

4. Можно ли построить пассивную цепь, которая осуществляет интегрирование аб­солютно точно? Почему?

5. Влияет ли постоянная составляющая входного сигнала на выходной сигнал дифференцирующей цепи? Влияет ли постоянная составляющая входного сиг­нала на выходной сигнал интегрирующей цепи? Почему?

Лабораторная работа № 6 исследование длинных линий

Цель работы: изучить распределение напряжения в длинных линиях; эксперимен­тально исследовать прохождение сигналов через линию задержки в виде искусст­венной длинной линии.

Краткие теоретические сведения

В цепях, размеры которых соизмеримы с длиной волны λ, которая распро­страняется по этим цепям, необходимо учитывать, что электрическое и магнитное поля, распределены по всем участкам цепи, так же как по всем участкам происходит превращение электромагнитной энергии в тепловую. Такие цепи называют цепями с распределенными параметрами. К ним относятся линии электропередачи длиной десятки километров и более, линии связи, многие радиотехнические устройства и их отдельные узлы. Эти цепи называют еще длинными линиями (исторически первыми цепями с распределенными параметрами были именно линии связи и линии элек­тропередачи большой длины), но следует помнить, что «длинные линии» действи­тельно являются длинными (в обычном понимании) только для низких частот. При высоких же частотах, характерных для многих радиотехнических устройств, длина волны измеряется не сотнями километров, а метрами или долями метра. Практиче­ски длинными обычно считают линии, у которых геометрическая длина l ≥ 0.05λ; естественно, такой критерий является достаточно условным и может при необходи­мости корректироваться.

В противоположность цепям с распределенными параметрами (длинным ли­ниям) цепи, размеры которых много меньше длины волны, называют цепями с со­средоточенными параметрами. Ранее нами рассматривались именно такие цепи. При этом считалось, что в цепи магнитному полю, электрическому полю и потерям на тепло, а значит и связанным с ними параметрам цепи R, L, С, отводится опреде­ленное место,

Строго говоря, термины «цепь с распределенными параметрами», «длинная линия» и «цепь с сосредоточенными параметрами» применимы только к идеализи­рованным (моделирующим) цепям и не должны использоваться для характеристики реальных цепей. Тем не менее, эти термины часто применяют к реальным цепям, подразумевая, что реальные цепи достаточно адекватно описываются соответст­вующей моделирующей цепью.

Рассмотрим двухпроводную линию передачи (рис. 6.1). Обычно (для цепей с сосредоточенными параметрами) считается, что ток и напряжение вдоль линии не изменяются (т.е. , ). Однако в реальной линии всегда существует некоторая утечка тока из-за имеющейся между проводами емкости (токи смещения) и из-за несовершенства изоляции (токи утечки); для длинных линий эти эффекты следует учитывать. Поэтому для цепей с распределенными параметрами токи в проводах нельзя считать н еизменными вдоль линии: их величина в раз­ных точках линии различна.

Кроме того, токи вызывают падение напряжения на активном сопротивлении проводов линии и создают вокруг проводов переменное магнитное поле, которое наводит в проводах ЭДС самоиндукции, на преодоление которой также затрачивается на­пряжение. Следовательно, напряжение между проводами будет изменяться вдоль линии.

Таким образом, ток и напряжение в цепях с распределенными параметрами являются функциями двух переменных - времени и пространственной координаты (расстояния от начала или от конца линии).

Чтобы учесть изменения напряжения и тока вдоль линии, нужно разбить ли­нию на бесконечно малые элементы dx и считать, что каждый из них обладает ак­тивным сопротивлением R, индуктивностью L , а между проводами - активной про­водимостью G и емкостью С, то есть считать параметры, характеризующие линию, распределенными вдоль всей ее длины. Отсюда и название - цепи с распределен­ными параметрами. Внутри же каждого элемента параметры можно считать сосре­доточенными.

Если параметры R, L, G и С равномерно распределены вдоль линии, то такую линию называют однородной. Обычно линия характеризуется параметрами, отнесенными к единице ее длины (погонными параметрами).

Первичными параметрами линии являются R₀, L₀, G₀, С_0. Эти параметры обусловлены конструктивными особенностями линии.

Здесь R₀ и L₀ – продольные параметры.

R₀ – активное сопротивление, обусловленное тепловыми потерями в проводах и поверхностными эффектами.

L₀ – индуктивность цепи, определяемая магнитным потоком, который сцепляется с контуром тока, образуемым токоведущими проводами.

G₀ и С₀ – поперечные параметры линии.

G₀ – поперечная проводимость или проводимость утечки, вызванная несовершенством изоляции проводов, причем в данном случае G₀ ≠ R₀, так как эти параметры обусловлены различными причинами и не связаны друг с другом.

С₀ – емкость цепи, обусловленная емкостью между проводами, емкостью проводов по отношению к земле.

В зависимости от конкретных условий некоторыми параметрами иногда пре­небрегают. Например, в воздушных линиях сильного тока при отсутствии короны, обычно пренебрегают проводимостью утечки между проводами, так как ток, от­ветвляющийся из-за несовершенства изоляции, несравненно меньше рабочего тока. Если индуктивное сопротивление много больше продольного активного сопротивле­ния ( ), а емкостная проводимость много больше поперечной активной про­водимости ( ), то потерями на активных сопротивлениях и проводимостях можно пренебречь; такую линию считают линией без потерь.

Если заданы параметры длинной линии R₀, L₀, G₀ и C₀, то токи и напряжения в ней могут быть описаны дифференциальными уравнениями в частных производ­ных. Для этого, как сказано выше, следует представить длинную линию в виде мно­жества соединенных цепочкой бесконечно малых элементов длиной dx . Каждый из этих элементов имеет активное сопротивление R₀ dx, индуктивность L₀dx, проводимость утечки G₀dx и емкость C₀dx (рис. 6.2).

П риняв за начало отсчета расстояний нагрузочный конец (так как чаще из­вестны параметры потребителей) и используя законы Кирхгофа и простейшие мате­матические преобразования, можно записать основные уравнения однородной длинной линии:

Если вести отсчёт расстояний от генераторного конца, то аналогичным обра­зом можно получить основные уравнения длинной линии в несколько иной форме:

.

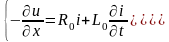B таком виде основные уравнения длинной линии часто называют телеграфными уравнениями.

Обе формы записи уравнений справедливы при любом законе изменения на­пряжения u и тока i во времени. Их решение при определённых начальных и гра­ничных условиях даёт возможность найти ток и напряжение как функции времени и расстояния,

Следует отметить, что длинной линией может быть не только двухпроводная линия, но и любая другая структура: коаксиальная линия, микрополосковая линия (специальным образом рассчитанные и выполненные проводники на печатной пла­те); более того, «длинной линией» (в данном случае правильнее сказать «цепью с распределенными параметрами») может быть на соответствующих частотах не ли­ния в обычном понимании, а, например, катушка индуктивности, проволочный рези­стор и т.п. В принципе, разновидностью длинных линий можно считать различные волноводы и большинство типов антенн, хотя обычно их рассматривают отдельно.

Каждая линия характеризуется волновым сопротивлением Z₀ и постоянной распространения γ; обе величины в общем случае комплексные.

Волновое сопротивление линии равно:

,

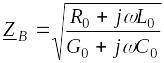для линии без потерь можно записать:

.

Постоянная распространения равна:

γ = α + јβ ,

где α - коэффициент затухания, характеризующий затухание сигнала вдоль линии (вещественная часть постоянной распространения); β - коэффициент фазы, харак­теризующий изменение фазы сигнала вдоль линии (мнимая часть постоянной рас­пространения). Для линии без потерь можно записать:

; ; ;

Входное сопротивление любой линии можно определить через входной ток и входное напряжение :

.

Электромагнитная волна распространяется вдоль линии с конечной скоро­стью:

.

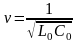Эту скорость еще называют фазовой, т.к. она представляет собой скорость переме­щения по линии неизменного фазового состояния. Следовательно, отклики в раз­личных точках длинной линии появляются не в момент подключения генератора, а несколько позже, причем время запаздывания , (время появления отклика на конце линии) зависит от длины линии l и скорости распространения волны v

Линия без потерь является идеальной линией задержки, т.к такая линия не искажает форму сигнала. Действительно, если скорость распространения волны не зависит от частоты сигнала, то все составляющие различных частот (гармонические составляющие, спектральные составляющие) любого сложного сигнала перемеща­ются с одинаковой скоростью и приходят в любую точку линии одновременно, а это означает, что форма сигнала не изменится. В общем случае - в линии с потерями -тоже возможна неискаженная передача сложного сигнала: для этого необходимо, чтобы от частоты сигнала не зависела не только скорость распространения сигнала, но и коэффициент затухания (т.е. нужно, чтобы составляющие различных частот ос­лаблялись одинаково). Скорость распространения сигнала и коэффициент затуха­ния не зависят от частоты, если для линии выполняется условие:

Как видно, линия без потерь является частным случаем линии без искажений. Однако в действительности линии без потерь не бывает, а для реальных линий вы­шеприведенное условие обычно не выполняется. Практически устранение частотных искажений во всем передаточном тракте часто достигают не за счет использования линий без искажения, а путем включения в тракт специальных корректирующих че­тырехполюсников.

Т.к. длинная линия без потерь является идеальной линией задержки, на прак­тике иногда действительно применяют линии задержки в виде отрезков коаксиально­го кабеля; известны и специально сконструированные для этой цели кабели задерж­ки. Однако геометрическая длина линий, необходимая для получения задержки все­го в единицы микросекунд, оказывается очень большой (для кабелей распростра­ненных типов требуемая длина составляет около 200 м). Поэтому в реальных уст­ройствах в качестве линий задержки часто используют искусственные длинные ли­нии, представляющие собой большое число каскадно включенных звеньев с сосре­доточенными параметрами. Чем больше звеньев имеет искусственная линия, тем ближе ее свойства к «настоящей» длинной линии, но физические процессы в этих цепях различны. В частности, время задержки для длинной линии - это время про­хождения электромагнитной волной линии, т.е. понятие «задержка» здесь использу­ется буквально. Для искусственной длинной линии, являющейся четырехполюсни­ком с сосредоточенными параметрами, время задержки - это время, отсчитываемое от момента поступления сигнала на вход линии, до момента, когда напряжение на выходе линии нарастет от нуля до некоторого определенного значения (например, до 0,5 от амплитудного) при относительно небольшом изменении формы сигнала по сравнению с входным Физически это время обусловлено переходным процессом в четырехполюснике и нагрузке. Причем неискаженная передача сложного сигнала по искусственной длинной линии, в отличие от «естественной», невозможна ни при ка­ких обстоятельствах (в том числе и теоретически).

Время задержки искусственной линии:

где L_1.. С₁- индуктивность и емкость каждого звена искусственной линии; n - число звеньев. Таким образом, искусственная линия, состоящая из η звеньев эквивалент­на двухпроводной линии с погонными индуктивностью L₀ = L₁ и емкостью С₀ = С₁ такой длины, при которой получается такое же время задержки г., как у искусствен­ной линии. Очевидно, если время задержки равно периоду сигнала, то расстояние, проходимое сигналом за это время, равно длине волны λ. Таким образом, на искус­ственной длинной линии укладывается одна длина волны сигнала частотой

,

другими словами, при этой частоте эквивалентная длина искусственной линии равна длине волны λ. Учитывая, что длина волны в свободном пространстве равна

,

где с - скорость света; для эквивалентной длины искусственной пинии можно запи­сать;

.

Если линия нагружена на сопротивление, равное волновому, то и пинии рас­пространяется только падающая волна (отраженной волны нет), такой режим назы­вают режимом бегущих волн. Если же линия нагружена на сопротивление, отличное от волнового, то в линии всегда имеется отраженная волна. Коэффициент отраже­ния по напряжению - это отношение напряжения отраженной волны в конце пинии к напряжению падающей волны в конце линии. Коэффициент отражения по напряже­нию может быть выражен через волновое сопротивление линии и сопротивление на­грузки:

,

где - сопротивление нагрузки. Коэффициент отражения по току p_i=-p, чаще пользуются коэффициентом отражения по напряжению, при этом слова «по напря­жению» обычно опускают. Если p = ±1 (амплитуда отраженной волны равна амплитуде падающей волны), то возникает режим стоячих волн, характеризующийся нали­чием узлов и пучностей напряжения и тока. Для других значений коэффициента от­ражения амплитуда отраженной волны не равна амплитуде падающей волны, такой режим называют режимом смешанных волн. Режим смешанных волн характеризуется не узлами и пучностями, а минимумами и максимумами напряжения и тока. Ко­эффициентом бегущей волны называют отношение минимума напряжения смешанной волны к ее максимуму:

.

Коэффициентом стоячей волны называют обратную величину:

.

Можно выразить коэффициент бегущей волны (и, соответственно, коэффициент стоячей волны) через волновое сопротивление линии и сопротивление нагрузки

.

В зависимости от сопротивления нагрузки можно выделить различные режи­мы работы линии:

- режим холостого хода (пиния разомкнута на конце, );

- режим короткого замыкания (линия замкнута на конце, );

- режим работы на согласованную нагрузку (линия нагружена на сопротивление нагрузки, которое равно волновому, );

- режим работы на несогласованную нагрузку (линия нагружена на сопротивле­ние нагрузки, которое не равно волновому, );

- режим работы на реактивную нагрузку (линия нагружена на индуктивный или емкостной элемент, ).

Каждый режим характеризуется различными распределениями токов и напря­жений вдоль линии. В общем случае комплексные действующие значения напряже­ния и тока в любой точке линии определяются из выражений:

;

,

где , - комплексные действующие значения напряжения и тока на расстоянии от конца линии; , 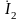- комплексные действующие значения напряжения и тока в конце линии, т.е. на нагрузке. Для линии без потерь вышеприведенные выражения примут вид:

С учетом последних выражений можно найти распределения токов и напря­жений для различных режимов работы линии без потерь.

Для режима холостого хода линия разомкнута на конце ( ), учитывая, что = 0, можно записать:

Имеет место режим стоячих волн: р_хх=1; К_{бв хх}=0; К_{св хх}=∞. На конце линии пучность напряжения и узел тока. Входное сопротивление:

;

таким образом, изменяя длину отрезка линии без потерь, можно имитировать емкостное и индуктивное сопротивления любой величины. Это свойство широко исполь­зуется в различных радиотехнических установках.

Для режима короткого замыкания линия замкнута на конце (Z_н = 0),

учитывая, что U₂= 0 , можно записать:

Имеет место режим стоячих волн: р_кз= -1; К_{бв кз} = 0 ; К_{св хкз}=∞. На конце линии узел напряжения и пучность тока. Входное сопротивление:

.

Таким образом, изменяя длину отрезка линии без потерь, также можно имитировать различные по величине емкостные и индуктивные сопротивления. В частности, от­резок короткозамкнутой на конце линии без потерь длиной в четверть длины волны имеет бесконечное сопротивление, что позволяет применять его при подвеске про­водов в качестве изолятора.

Для режима работы на согласованную нагрузку, когда линия нагружена на со­противление нагрузки, которое равно волновому ( Z_н = Z_в ), учитывая, что 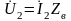можно записать:

Имеет место режим бегущих волн: ρ = 0; К_бв = 1; К_св = 1, Амплитуды напряжения и тока постоянны по всей длине линии. Входное сопротивление:

.

Для режима работы на несогласованную нагрузку, когда линия нагружена на сопротивление нагрузки, которое не равно волновому (Z_н ≠ Z_B), учитывая, что 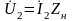, можно записать:

Имеет место режим смешанных волн:

; ; .

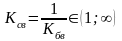Амплитуды напряжения и тока изменяются по длине линии. Входное сопротивление:

.

При нагрузке линии на элементы с чисто реактивным сопротивлением ( ) в линии имеет место режим стоячих волн, однако при этом на выходе линии нет ни узла, ни пучности напряжения (или тока), поскольку они сдвигаются вдоль линии. При индуктивной нагрузке узлы и пучности напряжения смещаются влево (в сторону генератора), а при емкостной нагрузке - вправо (в сторону нагрузки).

В линии, замкнутой на элемент с чисто реактивным сопротивлением, можно заменить этот элемент эквивалентным отрезком линии, у которого входное сопро­тивление равно сопротивлению реактивного элемента. Например, емкостной эле­мент можно заменить разомкнутым отрезком линии длиной менее четверти длины волны, а индуктивный - короткозамкнутым отрезком линии длиной менее четверти длины волны и т.д. Входное сопротивление:

,

где ; при индуктивной нагрузке:

; ; v > 0;

при емкостной нагрузке:

; ; v < 0.